Файл: Методические указания и задания к курсовому проектированию для студентов специальности Радиотехника Екатеринбург 2022 удк 621. 396.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 105
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
- необходимые сдвиги фаз между соседними элементами в строке и столбце.
Рассмотрим два частных случая, широко используемых на практике, амплитудных распределений токов в АР, для которых имеются аналитические формулы расчета ДН:
1. Закон распределения «Косинус на пьедестале»:

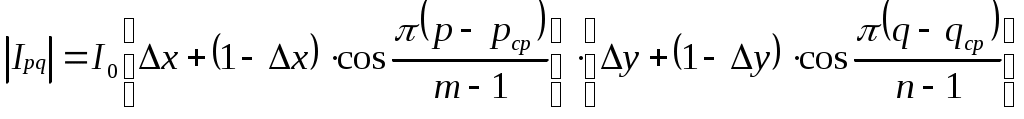 . (2.2)
. (2.2)
ДН в этом случае определяется формулой:
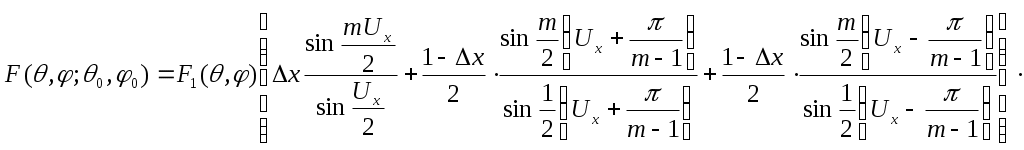
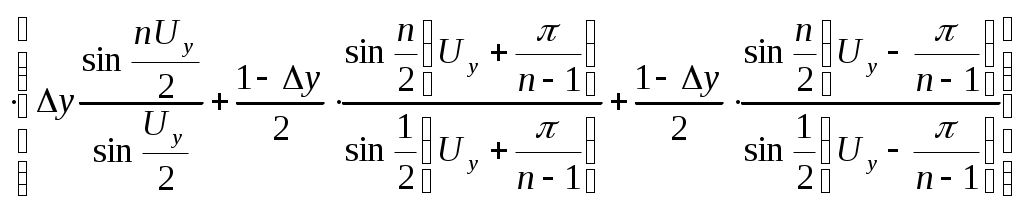 , (2.3)
, (2.3)

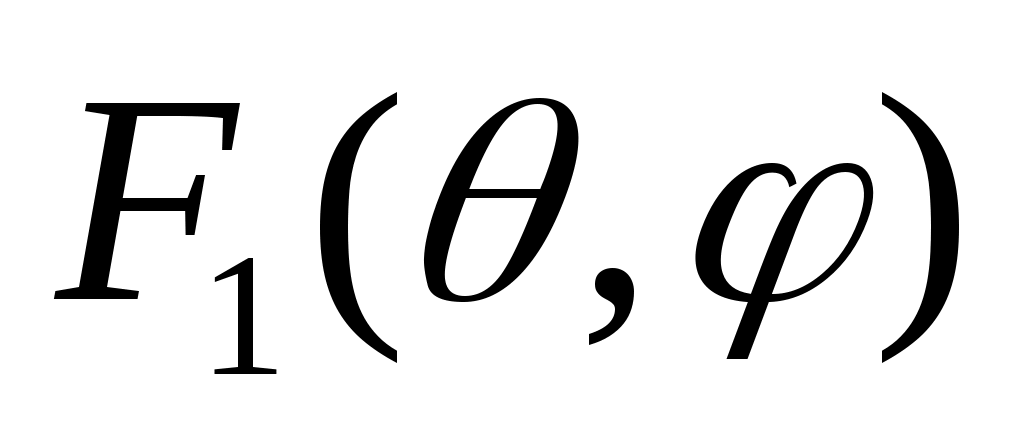 - ДН одиночного элемента.
- ДН одиночного элемента.
2. Закон распределения «Косинус квадрат на пьедестале»:
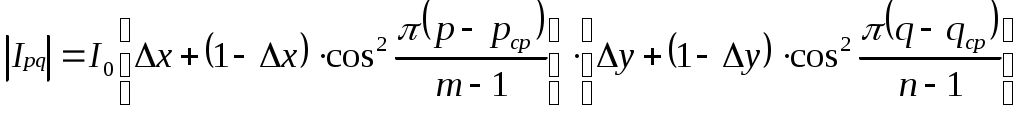 . (2.4)
. (2.4)
Выражение для ДН
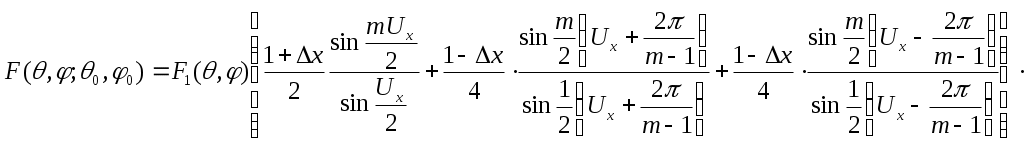
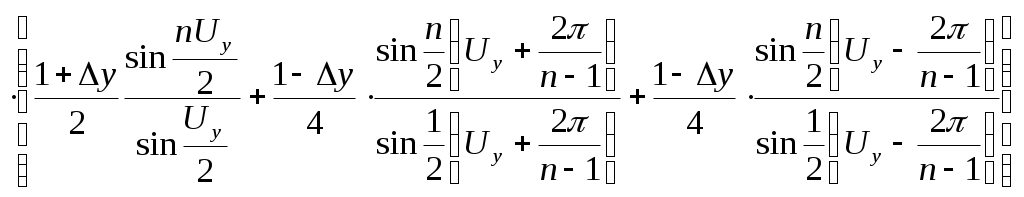 (2.5)
(2.5)
Для обоих законов распределения амплитуд
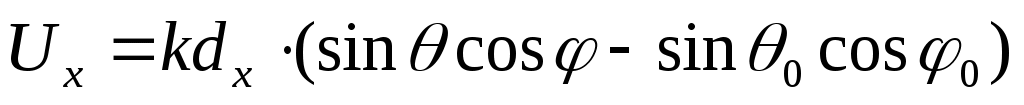 ,
,
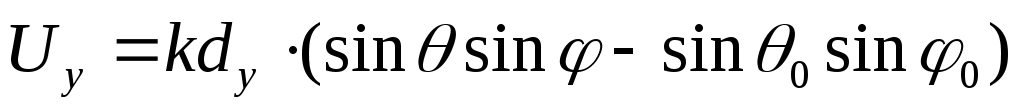 (2.6)
(2.6)
Из формулы (2.2) следует частный случай равноамплитудного распределения (Δx=Δy=1).
Для приближенной численной оценки ширины главного лепестка ДН и УБЛ при таких вариантах возбуждения можно использовать данные табл. 3.1, где приведены соотношения для прямоугольных синфазных и непрерывно возбужденных раскрывов. При этом необходимо помнить, что приведенные расчетные соотношения не учитывают направленные свойства одиночных элементов, возможность отклонения луча от нормали (несинфазное возбуждение элементов) и, что их использование возможно только при достаточно большом числе элементов в строке и столбце с выбором периода решетки в соответствии формулой 6.1.
Используя данные табл. 3.1 видно, что амплитудное распределение токов по элементам влияет на ширину главного лепестка ДН и на УБЛ. Учитывая, что ширина главного лепестка зависит ещё и от размеров решётки, выбор распределения при проектировании антенны производят по УБЛ. В последующем распределение корректируется с учетом направленности одиночных элементов и ростом УБЛ при отклонении луча от нормали.
В двумерной решетке, так же как и в линейной, происходит расширение главного лепестка ДН при отклонении луча от нормали.
Для остронаправленных решёток, у которых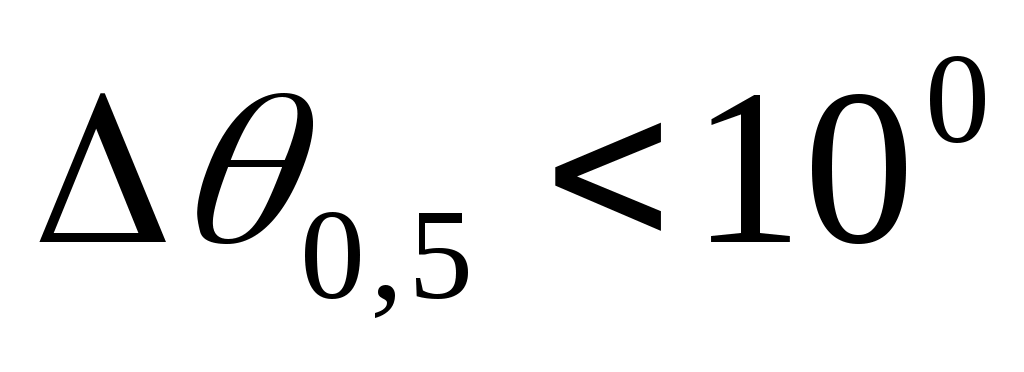 , можно считать, что расширение лепестка происходит только в плоскости сканирования. В этих случаях для ширины ДН справедливы приближенные формулы (равноамплитудные распределения):
, можно считать, что расширение лепестка происходит только в плоскости сканирования. В этих случаях для ширины ДН справедливы приближенные формулы (равноамплитудные распределения):
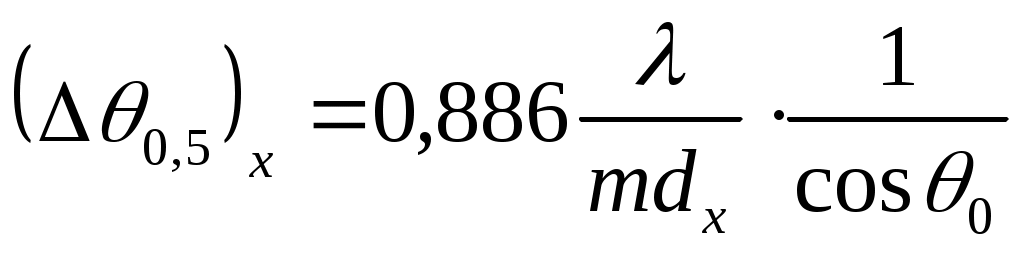 ;
; 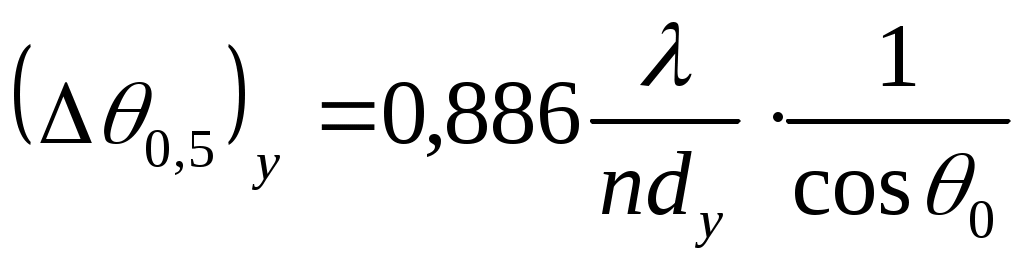 , (2.7)
, (2.7)
где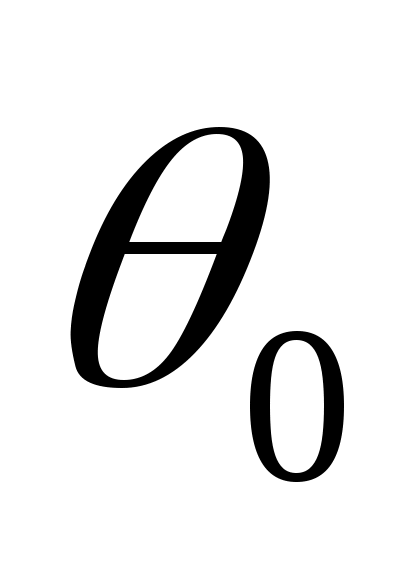 - угол отклонения луча от нормали.
- угол отклонения луча от нормали.
КНД ФАР с равномерным по амплитуде распределением определяются следующим выражением:
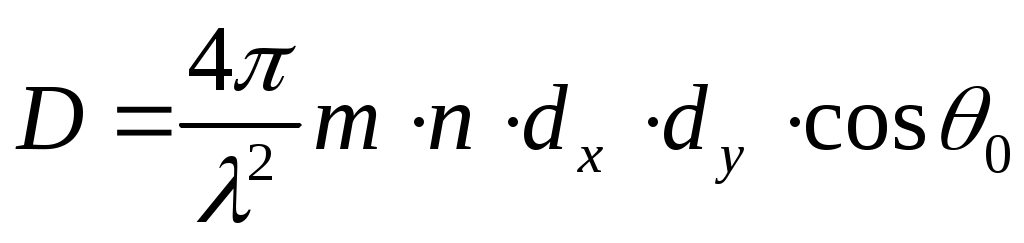 (2.8)
(2.8)
3. Рефлекторные параболические антенны
Параболические антенны используются для создания остронаправленного излучения за счет преобразования сферического фронта волны облучателя в плоский фронт после отражения ее от зеркала – рефлектора. В трактовке геометрической оптики, справедливой при больших электрических размерах зеркал, это объясняется тем, что для источника, помещенного в точке фокуса параболического отражателя, все отраженные лучи параллельны оси параболоида, а расстояние вдоль лучей от фокуса до плоскости, перпендикулярной оси, одинаковы.
Таким образом, излучение параболической антенны можно свести к излучению плоской синфазной поверхности (раскрыва) больших электрических размеров, которая, как известно, обладает высокой направленностью.
Д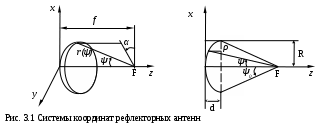 алее будут рассмотрены основные модификации рефлекторных антенн и особенности их расчета.
алее будут рассмотрены основные модификации рефлекторных антенн и особенности их расчета.
Чаще всего, рефлектор является симметричной или несимметричной вырезкой из параболоида вращения, который в прямоугольной системе координат (x, y, z) описывается уравнением:
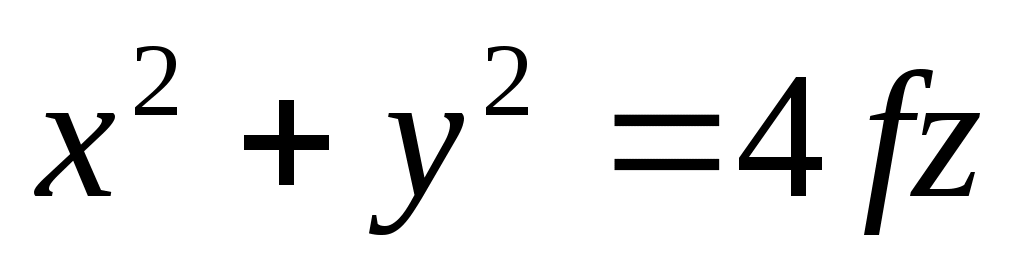 , (3.1)
, (3.1)
а в сферической (r, Ψ, α), с началом координат в фокусе параболоида:
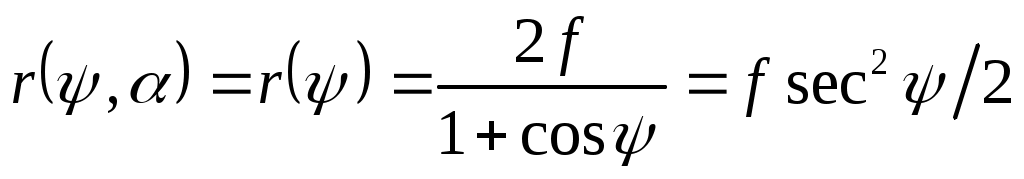 (3.2)
(3.2)
Радиус раскрыва - R, угол раскрыва - ψ0 и фокусное расстояние - fсвязаны между собой соотношениями:
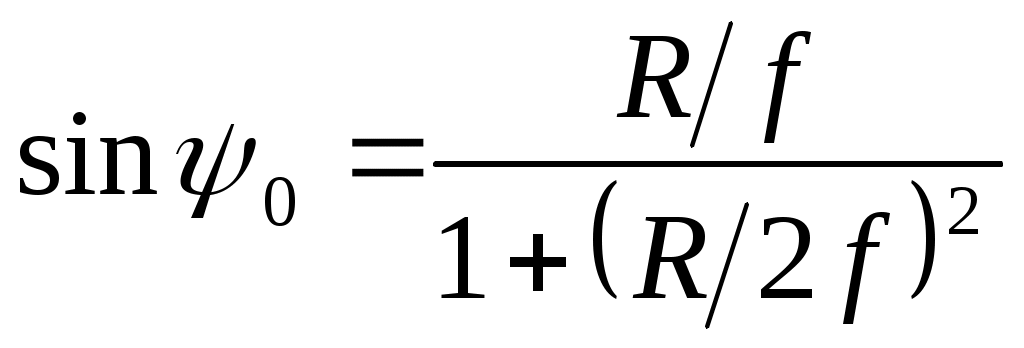 ;
; 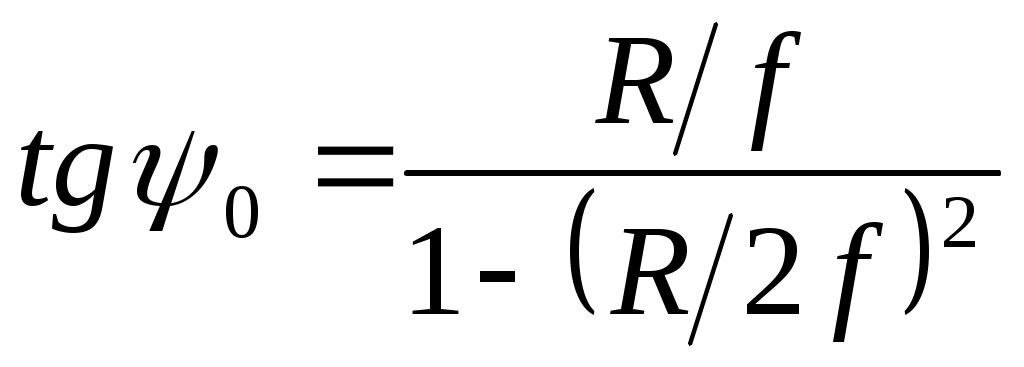 ;
; 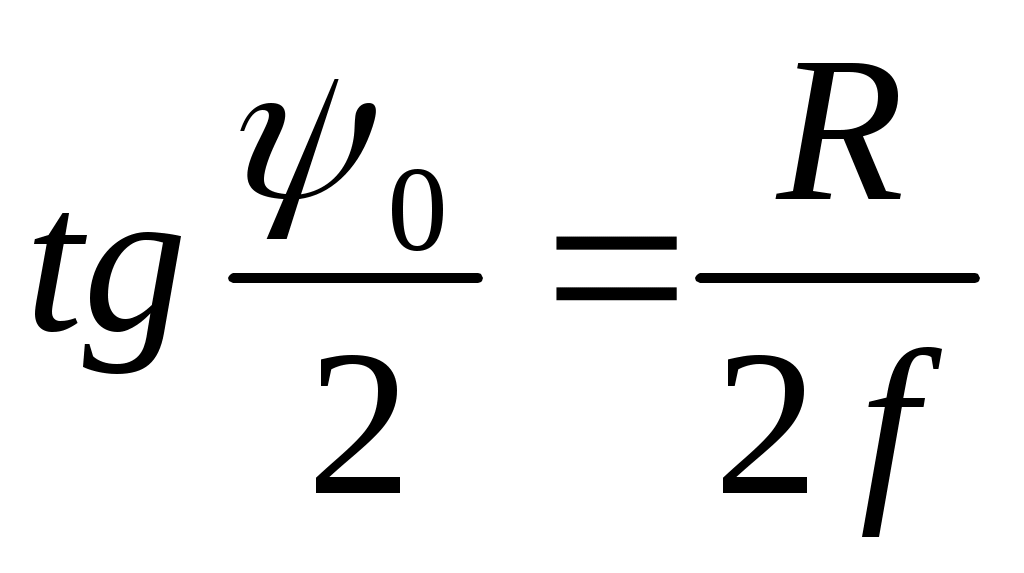 (3.3)
(3.3)
В большинстве практических случаев 45º<ψ0<90º, так что 0,4<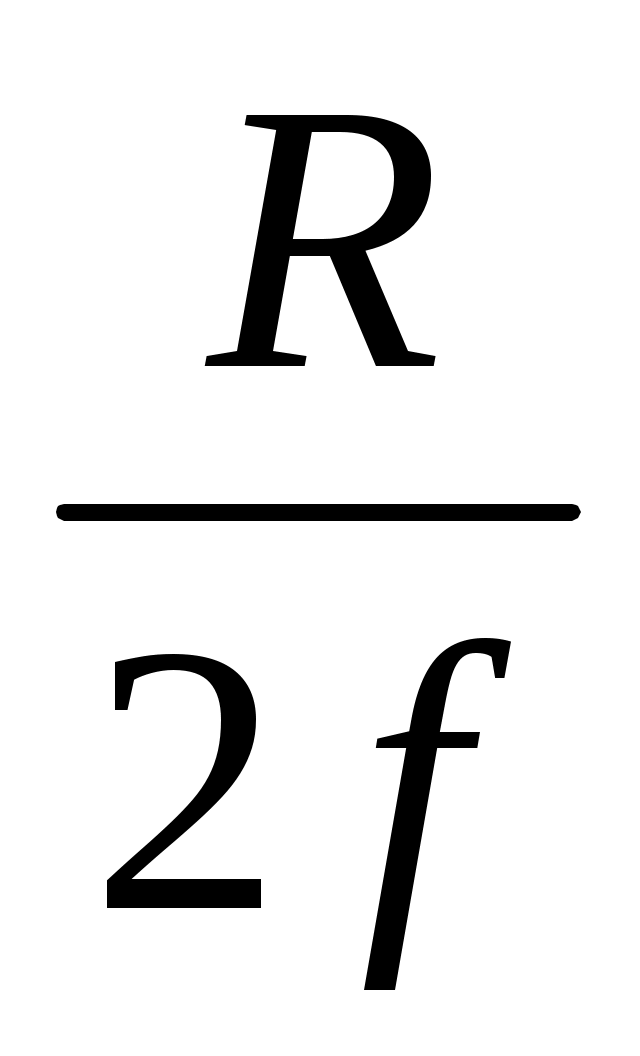 <1.
<1.
Из (3.1) легко определить глубину зеркала:
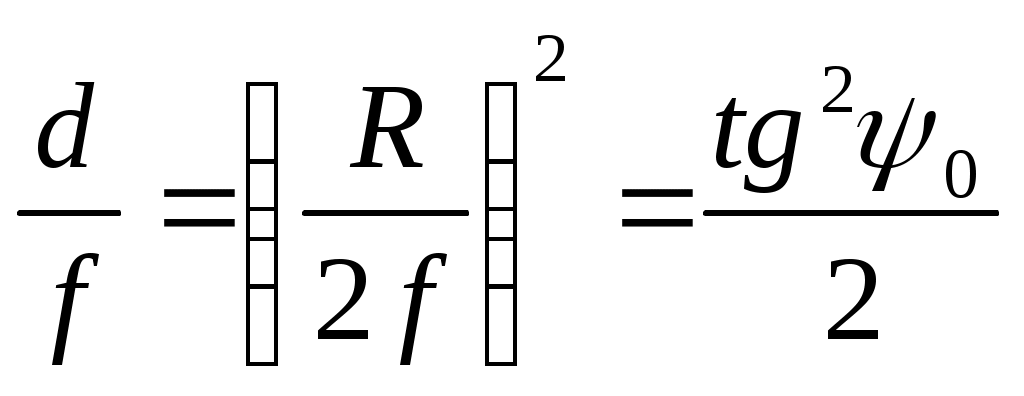 (3.4)
(3.4)
Наиболее просто направленные свойства рефлекторной антенны рассчитываются так называемым апертурным методом, т.е. по полю в ее раскрыве.
При установке в фокусе рефлектора облучателя с диаграммой направленности Fобл(ψ,α) в раскрыве зеркала наводится синфазное поле с амплитудным распределением
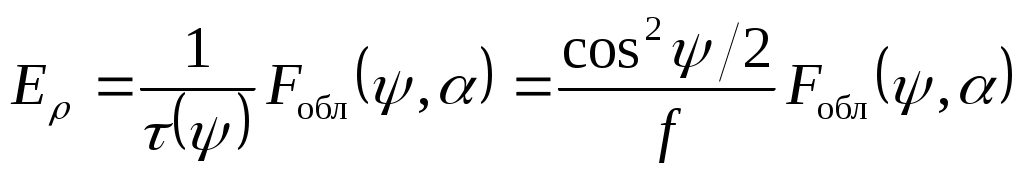 (3.5)
(3.5)
При этом координаты точек раскрыва xρ, yρ или ρρ, αρ связаны с углами ψ и α соотношениями, обусловленными геометрией задачи:
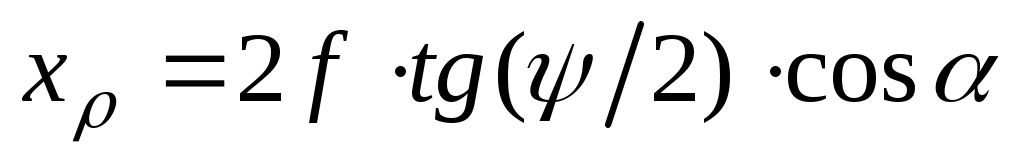 ;
;
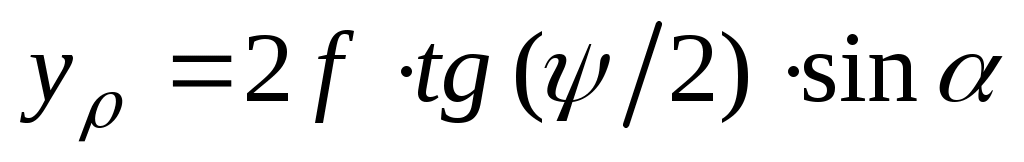 ; (3.6)
; (3.6)
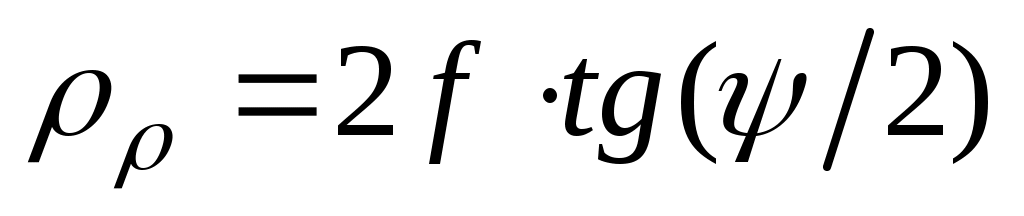 ;
; 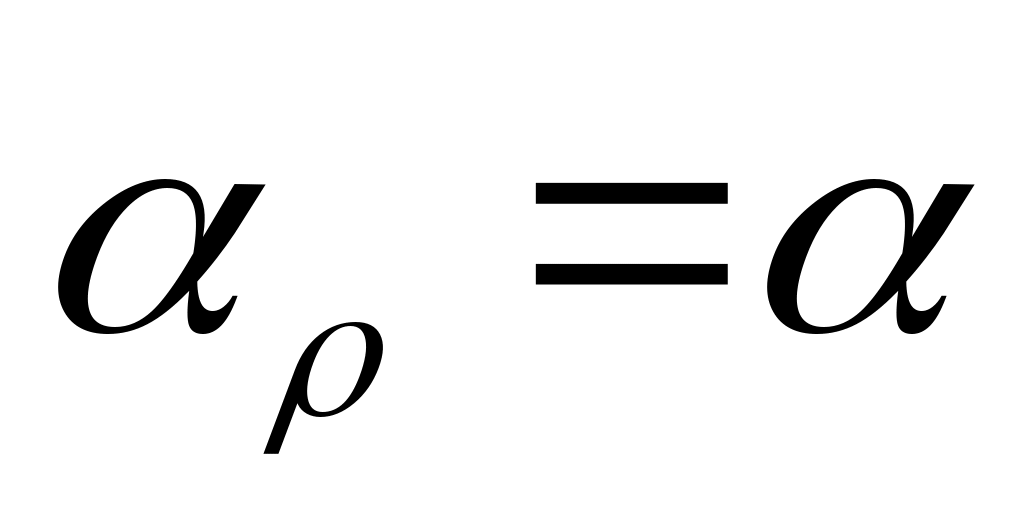
По известному полю в раскрыве рассчитывается диаграмма направленности антенны F(θ,φ):
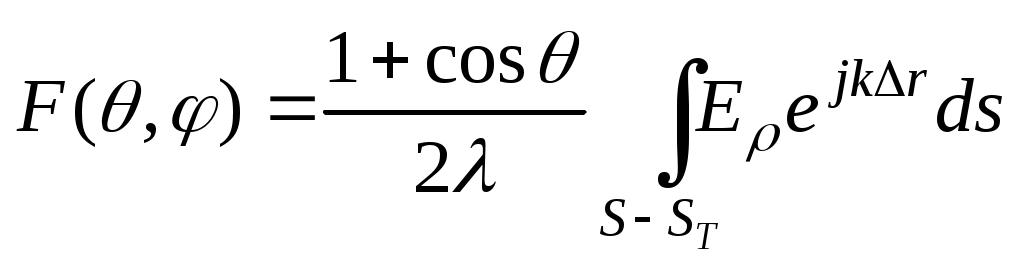 ,
,
где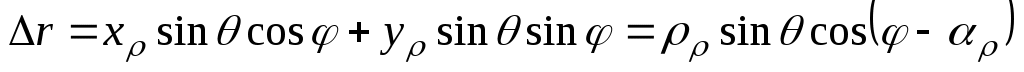 (3.7)
(3.7)
S – площадь поверхности раскрыва; ST – площадь проекции на раскрыв затеняющих элементов.
Коэффициент усиления антенны с учетом апертурного коэффициента использования поверхности γa, обусловленного амплитудной неравномерностью поля в раскрыве, и коэффициента перехвата мощности облучателя зеркалом γn рассчитывается по формуле:
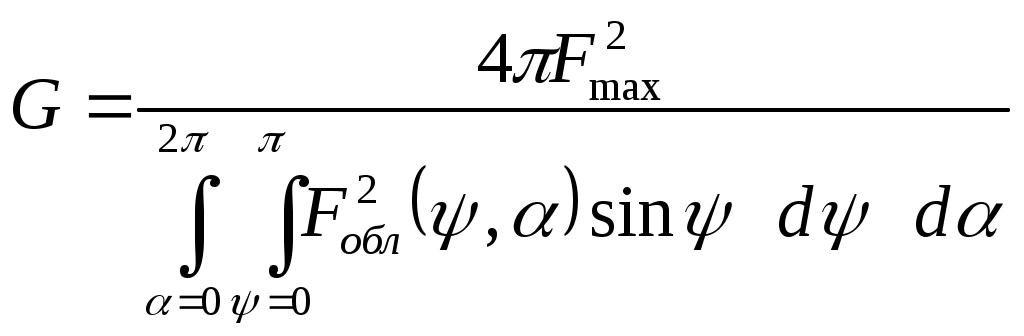 , (3.8)
, (3.8)
где
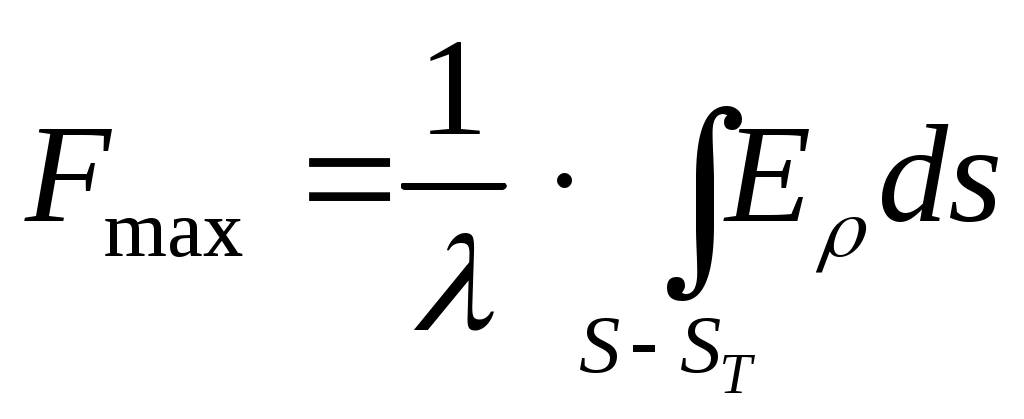
Общая эффективность антенны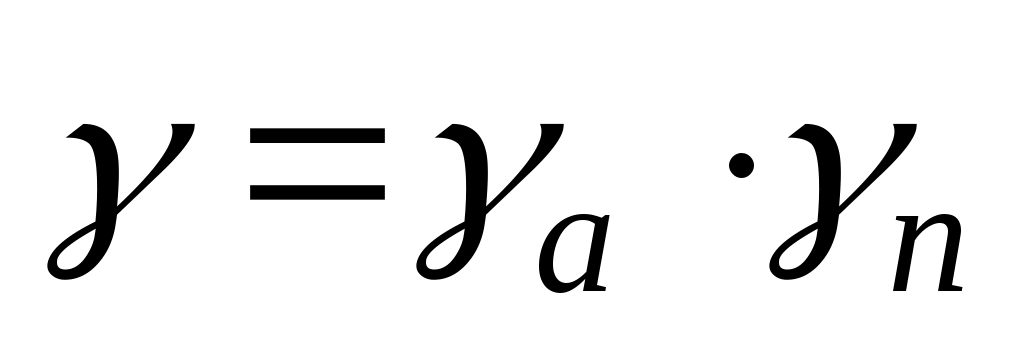 определяется из соотношения:
определяется из соотношения:
 (3.9)
(3.9)
В общем случае расчет диаграммы направленности по формуле (3.7) выполняется численно и только в некоторых случаях, если распределение поля в раскрыве удается аппроксимировать «определенными» функциями, диаграмма направленности может быть выражена через комбинацию известных аналитических функций. Некоторые из таких распределений и соответствующие аппроксимирующие функции и формулы для расчета диаграмм направленностей приведены в таблицах 3.1, 3.2. Подобные законы распределения поля в раскрыве зеркала получаются при использовании наиболее употребительных типов облучателей (рупоров, вибраторов, диэлектрических стержневых спиральных антенн и т.д.) и допускают аналитическое вычисление интеграла (3.7).
Таблица 3.1
Расчетные соотношения для прямоугольного раскрыва
Таблица 3.2
Расчетные соотношения для круглого раскрыва
Рассмотрим два частных случая, широко используемых на практике, амплитудных распределений токов в АР, для которых имеются аналитические формулы расчета ДН:
1. Закон распределения «Косинус на пьедестале»:
ДН в этом случае определяется формулой:
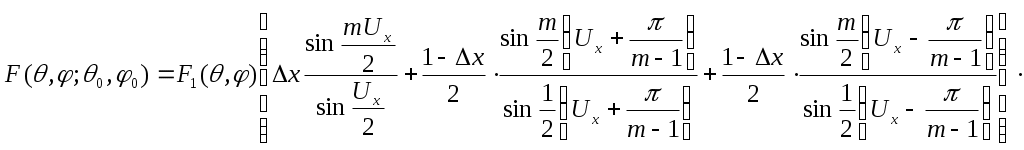
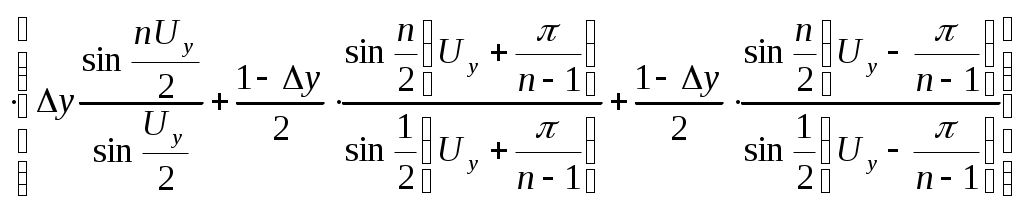 , (2.3)
, (2.3)2. Закон распределения «Косинус квадрат на пьедестале»:
Выражение для ДН
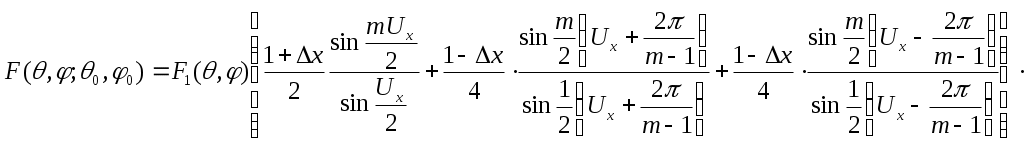
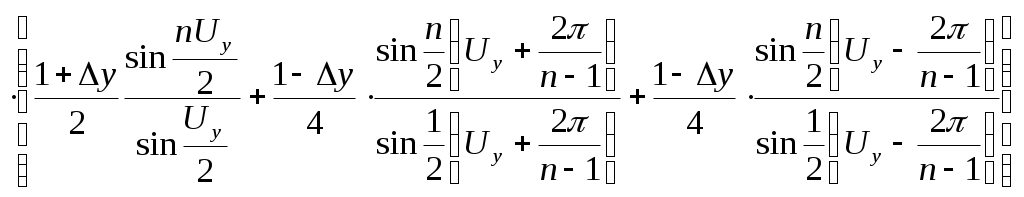 (2.5)
(2.5)Для обоих законов распределения амплитуд
Из формулы (2.2) следует частный случай равноамплитудного распределения (Δx=Δy=1).
Для приближенной численной оценки ширины главного лепестка ДН и УБЛ при таких вариантах возбуждения можно использовать данные табл. 3.1, где приведены соотношения для прямоугольных синфазных и непрерывно возбужденных раскрывов. При этом необходимо помнить, что приведенные расчетные соотношения не учитывают направленные свойства одиночных элементов, возможность отклонения луча от нормали (несинфазное возбуждение элементов) и, что их использование возможно только при достаточно большом числе элементов в строке и столбце с выбором периода решетки в соответствии формулой 6.1.
Используя данные табл. 3.1 видно, что амплитудное распределение токов по элементам влияет на ширину главного лепестка ДН и на УБЛ. Учитывая, что ширина главного лепестка зависит ещё и от размеров решётки, выбор распределения при проектировании антенны производят по УБЛ. В последующем распределение корректируется с учетом направленности одиночных элементов и ростом УБЛ при отклонении луча от нормали.
В двумерной решетке, так же как и в линейной, происходит расширение главного лепестка ДН при отклонении луча от нормали.
Для остронаправленных решёток, у которых
где
КНД ФАР с равномерным по амплитуде распределением определяются следующим выражением:
3. Рефлекторные параболические антенны
Параболические антенны используются для создания остронаправленного излучения за счет преобразования сферического фронта волны облучателя в плоский фронт после отражения ее от зеркала – рефлектора. В трактовке геометрической оптики, справедливой при больших электрических размерах зеркал, это объясняется тем, что для источника, помещенного в точке фокуса параболического отражателя, все отраженные лучи параллельны оси параболоида, а расстояние вдоль лучей от фокуса до плоскости, перпендикулярной оси, одинаковы.
Таким образом, излучение параболической антенны можно свести к излучению плоской синфазной поверхности (раскрыва) больших электрических размеров, которая, как известно, обладает высокой направленностью.
Д
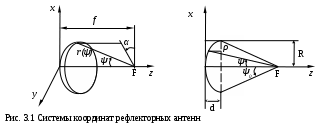 алее будут рассмотрены основные модификации рефлекторных антенн и особенности их расчета.
алее будут рассмотрены основные модификации рефлекторных антенн и особенности их расчета.Чаще всего, рефлектор является симметричной или несимметричной вырезкой из параболоида вращения, который в прямоугольной системе координат (x, y, z) описывается уравнением:
а в сферической (r, Ψ, α), с началом координат в фокусе параболоида:
Радиус раскрыва - R, угол раскрыва - ψ0 и фокусное расстояние - fсвязаны между собой соотношениями:
В большинстве практических случаев 45º<ψ0<90º, так что 0,4<
Из (3.1) легко определить глубину зеркала:
Наиболее просто направленные свойства рефлекторной антенны рассчитываются так называемым апертурным методом, т.е. по полю в ее раскрыве.
При установке в фокусе рефлектора облучателя с диаграммой направленности Fобл(ψ,α) в раскрыве зеркала наводится синфазное поле с амплитудным распределением
При этом координаты точек раскрыва xρ, yρ или ρρ, αρ связаны с углами ψ и α соотношениями, обусловленными геометрией задачи:
По известному полю в раскрыве рассчитывается диаграмма направленности антенны F(θ,φ):
где
S – площадь поверхности раскрыва; ST – площадь проекции на раскрыв затеняющих элементов.
Коэффициент усиления антенны с учетом апертурного коэффициента использования поверхности γa, обусловленного амплитудной неравномерностью поля в раскрыве, и коэффициента перехвата мощности облучателя зеркалом γn рассчитывается по формуле:
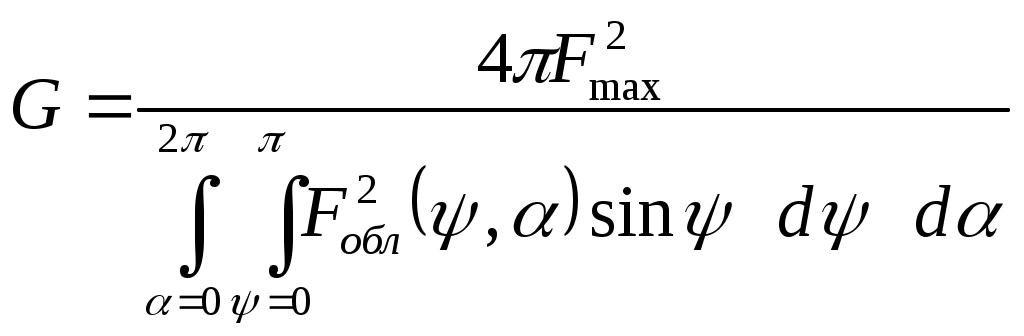 , (3.8)
, (3.8)где
Общая эффективность антенны
В общем случае расчет диаграммы направленности по формуле (3.7) выполняется численно и только в некоторых случаях, если распределение поля в раскрыве удается аппроксимировать «определенными» функциями, диаграмма направленности может быть выражена через комбинацию известных аналитических функций. Некоторые из таких распределений и соответствующие аппроксимирующие функции и формулы для расчета диаграмм направленностей приведены в таблицах 3.1, 3.2. Подобные законы распределения поля в раскрыве зеркала получаются при использовании наиболее употребительных типов облучателей (рупоров, вибраторов, диэлектрических стержневых спиральных антенн и т.д.) и допускают аналитическое вычисление интеграла (3.7).
Таблица 3.1
Расчетные соотношения для прямоугольного раскрыва
| Форма раскрыва | Распределение поля в | Диаграмма направленности | Скачок на краю | Ширина ДН (град.) | Апертур. коэфф. | Уровень боков. | |
| | раскрыве | F(U) | | по нулям | по уровню -3 дБ | использ. раскр. | лепестк. ДБ |
 | 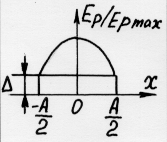 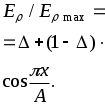 | 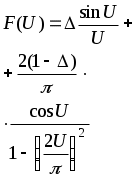 | 0 0.2 0.4 0.6 0.8 1.0 | 171.8 /A 156.3 /A 138.6 /A 130.2 /A 120.3 /A 114.6 /A | 68.8 /A 61.1 /A 58.9 /A 57.4 /A 55.7 /A 50.8 /A | 0.81 0.89 0.94 0.97 0.99 1.0 | -23.0 -21.3 -19.3 -16.5 -14.7 -13.2 |
| | 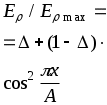 | 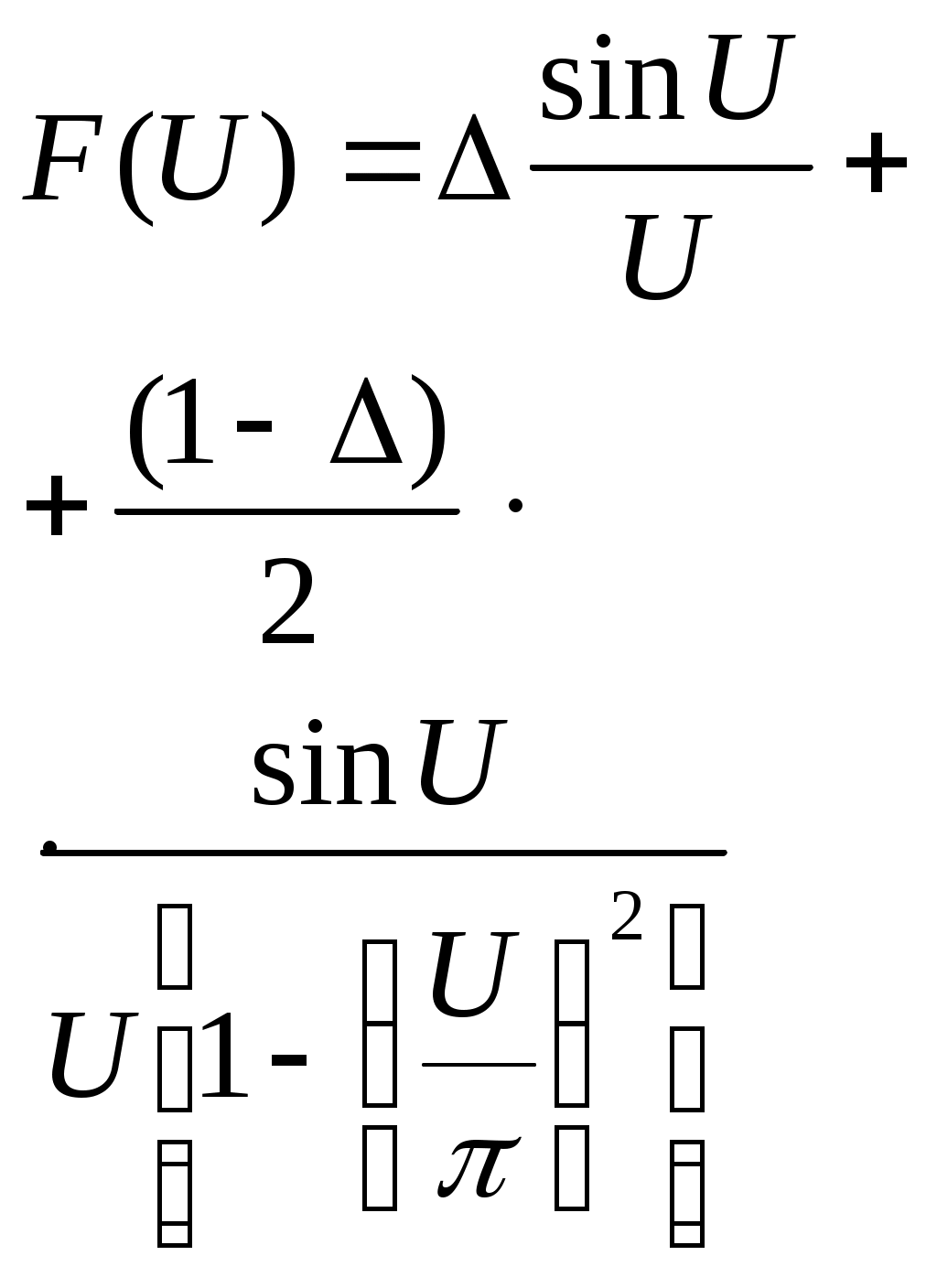 | 0 0.2 0.4 0.6 0.8 |
179.3/A 149.6/A 134.6/A 123.7 /A |
72.2/A 62.7/A 58.3/A 52.0 /A | 0.67 0.82 0.92 0.97 0.99 | -32.0 -30.4 -25.1 -20.0 -15.5 |
Таблица 3.2
Расчетные соотношения для круглого раскрыва
| Форма раскрыва | Распределение поля в | Диаграмма направленности | Скачок на краю | Ширина ДН (град.) | Апертур. коэфф. | Уровень боков. | |
| | раскрыве | F(U) | | по нулям | по уровню -3 дБ | использ. раскр. | лепестк. ДБ |
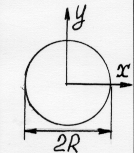 | 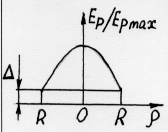 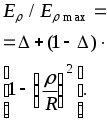 | 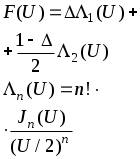 | 0 0.2 0.4 0.6 0.8 1.0 | 186.3 /2R 171.3 /2R 152.9 /2R 145.5 /2R 141.5 /2R 139.6 /2R |
71.0 /2R 66.2 /2R 63.8 /2R 61.2 /2R 58.9 /2R | 0.75 0.87 0.94 0.98 0.99 1.0 | -24.6 -23.5 -21.5 -19.8 -18.6 -17.6 |
| | 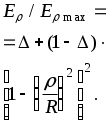 | 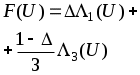 | 0 0.2 0.4 0.6 0.8 |
145.5 /2R |
63.6 /2R | 0.56 0.79 0.91 0.94 0.97 | -30.6 -28.9 -25.4 -23.2 -20.8 |