Федеральное агентство по образованию Российской Федерации

САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИМЕНИ Н.Г.ЧЕРНЫШЕВСКОГО

Кафедра компьютерной алгебры и теории чисел

Основная теорема алгебры

Курсовая работа
студента 1 курса 121 группы механико-математического факультета

Батура Ирина Сергеевна

Научный руководитель Е.В. КОРОБЧЕНКО, ассистент

Зав. кафедрой В.Н.КУЗНЕЦОВ, д.т.н., профессор


САРАТОВ

2009 год
СОДЕРЖАНИЕ
1. Введение

2. Основные определения, используемые в курсовой работе

3. Элементы теории пределов для комплексных чисел

4. Доказательство основной теоремы

5. Список используемой литературы

1. ВВЕДЕНИЕ
Данная работа посвящена Основной теореме Алгебры, изучению существования корней в поле 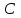. Как предположение эта теорема впервые встречается у немецкого математика Питера Роуте(1617г.). Д’Аламбер первым в 1746г. опубликовал доказательство этой теоремы. Его доказательство основывалось на лемме. Доказательство это было бы совершенно строгим, если бы Д’Аламбер мог доказать, что-то на комплексной плоскости значение модуля многочлена достигает наименьшего значения. Во второй половине 18 века появляются доказательства Эйлера, Лапласа, Лагранжа и других. Во всех этих доказательствах предполагается заранее, что какие-то "идеальные" корни многочлена существуют, а затем доказывается, что, по крайней мере, один из них является комплексным числом. Со времен доказательства теоремы в алгебре было открыто очень много нового, поэтому сегодня "основной" эту теорему назвать уже нельзя: это название теперь является историческим.

Целью моей работы является выявления, что поле 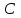комплексных чисел алгебраически замкнуто. Для доказательства Основной теоремы Алгебры я использовала ряд лемм: лемма Даламбера и лемма о достижении точной нижней грани значений.

При написании работы мною была использована следующая литература: Д.К.Фадеев "Лекции по алгебре", Л.Д.Кудрявцев "Курс математического анализа". А.Г.Курош "Курс высшей алгебры".

---

2. Основные определения, используемые в курсовой работе
Множества, удовлетворяющие требованиям:1-операция сложения,2-операция умножения,3-связь операций сложения и умножения, и содержащие хотя бы один элемент, отличный от нуля, называется полями.

Множество комплексных чисел можно определить как множество упорядоченных пар 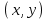действительных чисел, 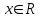, , 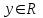в котором введены операции сложения и умножения согласно следующему определению: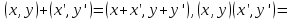

В результате этого определения множество указанных пар превращается в поле, т.е. удовлетворяет условиям 1,2,3. Полученное таким образом поле, называется полем комплексных чисел.

Последовательность комплексных чисел - это функция, определенная на множестве натуральных чисел и имеющая своими значениями комплексные числа.

Последовательность 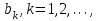называется подпоследовательностью 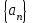, если для любого k существует такое натуральное 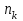, что 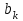= 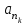, причем 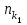Б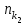 тогда и только тогда, когда .

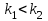Комплексное число – расширение множества вещественных чисел, обычно обозначается . Любое комплексное число может быть представлено как формальная сумма 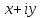, где x и y— вещественные числа, i— мнимая единица, то есть число, удовлетворяющее уравнению .

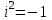Вещественное число (действительное число) – любое положительное число, отрицательное число или нуль.

Функция – 1) Зависимая переменная величина; 2) Соответствие

---

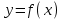между переменными величинами, в силу которого каждому рассматриваемому значению некоторой величины x (аргумента или независимой переменной) соответствует определенное значение величины y (зависимой переменной или функции в значении 1).

Теорема Больцано-Вейерштрасса: из любой ограниченной последовательности можно извлечь сходящуюся подпоследовательность.

Последовательность называется ограниченной на множестве Е, если существует такая постоянная М>0, что для всех 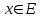и всех 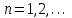выполняется неравенства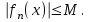

Последовательность сходится к функции f равномерно на множестве Е, если для любого 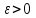существует такой номер 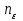, что если 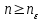, то для всех 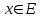выполняется неравенство 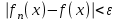. Последовательность называется равномерно сходящейся на множестве Е, если существует функция f, к которой она равномерно сходится на Е.
3. Элементы теории пределов для комплексных чисел
В моей работе полиномы рассматриваются только над полям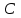и и 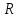как функции от комплексной или вещественной переменной, так что моя работа является скорее главой математического анализа, а не алгебры, хотя теорема о существовании корня у любого отличного от константы полинома с комплексными коэффициентами (т.е. установление алгебраической замкнутости поля 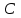) носит название основной теоремы алгебры.

Определение: Пусть задана последовательность комплексных чисел 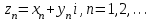. Число 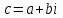называется ее пределом, если для любого действительного числа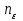 существует такой номер

---

, что при выполняется неравенство 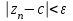. В этом случае пишут lim 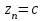, а=lim 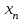, b=lim 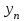. Предельное соотношение lim 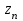=c равносильно соотношению 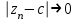, ибо

max
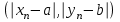
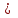
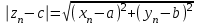
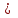
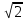
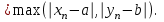
Последовательность 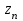такая, что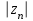 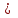R, при некотором R, называется ограниченной.

Для вещественных переменных известная теорема Больцано-Вейерштрасса: из любой ограниченной последовательности можно извлечь сходящуюся подпоследовательность. То же самое верно и для последовательностей, составленных из комплексных чисел.

Действительно, пусть 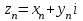ограниченная последовательность, т.е. 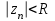, тогда 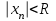, так что 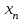есть ограниченная последовательность вещественных чисел. Из нее можно выбрать сходящуюся подпоследовательность 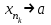. Рассмотрим соответствующую подпоследовательность мнимых частей 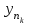. Она ограничена, и из нее можно извлечь сходящуюся подпоследовательность .

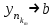Соответствующая подпоследовательность комплексных чисел имеет сходящиеся последовательности вещественных и мнимых частей и, следовательно, сходятся, и ее предел равен .
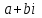4. Доказательство основной теоремы
Прежде чем приступить к формальному доказательству, наметим его идею. Пусть

---

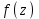-полином, рассматриваемый как функция от комплексной переменной 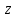.Представим себе "график" функции 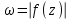, считая , что значения 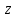изображаются на горизонтальной плоскости, перпендикулярной к плоскости чертежа, а значения 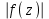откладываются вверх в направлении оси 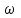. Мы установим, что 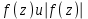являются непрерывными функциями от 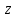на всей плоскости комплексной переменной. 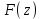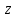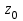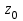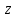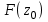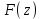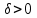Функция от комплексной переменной называется непрерывной в точке , если достаточно близким к значениями соответствует сколь угодно близкие к значения .В более точных терминах - для любого найдется такое , что 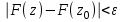, как только .

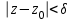Непрерывность 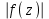дает основания представлять себе график 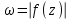в виде непрерывной поверхности, накрывающей плоскость , и местами доходящей до этой плоскости. Собственно говоря, нам и нужно доказать, что существует такое значение

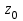, в котором 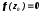, и, тем самым,

---

Смотрите также файлы

• Задание 2 Акробатика.docx

• Отзыв Ваш ответ верный. Вопрос 2.docx

• Лабораторная работа 3 по учебному курсу Физика 3.docx

• Реферат по предмету Нейминг студента 4 курса заочной (с использованием дистанционных образовательных технологий) формы обучения.docx

• Практическая работа 1 фио оу тема Особенности содержания обновленных фгос ооо, фгос соо.docx