ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 28
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
АЛГОРИТМИЗАЦИЯ И ПРОГРАММИРОВАНИЕ
1. Понятие алгоритма
Алгоpитм – это точное и понятное предписание исполнителю совершить последовательность действий, направленных на решение поставленной задачи. Название "алгоритм" произошло от латинской формы имени среднеазиатского математика аль-Хорезми - Algorithmi.
Исполнитель алгоритма - это некоторая абстрактная или реальная (техническая, биологическая или биотехническая) система, способная выполнить действия, предписываемые алгоритмом. Исполнителя характеризуют: среда, элементарные действия, система команд, отказы. Среда (или обстановка) - это "место обитания" исполнителя. Каждый исполнитель может выполнять команды только из некоторого строго заданного списка - системы команд исполнителя. Для каждой команды должны быть заданы условия применимости (в каких состояниях среды может быть выполнена команда) и описаны результаты выполнения команды. После вызова команды исполнитель совершает соответствующее элементарное действие. Отказы исполнителя возникают, если команда вызывается при недопустимом для нее состоянии среды.
В информатике универсальным исполнителем алгоритмов является компьютер.
2. Свойства алгоритмов
Можно выделить следующие основные свойства алгоритмов:
1) Понятность для исполнителя - т.е. исполнитель алгоритма должен знать, как его выполнять.
2) Дискретность (прерывность, раздельность) - т.е. алгоритм должен представлять процесс решения задачи как последовательное выполнение простых или ранее определенных шагов.
3) Определенность - т.е. каждое правило алгоритма должно быть четким, однозначным и не оставлять места для разночтений.
4) Результативность (или конечность). Это свойство состоит в том, что алгоритм должен приводить к решению задачи за конечное число шагов.
5) Массовость - означает, что алгоритм решения задачи pазpабатывается в общем виде, т.е. он должен быть применим для некоторого класса задач, различающихся лишь исходными данными. При этом исходные данные могут выбираться из некоторой области, которая называется областью применимости алгоритма.
3. Формы представления алгоритмов
Наиболее распространенными формами представления алгоритмов
являются: словесная, графическая, псевдокоды и программная.
1) Словесная форма записи представляет собой описание последовательных этапов обработки данных на естественном языке (например, на русском).
Пример. Записать алгоритм нахождения наибольшего общего делителя (НОД) двух натуральных чисел.
Алгоритм: 1) задать два числа; 2) если числа равны, то взять любое из них в качестве ответа и остановиться, в противном случае продолжить выполнение алгоритма; 3) определить большее из чисел; 4) заменить большее из чисел разностью большего и меньшего из чисел; 5) повторить алгоритм с шага 2.
Описанный алгоритм применим к любым натуральным числам и должен приводить к решению поставленной задачи за конечное число шагов.
Словесный способ не имеет широкого распространения, поскольку такие описания:
а) строго не формализуемы;
б) страдают многословностью записей;
в) допускают неоднозначность толкования отдельных предписаний.
2) Графический способ представления алгоритмов является более компактным и наглядным по сравнению со словесным. При графическом исполнении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного из действий. Такое графическое представление называется схемой алгоритма или блок-схемой. В блок-схеме каждому типу действий соответствует геометрическая фигура, называемая блочным символом. Блочные символы соединяются линиями переходов, определяющими очередность выполнения действий.
| Начало - конец | 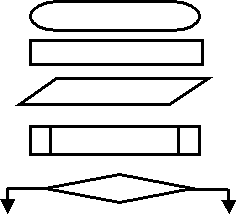 |
| Процесс | |
| Ввод-вывод | |
| Типовой процесс | |
| Решение (условие) |
Подробнее об этом ниже…
3) Псевдокод представляет собой систему обозначений и правил, предназначенную для единообразной записи алгоритмов. Он занимает промежуточное место между естественным и формальным языками.
С одной стороны, он близок к обычному естественному языку, поэтому алгоритмы могут на нем записываться и читаться как обычный текст. С другой стороны, в псевдокоде используются
служебные слова и математическая символика, что приближает запись алгоритма к общепринятой математической записи. Служебные слова выделяются в печатном тексте жирным шрифтом, а в рукописном тексте подчеркиваются для того, чтобы их можно было отличить от остального текста.
Пример. 1) задать два числа x и y; 2) ЕСЛИ x=y, ТО НОД=x и КОНЕЦ; 3) ЕСЛИ x>y, ТО x=x-y, ИНАЧЕ y=y-x; 4) ПЕРЕЙТИ в пункт 2.
4) Программная форма представляет собой тексты программ, написанных на различных языках программирования.
Ниже приведены графические обозначения на блок-схемах.
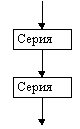 Структура “следование” | 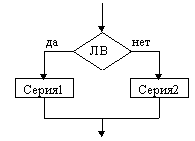 Полная развилка | 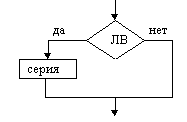 Неполная развилка |
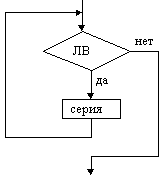 Цикл с предусловие (цикл ПОКА) | 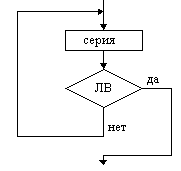 Цикл с постусловием (цикл ДО) | 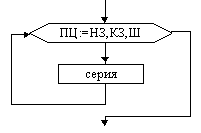 Цикл с параметром |
На схемах СЕРИЯ обозначает один или несколько любых операторов; УСЛОВИЕ есть логическое выражение (ЛВ) (если его значение ИСТИНА, переход происходит по ветви ДА, иначе — по НЕТ). На схеме цикла с параметром использованы обозначения: ПЦ — параметр цикла, НЗ — начальное значение параметра цикла, КЗ — конечное значение параметра цикла, Ш — шаг изменения параметра цикла.
Начало и конец алгоритма на блок-схемах обозначают овалом, вводимые и выводимые переменные записываются в параллелограмме.
Линейные алгоритмы
Простейшие задачи имеют линейный алгоритм решения. Это означает, что он не содержит проверок условий и повторений.
Пример 1. Пешеход шел по пересеченной местности. Его скорость движения по равнине 1 км/ч, в гору —2 км/ч и под гору — 3 км/ч. Время движения соответственно 1, 2 и 3 ч. Какой путь прошел пешеход?
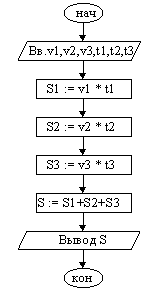 | 1. Ввести v1, v2, v3, t1, t2, t3. 2. S1 := v1 * t1. 3. S2 := v2 * t2. 4. S3 := v3 * t3. 5. S := S1 + S2 + S3. 6. Вывести значение S. 7. Конец. |
Для проверки работоспособности алгоритма необходимо задать значения входных переменных, вычислить конечный результат по алгоритму и сравнить с результатом ручного счета.
Развилка
-
Задачи на ветвление
Разветвляющимся называется такой алгоритм, в котором в зависимости от истинности или ложности заданного условия выбирается один из нескольких возможных вариантов (путей) вычислительного процесса. Каждый такой вариант называется ветвью алгоритма. Возможных вариантов может быть два или три.
Ветвление - такая форма организации действий, при которой в зависимости от выполнения или невыполнения некоторого условия совершается либо одна, либо другая последовательность действий.
Признаком разветвляющегося алгоритма является наличие операций проверки условия.
Условие – это выражение логического типа. Оно может включать в себя константы, имена переменных, арифметические операции, операции отношения, логические операции, скобки. Условие может быть истинным или ложным, то есть принимать одно из двух значений: ИСТИНА или ЛОЖЬ.
Различают два вида условий: простые и составные.
Простым условием называется выражение, составленное из двух арифметических выражений или двух текстовых величин, связанных одним из знаков: <,
Составными условиями называются условия, состоящие из нескольких простых и соединенные знаками логических операций И, ИЛИ, НЕ.
ПРИМЕРЫ составных условий.
(A > 5) И (B < 2)
(X = Y) ИЛИ (50 £ C – 1)
НЕ («собака» = «конура») И («кошка» = D)
Составное условие вида «X И Y» истинно тогда и только тогда, когда истинны оба условия X и Y, в остальных случаях – ложно.
Составное условие вида «X ИЛИ Y» истинно тогда, когда истинно хотя бы одно условие X или Y.
Условие вида «НЕ X» истинно, если X ложно, и наоборот.
Для обозначения операции проверки условия в блок-схеме алгоритма используется блок, изображаемый ромбом, внутри которого указывается проверяемое условие. Этот блок имеет один вход и два или три выхода.
Если выходов два, то они обозначаются ДА и НЕТ. Если условие истинно, то вычислительный процесс «идет» по ветви ДА; если ложно – по ветви НЕТ.
Если выходов три (это чаще всего бывает, когда в условии переменная или выражение сравниваются с нулем), то они обозначаются: >0, <0, =0.
При написании разветвляющихся программ используется условный оператор.
Пример 1. Вычислить значение функции
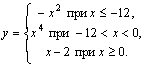
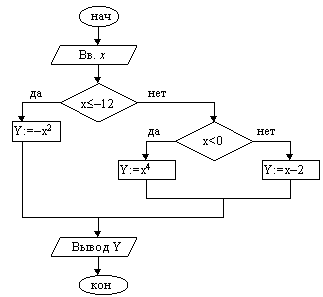 | 1. Ввести x. 2. Если x 3. Если x<0, то y:=x4 4. y := x–2 5. Вывести y 6. Конец |
При тестировании алгоритмов с развилкой необходимо подбирать такие исходные данные, чтобы можно было проверить все ветви. В приведенном выше примере должно быть по крайней мере три тестовых набора.
Циклы
Циклическим называют алгоритм, в котором получение результата обеспечивается многократным выполнением одних и тех же операций. Иными словами, циклическим называют алгоритм, в котором определенная последовательность действий повторяется либо заданное количество раз, либо до тех пор, пока не выполнится некоторое условие. Повторяющаяся последовательность действий называется телом цикла.
Цикл - такая форма организации действий, при которой одна и та же последовательность действий (тело цикла) совершается несколько раз (или ни разу) до тех пор, пока выполняется некоторое условие.
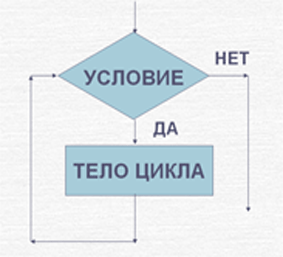
Цикл с предусловием (цикл-пока)
Выполнение начинается с проверки условия, поэтому этот цикл и называется циклом с предусловием. Переход к выполнению серии действий (телу цикла) осуществляется тогда, когда условие истинно, в противном случае происходит выход из цикла. Условие в данном случае называется условием продолжения цикла. Возможен такой вариант, что тело цикла не выполнится ни разу. Для того, чтобы цикл не повторялся бесконечное число раз, в теле цикла необходимо изменять значение параметра цикла так, чтобы за конечное количество «шагов» условие стало ложным.
Блок-схема цикла с предусловием