Файл: 1. Тип 20 26578 Из пункта a в пункт b одновременно выехали два автомобиля.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 147
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1. Тип 20 № 26578
Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути — со скоростью, на 16 км/ч большей скорости первого, в результате чего прибыл в пункт B одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.
Решение. Пусть υ км/ч — скорость первого автомобиля, тогда скорость второго автомобиля на второй половине пути равна
км/ч. Примем расстояние между пунктами за Автомобили были в пути одно и то же время, отсюда имеем:
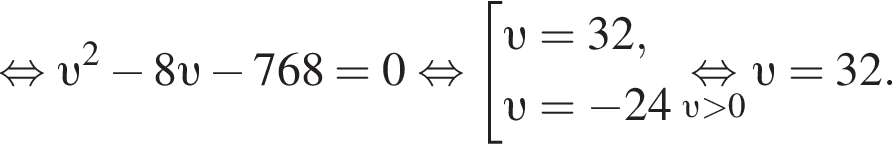
Таким образом, скорость первого автомобиля была равна 32 км/ч.
Ответ: 32.
2. Тип 20 № 26579
Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 13 км/ч, а вторую половину пути — со скоростью 78 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 48 км/ч. Ответ дайте в км/ч.
Решение. Пусть υ км/ч — скорость первого автомобиля, тогда скорость второго автомобиля на первой половине пути равна
км/ч. Примем расстояние между пунктами за 2. Автомобили были в пути одно и то же время, отсюда имеем:
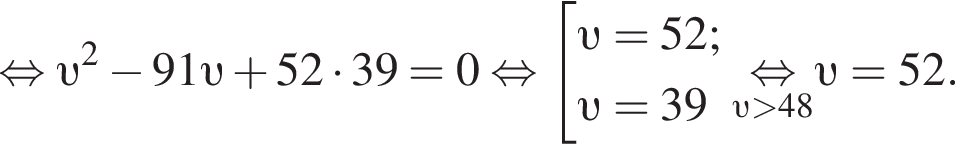
Таким образом, скорость первого автомобиля была равна 52 км/ч.
Ответ: 52.
3. Тип 20 № 26580
Из пункта A в пункт B, расстояние между которыми 75 км, одновременно выехали автомобилист и велосипедист. Известно, что за час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт B на 6 часов позже автомобилиста. Ответ дайте в км/ч.
Решение. Пусть км/ч — скорость велосипедиста, тогда скорость автомобилиста равна
км/ч. Велосипедист был в пути на 6 часов больше, отсюда имеем:
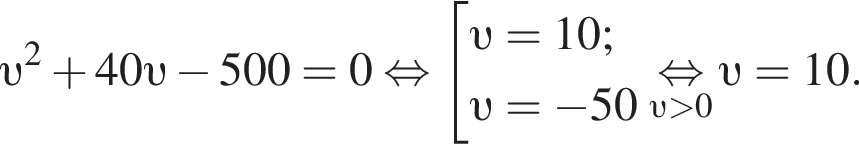
Таким образом, скорость велосипедиста была равна 10 км/ч.
Ответ: 10.
4. Тип 20 № 26581
Велосипедист выехал с постоянной скоростью из города A в город B, расстояние между которыми равно 70 км. На следующий день он отправился обратно в A со скоростью на 3 км/ч больше прежней. По дороге он сделал остановку на 3 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость велосипедиста на пути из B в A. Ответ дайте в км/ч.
Решение. Пусть км/ч — скорость велосипедиста на пути из B в A, тогда скорость велосипедиста на пути из A в B равна
км/ч. Сделав на обратном пути остановку на 3 часа, велосипедист затратил на обратный путь столько же времени, сколько на путь из A в B, отсюда имеем:
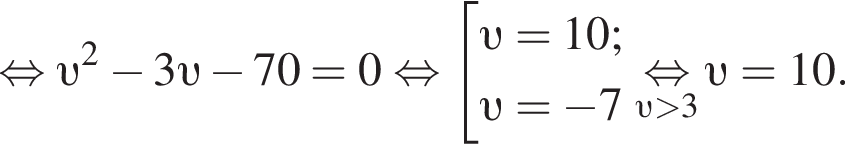
Таким образом, скорость велосипедиста была равна 10 км/ч.
Ответ: 10.
5. Тип 20 № 26582
Велосипедист выехал с постоянной скоростью из города A в город B, расстояние между которыми равно 98 км. На следующий день он отправился обратно со скоростью на 7 км/ч больше прежней. По дороге он сделал остановку на 7 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость велосипедиста на пути из A в B. Ответ дайте в км/ч.
Решение. Пусть υ км/ч — скорость велосипедиста на пути из A в B, тогда скорость велосипедиста на пути из B в A −
км/ч. Сделав на обратном пути остановку на 7 часов, велосипедист затратил на обратный путь столько же времени, сколько на путь из A в B, отсюда имеем:
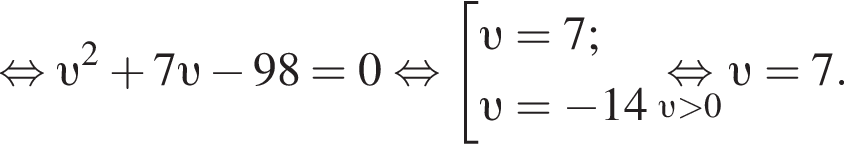
Таким образом, скорость велосипедиста была равно 7 км/ч.
Ответ: 7.
6. Тип 20 № 26583
Два велосипедиста одновременно отправились в 240-километровый пробег. Первый ехал со скоростью, на 1 км/ч большей, чем скорость второго, и прибыл к финишу на 1 час раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым. Ответ дайте в км/ч.
Решение. Пусть км/ч — скорость велосипедиста, пришедшего к финишу первым, тогда скорость второго велосипедиста —
км/ч, 
Первый велосипедист прибыл к финишу на 1 час раньше второго, отсюда имеем:
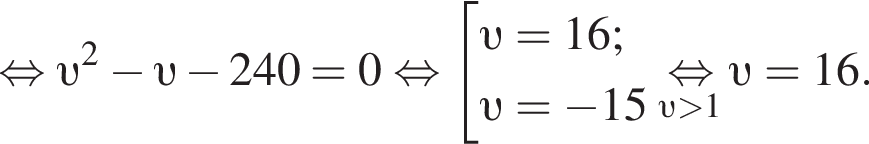
Значит, первым финишировал велосипедист, двигавшийся со скоростью 16 км/ч.
Ответ: 16.
7. Тип 20 № 26584
Два велосипедиста одновременно отправились в 88−километровый пробег. Первый ехал со скоростью, на 3 км/ч большей, чем скорость второго, и прибыл к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
Решение. Пусть км/ч — скорость велосипедиста, пришедшего к финишу вторым, тогда скорость первого велосипедиста равна
км/ч. Первый велосипедист прибыл к финишу на 3 часа раньше второго, отсюда имеем:
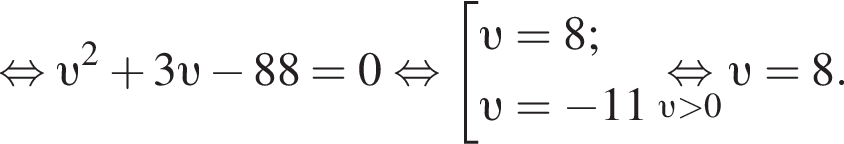
Таким образом, скорость велосипедиста, пришедшего к финишу вторым, равна 8 км/ч.
Ответ: 8.
8. Тип 20 № 99588
Из двух городов, расстояние между которыми равно 560 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 65 км/ч и 75 км/ч?
Решение. Пусть t ч — время движения автомобилей до встречи. Первый автомобиль пройдет расстояние 65t км, а второй − 75t км. Тогда имеем:
Таким образом, автомобили встретятся через 4 часа.
Ответ
: 4.
9. Тип 20 № 99589
Из городов A и B, расстояние между которыми равно 330 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 180 км от города
Найдите скорость автомобиля, выехавшего из города 
Ответ дайте в км/ч.Решение. Автомобиль, выехавший из города A, преодолел расстояние (330 − 180) км = 150 км за 3 часа. Пусть км/ч — скорость данного автомобиля. Таким образом,
км/ч.Ответ: 50.
10. Тип 20 № 99590
Расстояние между городами A и B равно 435 км. Из города A в город B со скоростью 60 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города B выехал со скоростью 65 км/ч второй автомобиль. На каком расстоянии от города A автомобили встретятся? Ответ дайте в километрах.
Решение. Пусть автомобили встретятся на расстоянии S км от города A, тогда второй автомобиль пройдет расстояние
км. Второй автомобиль находился в пути на 1 час меньше первого, отсюда имеем:
Ответ: 240.
11. Тип 20 № 99591
Расстояние между городами A и B равно 470 км. Из города A в город B выехал первый автомобиль, а через 3 часа после этого навстречу ему из города B выехал со скоростью 60 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 350 км от города