Файл: Решение Скорость это есть первая производная от пути, тогда в момент времени, получаем мс.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 06.11.2023

Просмотров: 33

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

1. Зависимость пути от времени при прямолинейном движении точки задана уравнением:

.

Вычислить ее скорость в момент времени .

Решение:

Скорость – это есть первая производная от пути, тогда:



В момент времени , получаем м/с.

2. Составить уравнение касательной к параболе: в точке с абсциссой .

Решение:

Уравнение касательной к графику функции в точке имеет вид:



Находим





Уравнение касательной примет вид:


1. Найти производную функции при данном значении аргумента

а)

б)

в)

Решение:

а)

Находим первую производную



Значение первой производной в точке :



б)


Воспользуемся формулой:

Тогда



Значение первой производной в точке :



в)

Воспользуемся формулой:



Значение первой производной в точке :




2. В прямоугольном параллелепипеде стороны основания равны 7 дм и 24 дм, а высота параллелепипеда равна 8 дм. Определить площадь диагонального сечения.

Решение:

Основание параллелепипеда – прямоугольник со сторонами 7 дм и 24 дм. Тогда его диагональ по теореме Пифагора: дм.

Диагональное сечение – это прямоугольник со сторонами дм и 8 дм (высота).

Тогда площадь диагонального сечения равна:



1. Даны координаты точек А(0;-1;2), В(-1;4;3), С(-2;1;0), D(-1;0;3). Вычислить координаты вектора .

Решение:

Находим





Т.о.



Его длина равна:
2. Выразить через орты вектора , если известно разложение векторов и
:

,

Решение:

Находим



3. Вычислить длину вектора , если известно разложение векторов и :

,

Решение:

Находим



Его длина равна:
2. Найти интегралы:

а)

б)

в)

Решение:

а) Воспользовавшись свойством линейности интегралов, получим


б)

Учитывая, что , то можем записать .

Если положить , то получим табличный интеграл .

Т.е.

в) Воспользовавшись свойством линейности интегралов, получим


3. Скорость точки, движущейся прямолинейно, задана уравнением: . Найти закон движения точки, если за время
с она пройдет путь м.

Решение:

Скорость – это есть первая производная от пути, тогда:

, откуда

Так как за время с она пройдет путь м, то , т.е.

Значит закон движения точки примет вид:

1. В прямом параллелепипеде стороны основания равны 7 см и 17 см; его диагонали образуют с плоскостью основания углы и . Вычислить высоту параллелепипеда.

Решение:


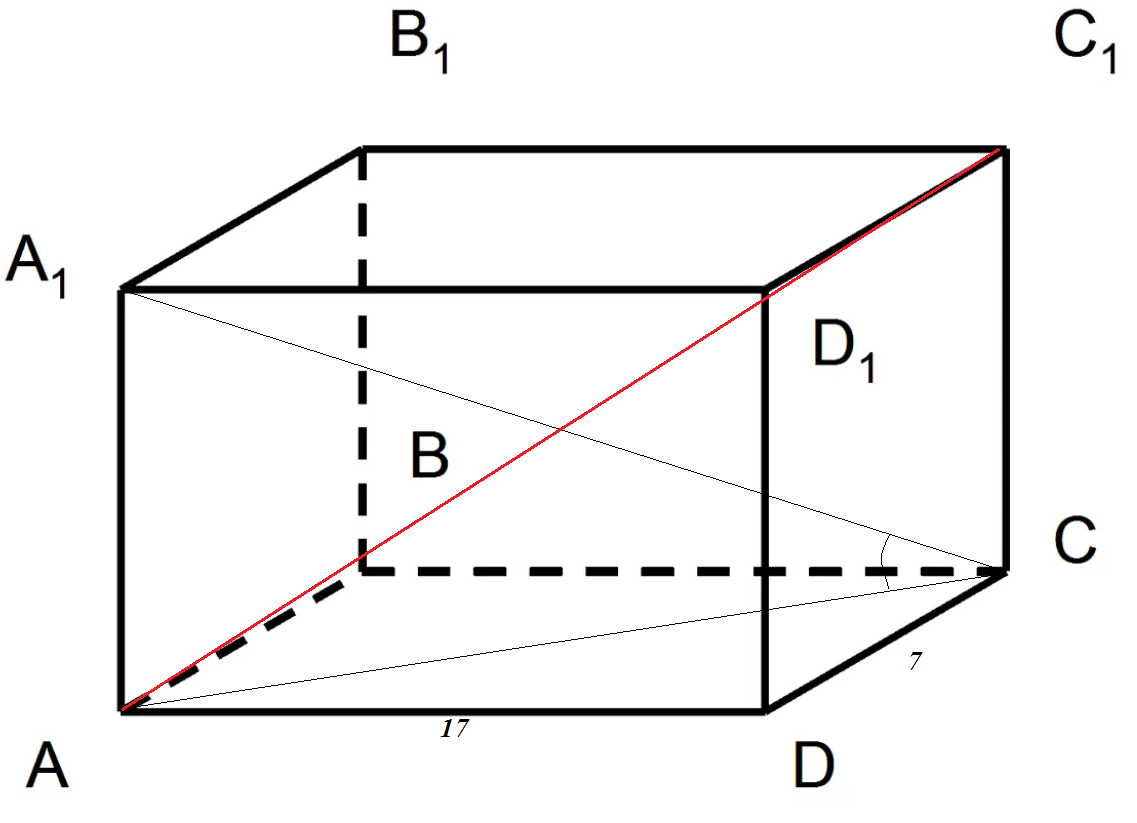
В основании имеем параллелограмм. По теореме косинусов:



По условию , тогда



По условию , тогда



Т.о. получаем уравнение: , т.е. .



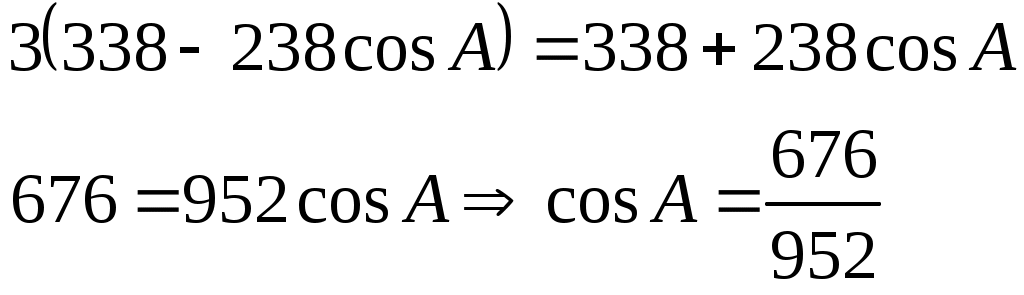
Т.о.

см
1. Вычислить интеграл:

1.

2.

3.

5.

Решение:

Во всех интегралах будем пользоваться формулой Ньютона-Лейбница:

1. Воспользовавшись свойством линейности интегралов, получим



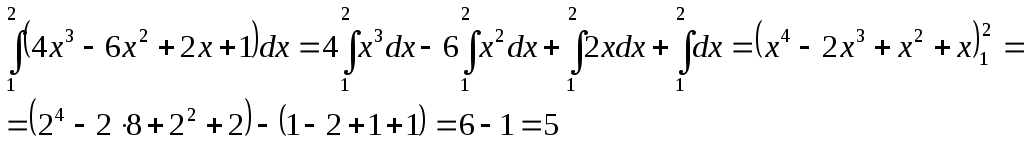
2.



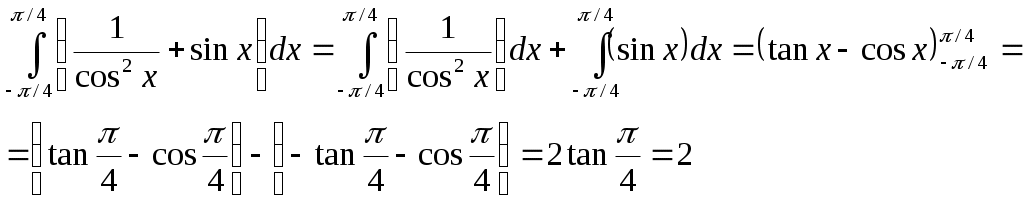
3.

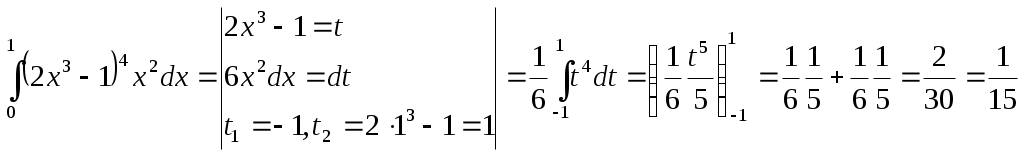
5.



  1. Даны векторы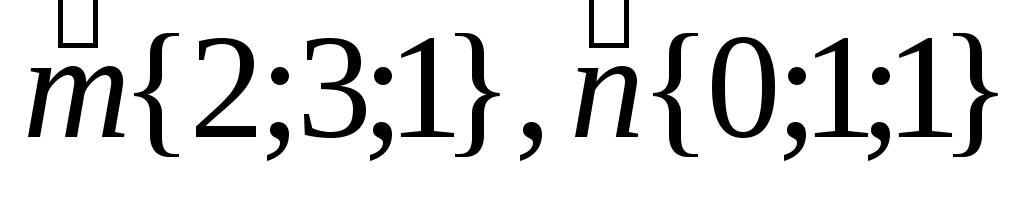 . Вычислить длину вектора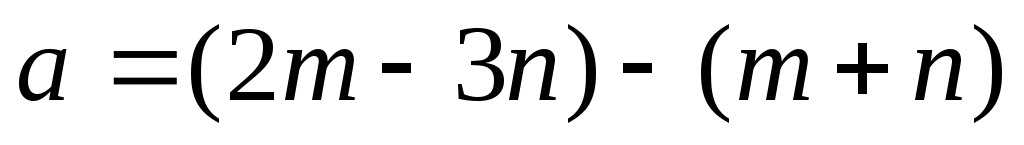

Решение:

Находим





Т.о.

Значит его длина равна:

2. Вычислить скалярное произведение , если ,

Решение:

Для начала найдем

Тогда скалярное произведение будет равно:



3. При каком значении векторы , будут коллинеарны?

Решение:

Условием коллинеарности векторов ,

Смотрите также файлы