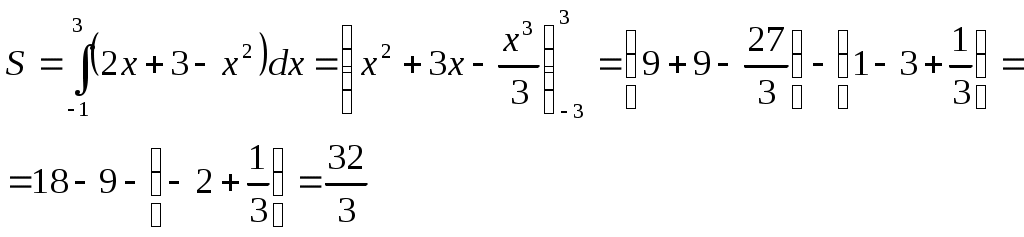Файл: Решение Скорость это есть первая производная от пути, тогда в момент времени, получаем мс.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 34
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
служит условие: 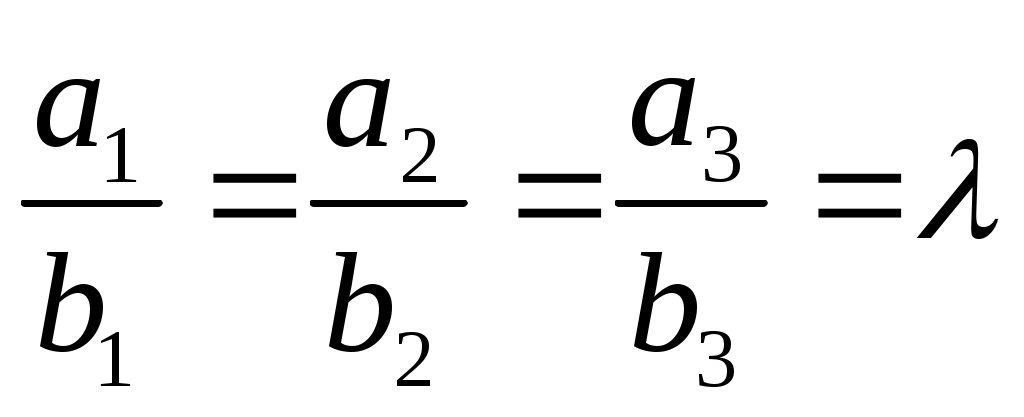
У нас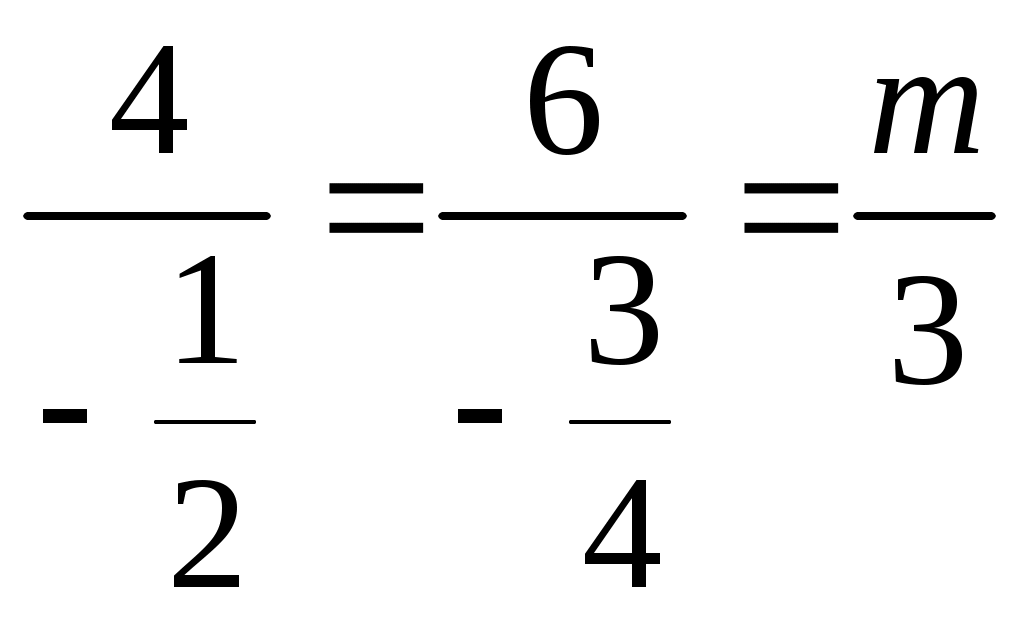 , т.е.
, т.е. 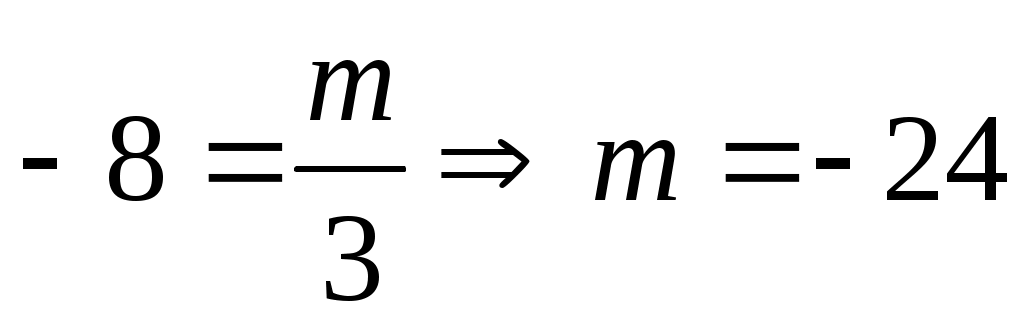
Решение:
Площадь осевого сечения цилиндра – это площадь прямоугольника со сторонами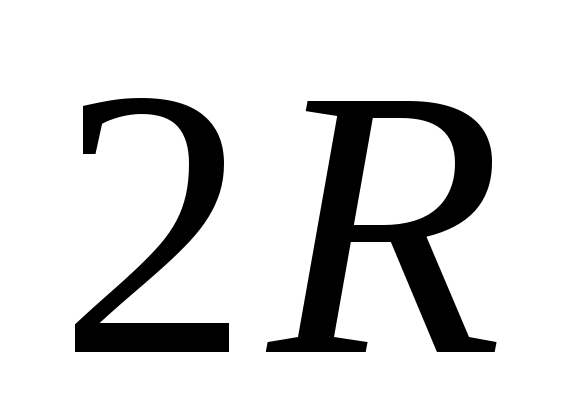 и
и  .
.
Р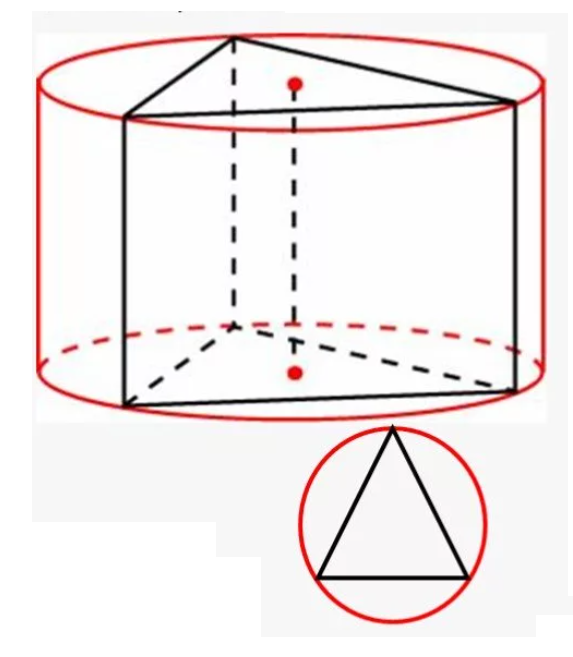 адиус вписанной окружности по формуле:
адиус вписанной окружности по формуле: 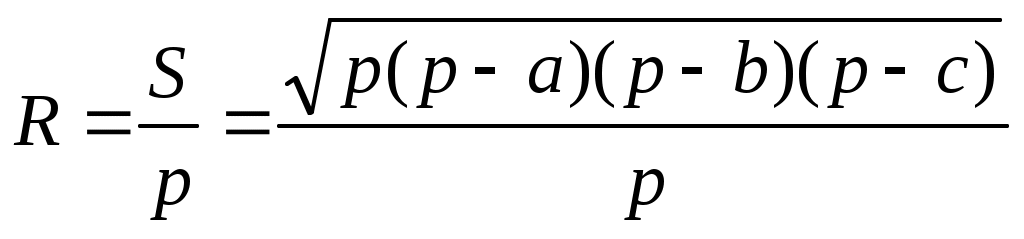 , где
, где 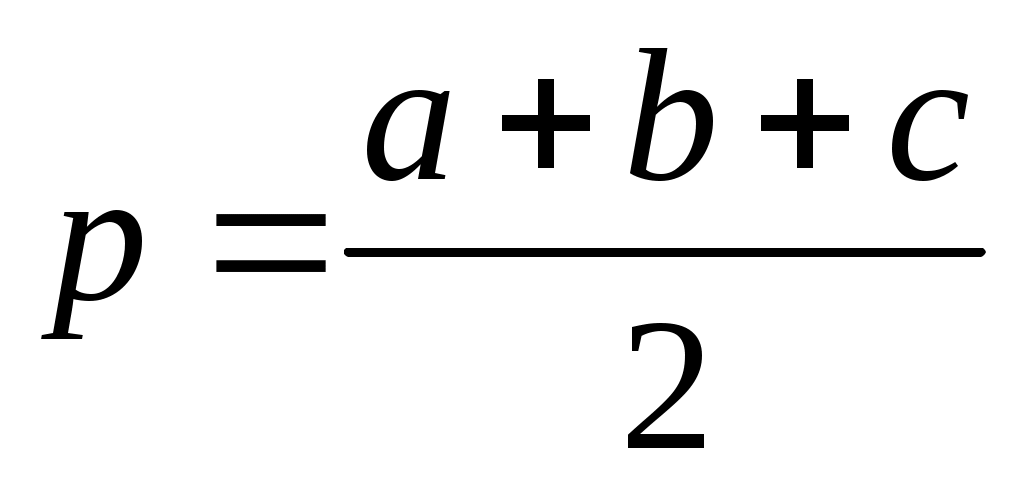 .
.
Находим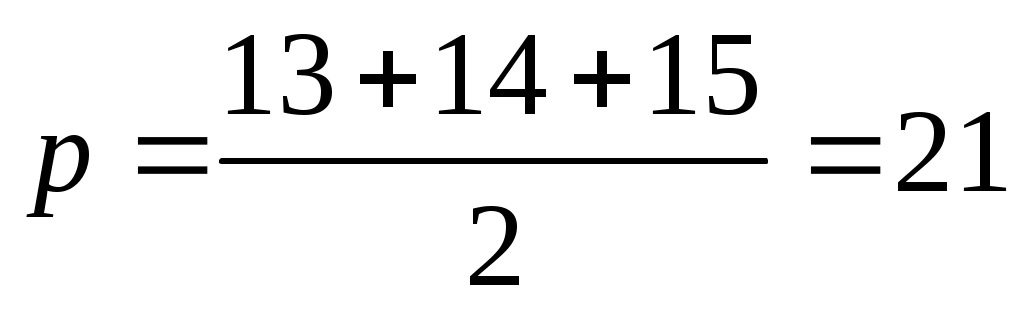 ,
, 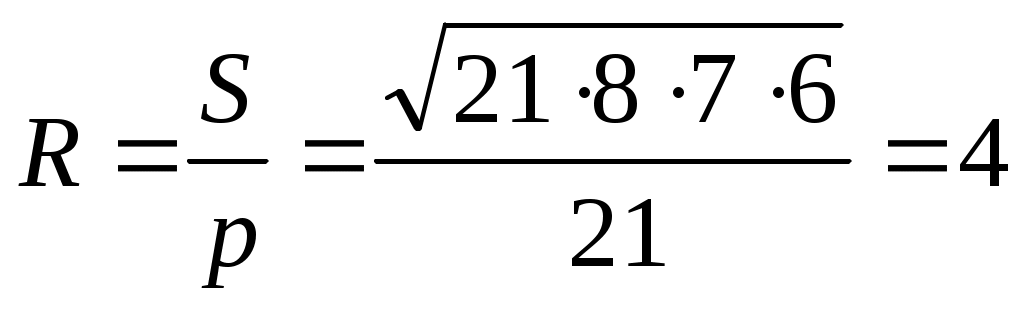
Значит площадь осевого сечения цилиндра равна:
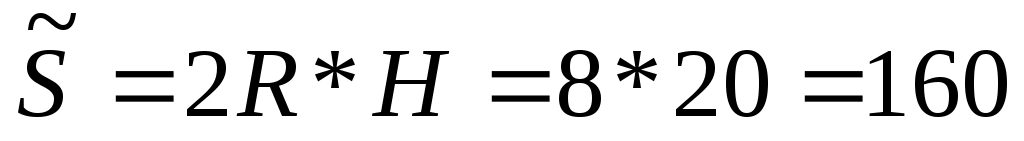 см*см
см*см
Решение:
По теореме Пифагора:
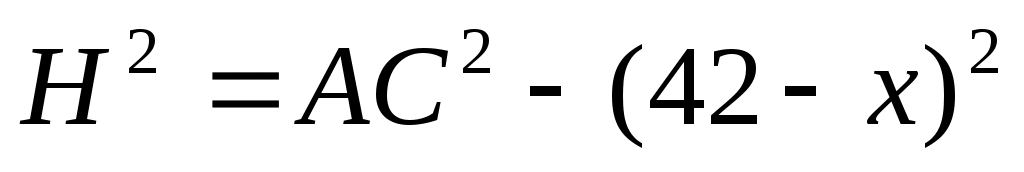 и
и 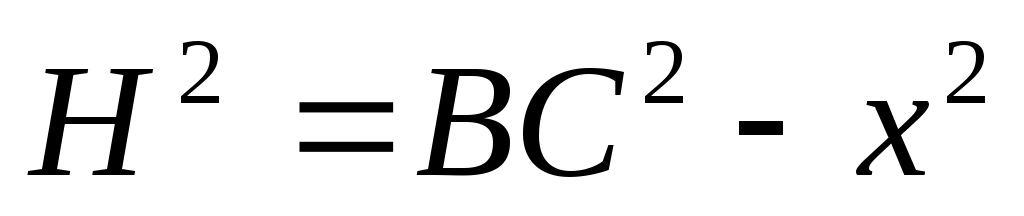 .
.
Отношение дает:
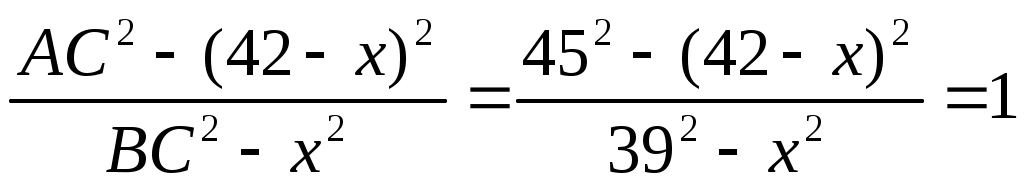
Решаем это уравнение:
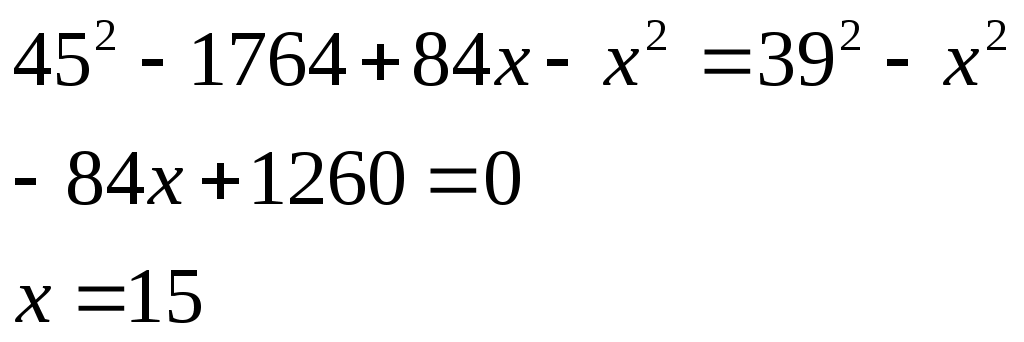
Т.о.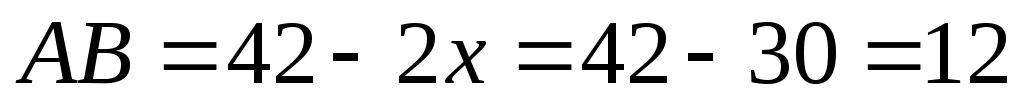 - диаметр меньшего основания, тогда его радиус
- диаметр меньшего основания, тогда его радиус 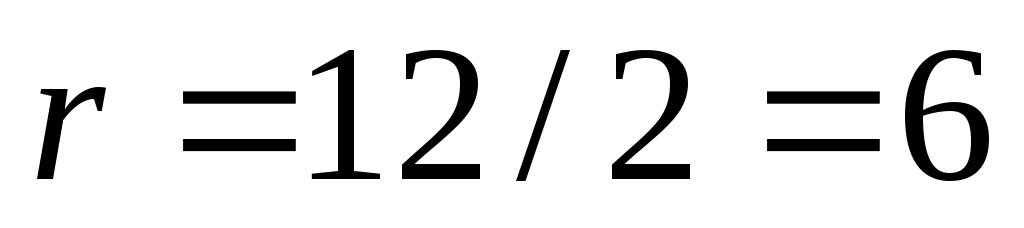 см
см
1. Найти промежутки возрастания и убывания функции: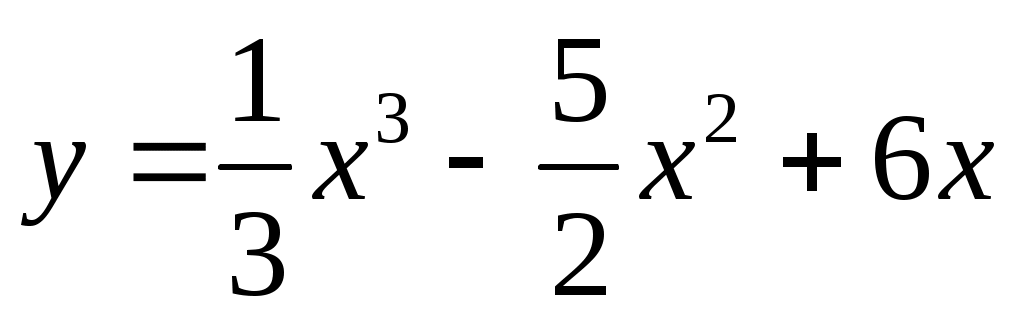
Решение:
Возрастание и убывание функции характеризуется знаком ее производной
характеризуется знаком ее производной  : если в некотором интервале
: если в некотором интервале  , то в этом интервале функция возрастает, а если
, то в этом интервале функция возрастает, а если 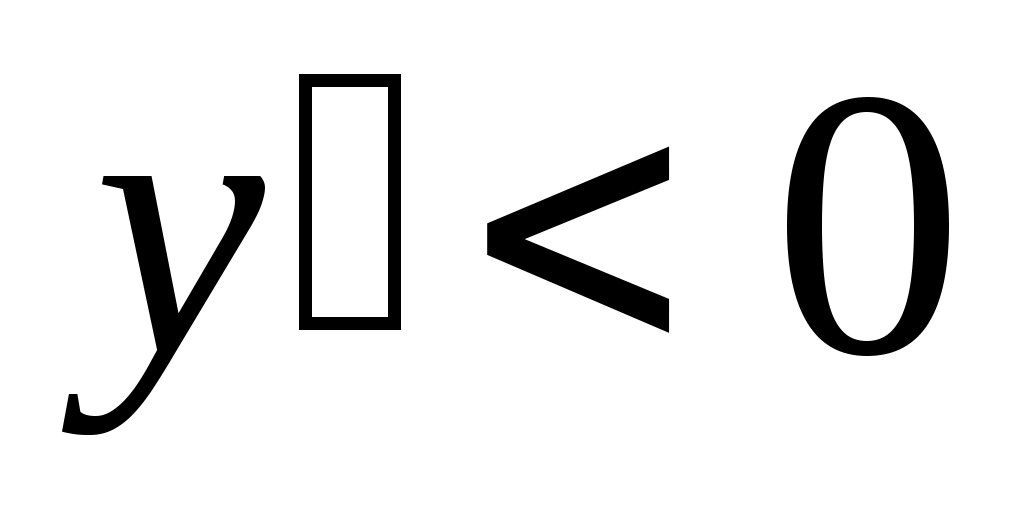 , то функция убывает в этом интервале.
, то функция убывает в этом интервале.
Найдем производную: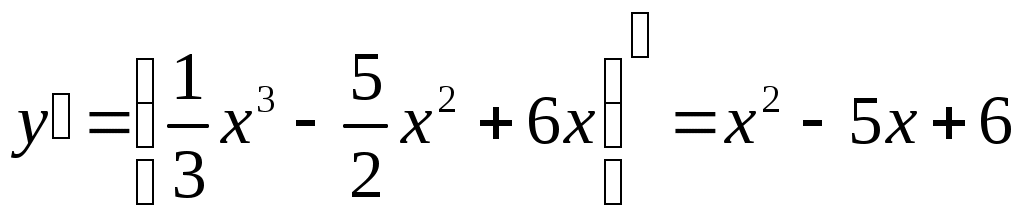 .
.
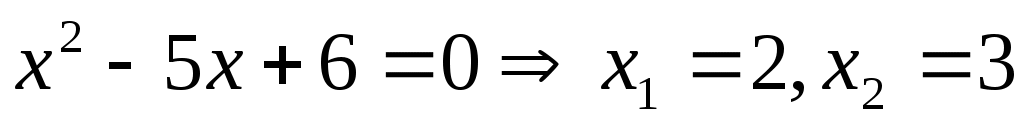
Составим таблицу
Итак, функция убывает на интервале:
убывает на интервале: 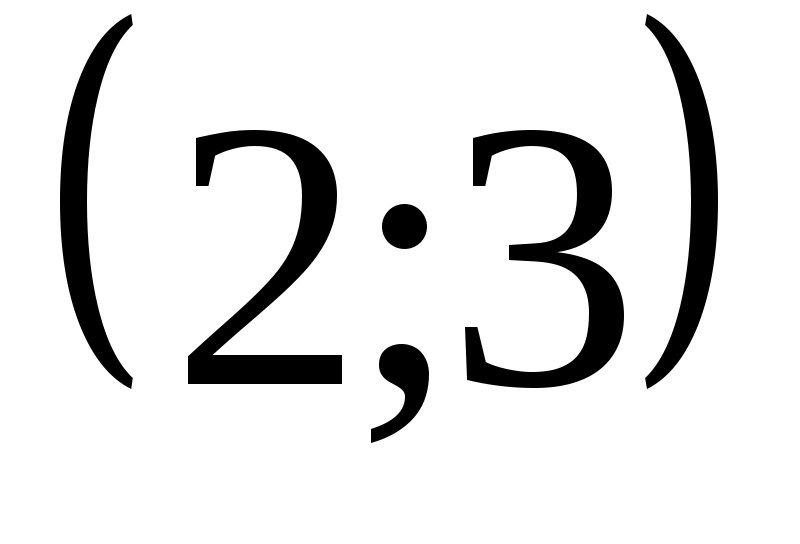 , а возрастает на
, а возрастает на 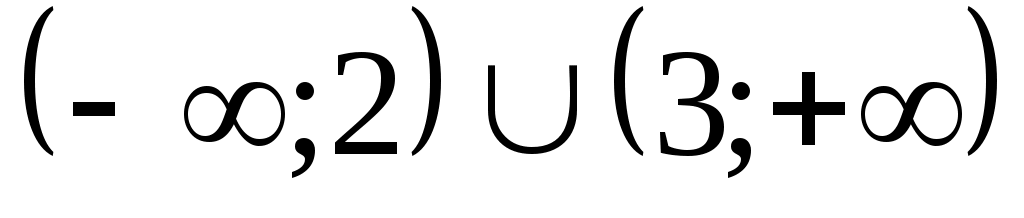
2. Исследовать на экстремум и точки перегиба кривую: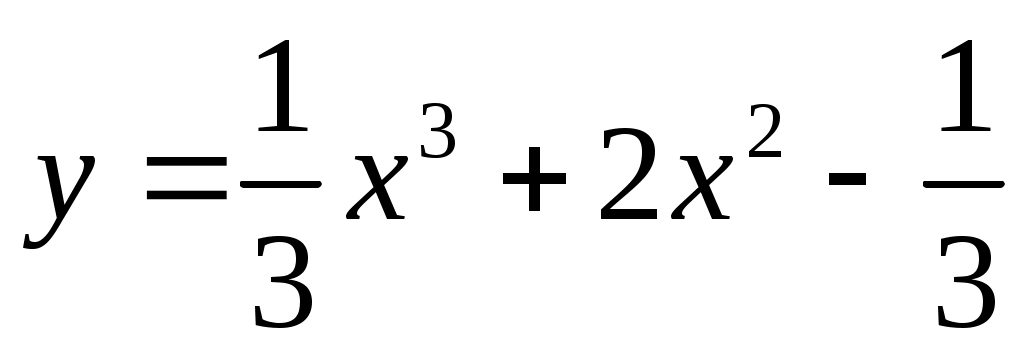 . Построить схематический график этой функции.
. Построить схематический график этой функции.
Решение:
Функция может иметь экстремум только в тех точках, которые принадлежат области определения и в которых ее производная равна нулю или не существует. Если
может иметь экстремум только в тех точках, которые принадлежат области определения и в которых ее производная равна нулю или не существует. Если  меняет знак с “+” на “-” при переходе через исследуемую точку
меняет знак с “+” на “-” при переходе через исследуемую точку
, то эта точка максимума, если меняет знак с “-” на “+” при переходе через исследуемую точку, то эта точка является точкой минимума. Если
меняет знак с “-” на “+” при переходе через исследуемую точку, то эта точка является точкой минимума. Если  не меняет знак при переходе через точку
не меняет знак при переходе через точку  , в этой точке экстремума нет.
, в этой точке экстремума нет.
Найдем первую производную: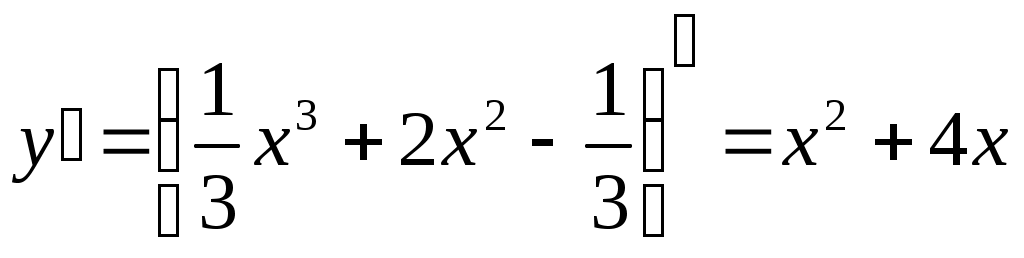
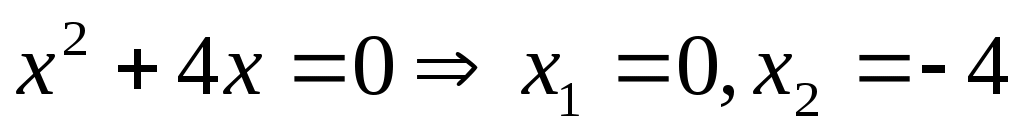
Составим таблицу
Т.о.
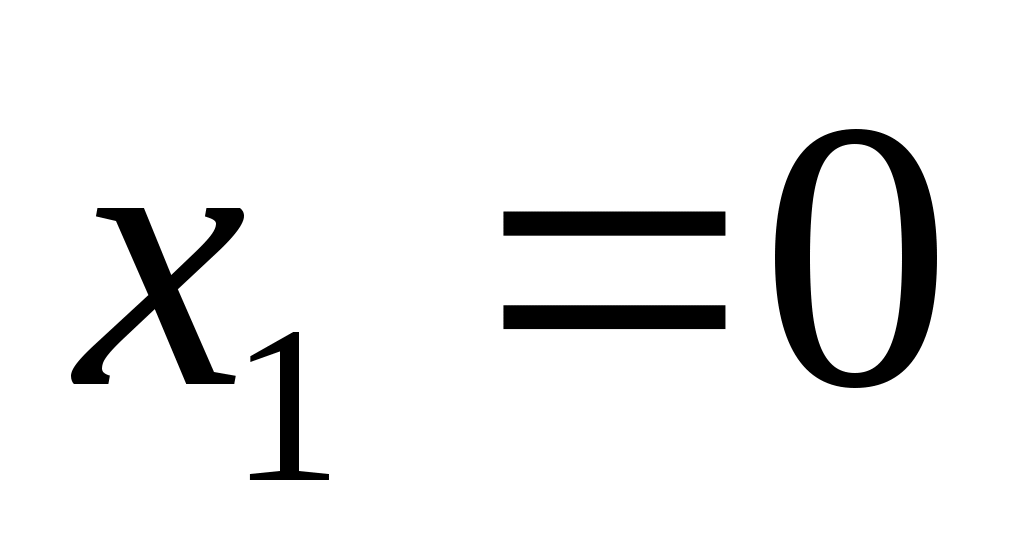 - точка минимума, причем
- точка минимума, причем 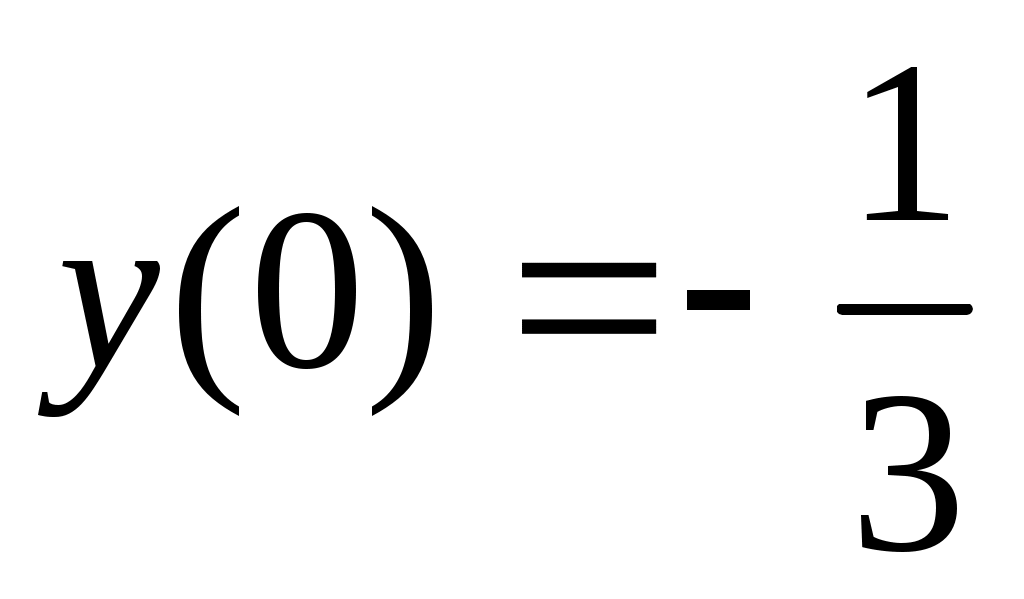
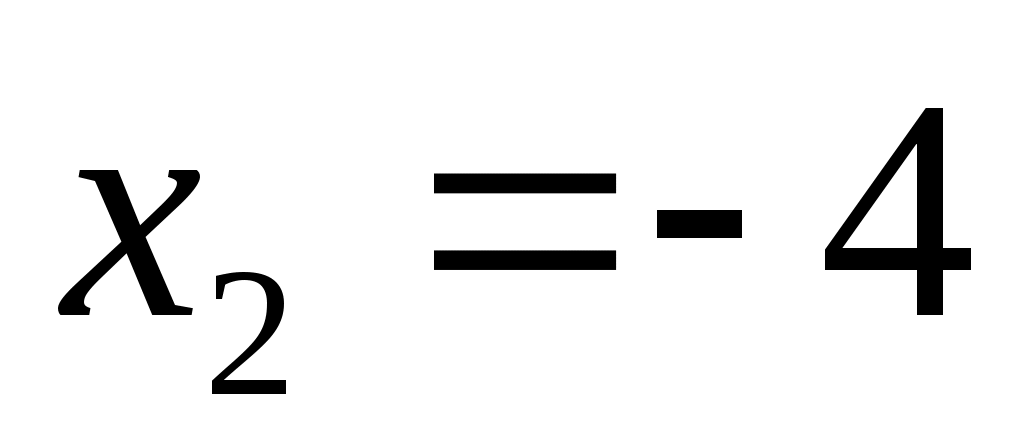 - точка максимума, причем
- точка максимума, причем 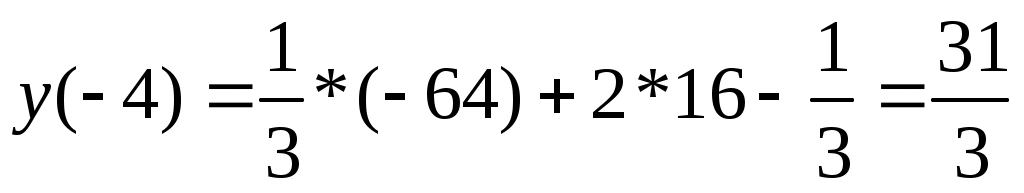
Точки, в которых функция меняет выпуклость на вогнутость или наоборот, называются точками перегиба.
Перегиб возможен в точках, в которых равна нулю или не существует. Если
равна нулю или не существует. Если 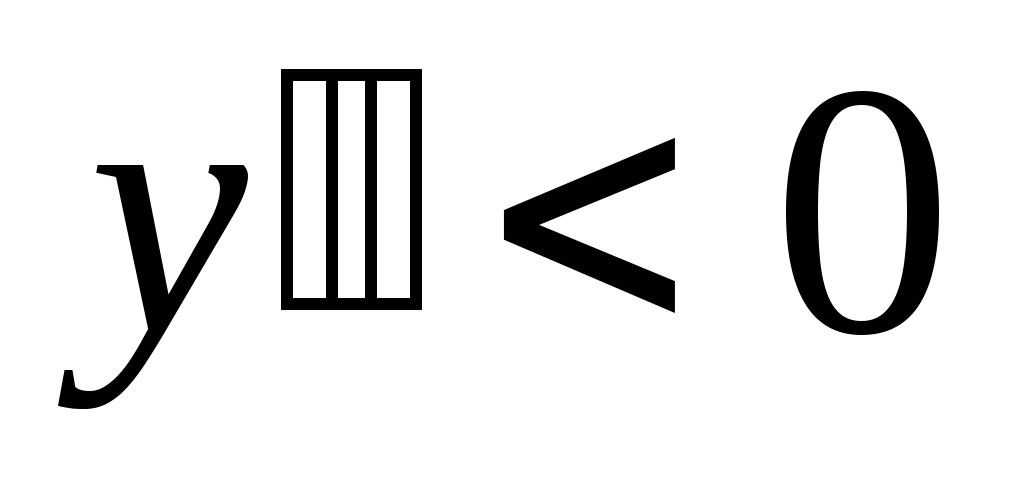 на интервале
на интервале 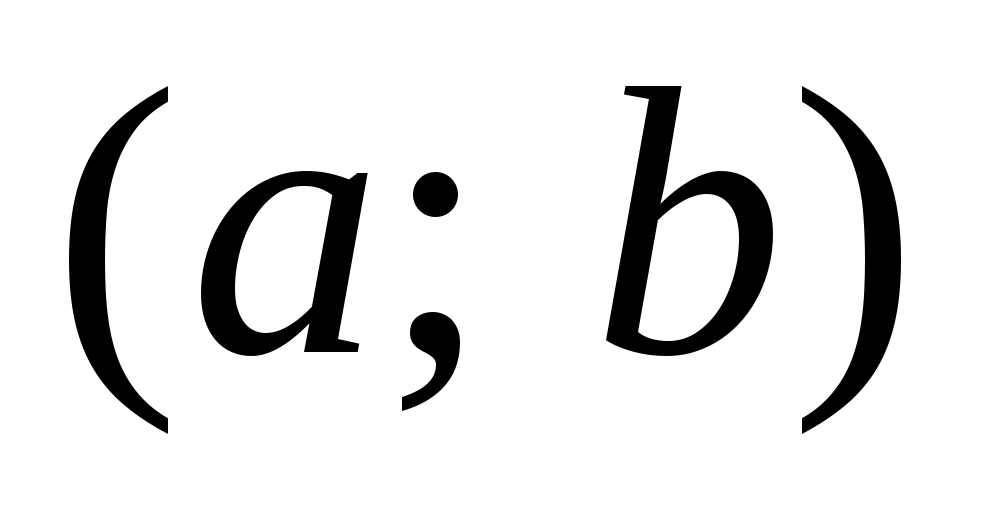
, то график функции является выпуклым на этом интервале, если же
на этом интервале, если же  , то на интервале
, то на интервале  график вогнутый
график вогнутый  .
.
Найдем вторую производную: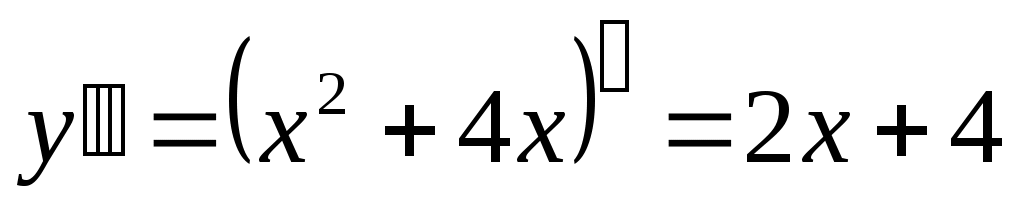
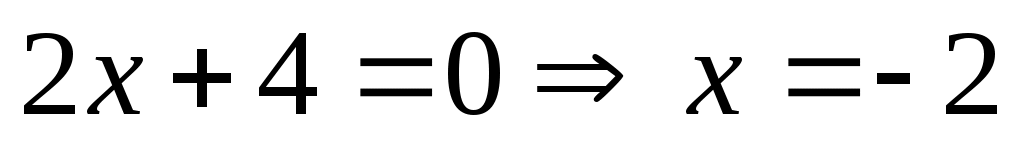
Составим таблицу
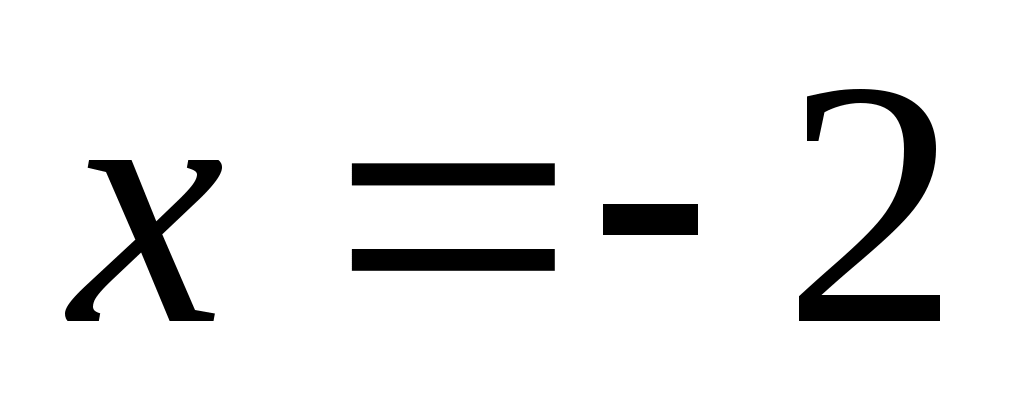 - точка перегиба, причем
- точка перегиба, причем 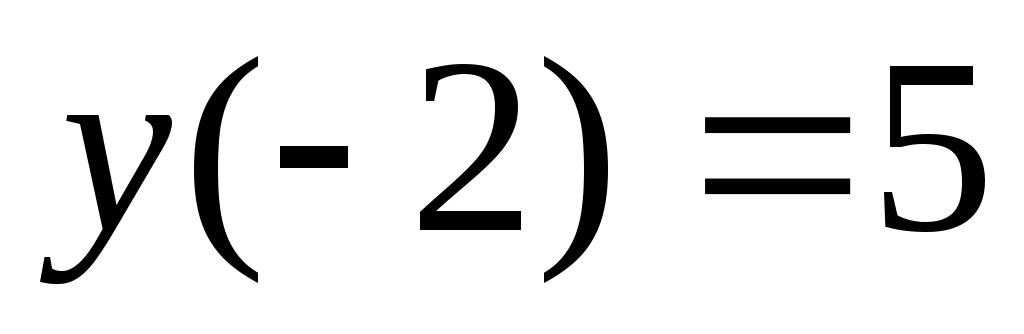
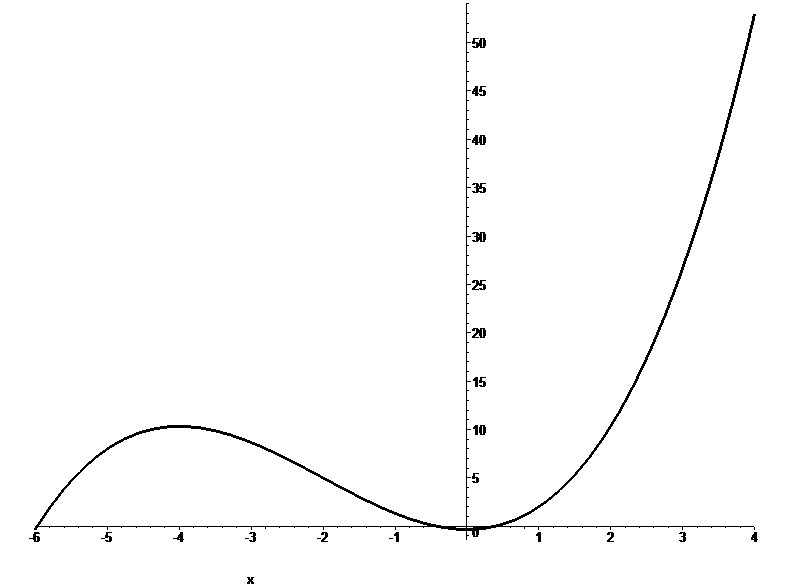
1. вычислить площадь фигуры, ограниченной линиями:
а)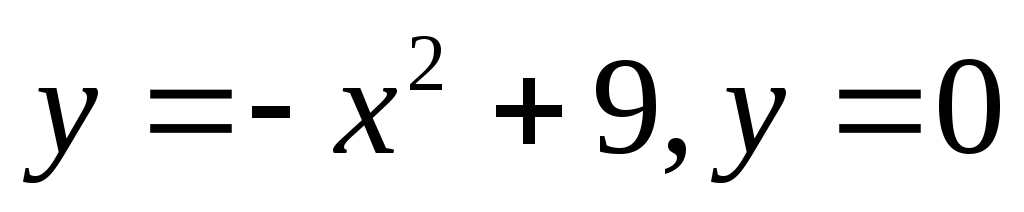
б)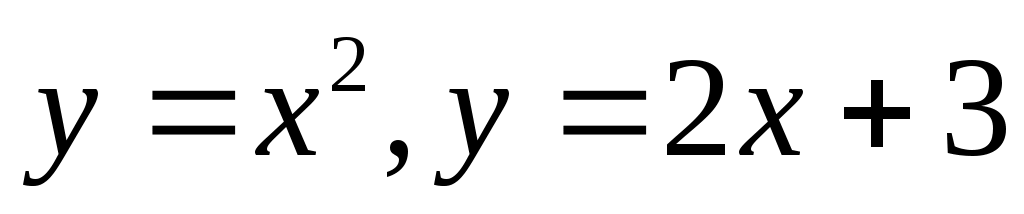
Решение:
а)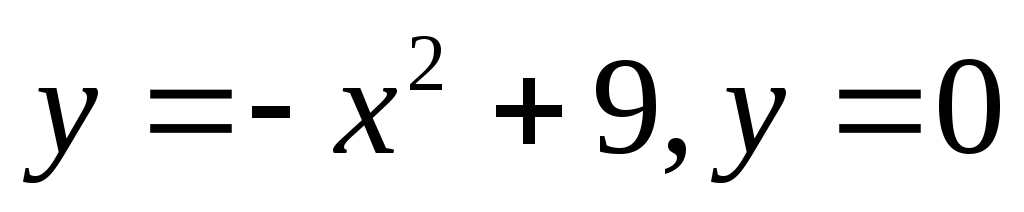
График функции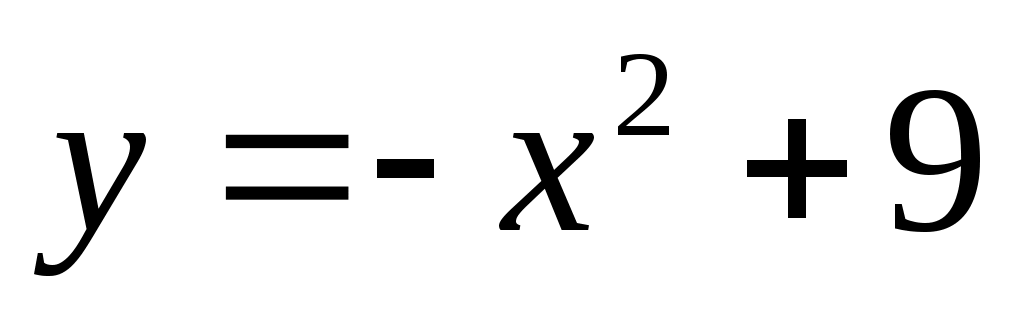 пересекает ось ОХ в точках
пересекает ось ОХ в точках 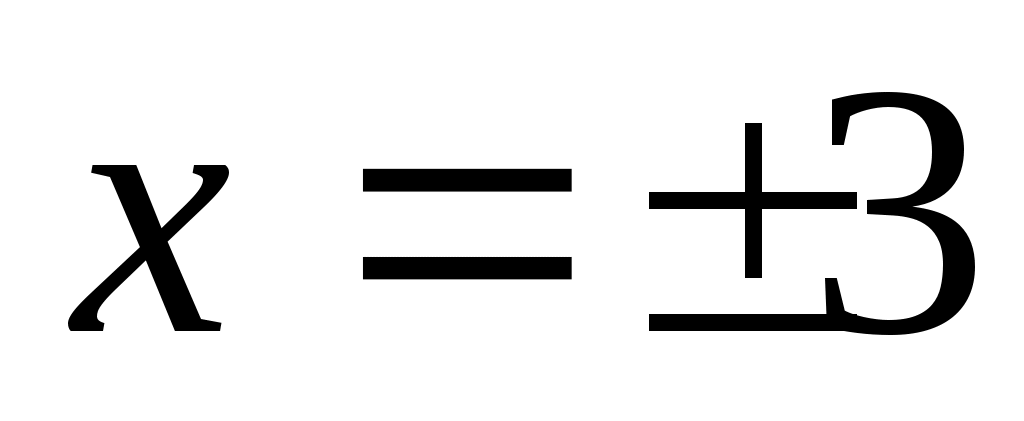 .
.
Площадь фигуры – есть определенный интеграл.
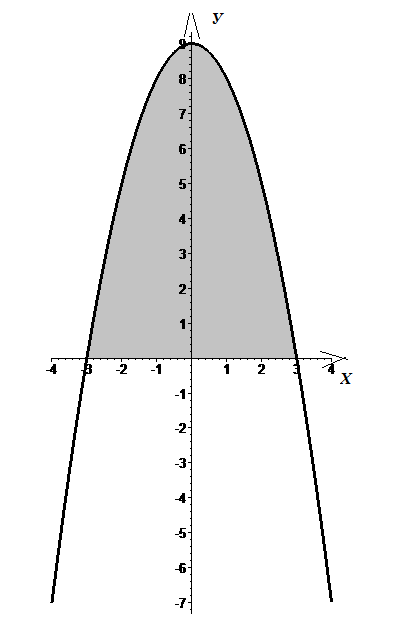
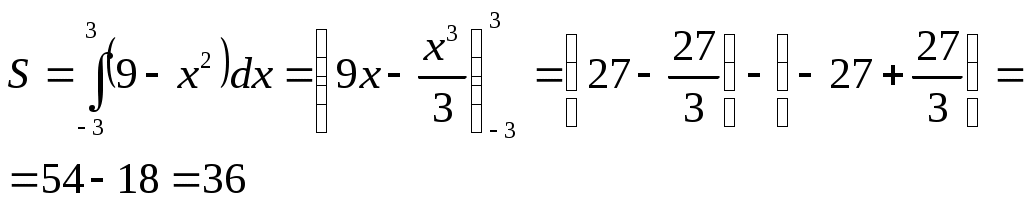
б)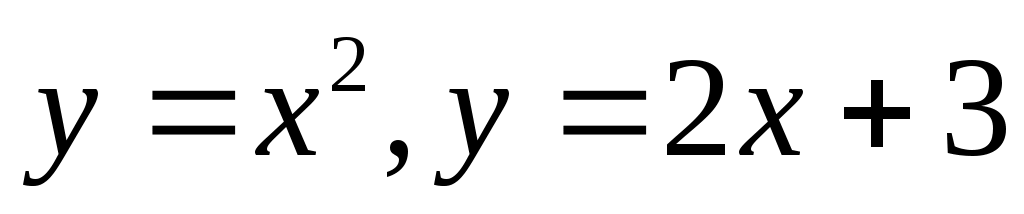
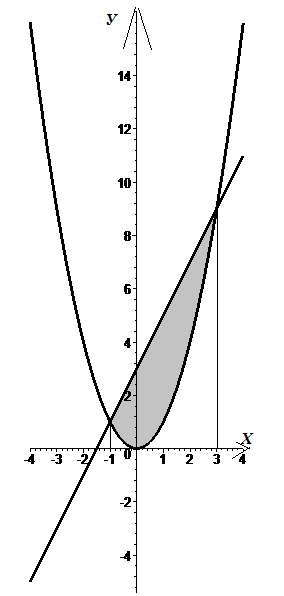
Пересечение графиком функций найдем из уравнения:
найдем из уравнения:
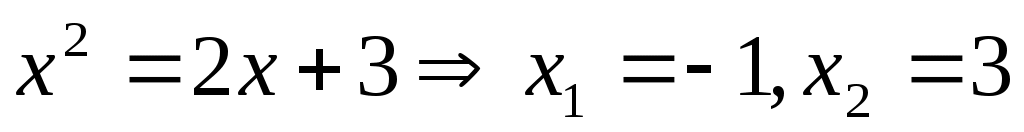
Площадь фигуры – есть определенный интеграл.
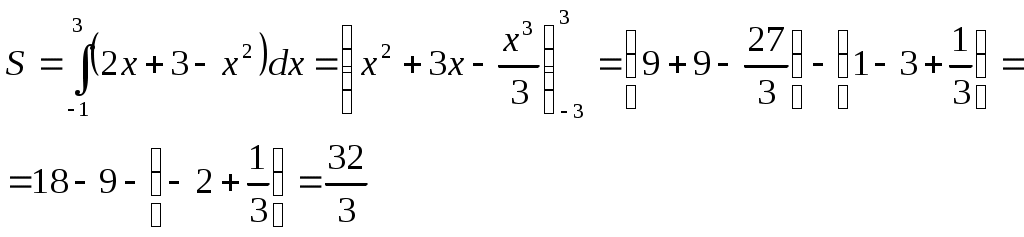
У нас
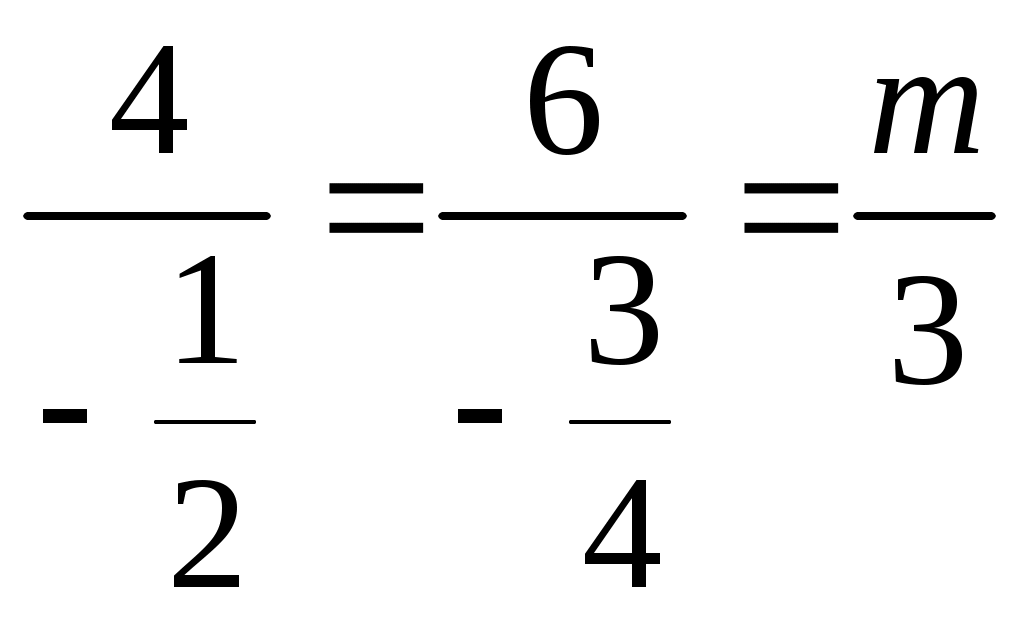 , т.е.
, т.е. -
Цилиндр вписан в прямую треугольную призму, стороны основания которой равны 13 см, 14 см и 15 см, а высота равна 20 см. Требуется вычислить площадь осевого сечения цилиндра.
Решение:
Площадь осевого сечения цилиндра – это площадь прямоугольника со сторонами
Р
 адиус вписанной окружности по формуле:
адиус вписанной окружности по формуле: Находим
Значит площадь осевого сечения цилиндра равна:
-
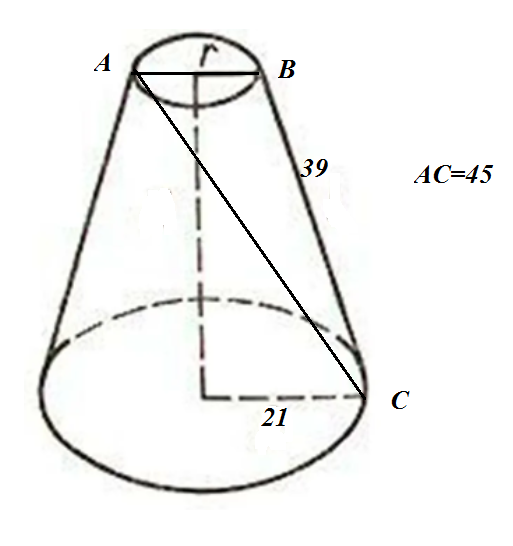
В усеченном конусе радиус большего основания составляет 21 см, образующая 39 см, диагональ осевого сечения 45 см. вычислить радиус меньшего основания.
Решение:
По теореме Пифагора:
Отношение дает:

Решаем это уравнение:
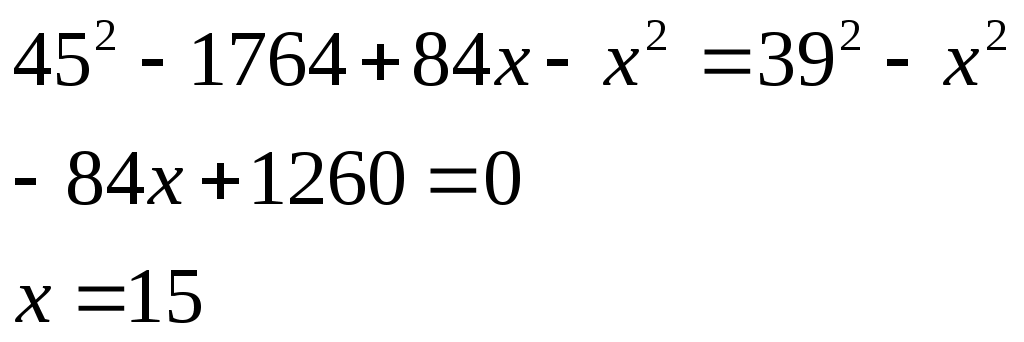
Т.о.
1. Найти промежутки возрастания и убывания функции:
Решение:
Возрастание и убывание функции
Найдем производную:
Составим таблицу
| | | | |
| | + | - | + |
| | возрастает | убывает | возрастает |
Итак, функция
2. Исследовать на экстремум и точки перегиба кривую:
Решение:
Функция
, то эта точка максимума, если
Найдем первую производную:
Составим таблицу
| | | -4 | | 0 | |
| | + | 0 | - | 0 | + |
| | возрастает | точка максимума | убывает | точка минимума | возрастает |
Т.о.
Точки, в которых функция меняет выпуклость на вогнутость или наоборот, называются точками перегиба.
Перегиб возможен в точках, в которых
, то график функции является выпуклым
Найдем вторую производную:
Составим таблицу
| | | -2 | |
| | - | | + |
| | выпуклая | Точка перегиба | вогнутая |

1. вычислить площадь фигуры, ограниченной линиями:
а)
б)
Решение:
а)
График функции
Площадь фигуры – есть определенный интеграл.

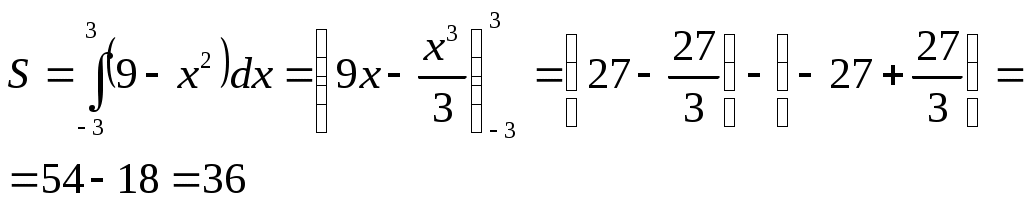
б)

Пересечение графиком функций
Площадь фигуры – есть определенный интеграл.