Файл: 18 Условие жёсткой связи неизменяемые мехе сисмы Конфигурация матго тела Теорема Грасгофа о проекциях скоростей.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 83
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вывод формул для компонент оператора и вектора угловой скорости при плоском движении. Получение соотношений для проекций скоростей двух телесных точек.
Для оператора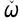 угловой скорости АТТ имеем
угловой скорости АТТ имеем 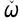 =
=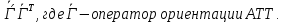
В матричной форме
(*)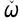 =
= =
=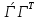
Матрица Г при плоском движении Г=
Вычисляем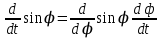 =cos
=cos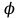
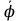
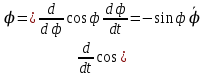 .
.
Поэтому =
=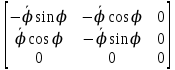
У матрицы 3-я строка нулевая, поэтому в силу (*)
3-я строка нулевая, поэтому в силу (*)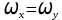 =0.
=0.
Т.к.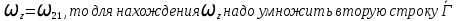 на 1-й столбец
на 1-й столбец 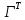 (т.е. на первую строку Г):
(т.е. на первую строку Г):
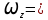 (ϕ ̇cos ϕ)
(ϕ ̇cos ϕ)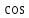 ϕ
ϕ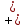 -
-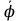 sinϕ
sinϕ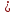 (-sinϕ )
(-sinϕ )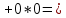
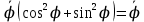
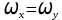 =0,
=0, 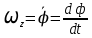
Ед. для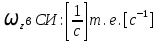
Вывод: угловая скорость АТТ в плоском движении – вектор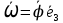 , где
, где 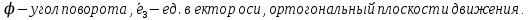
Для оператора угловой скорости: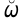 =
=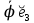 , а в матричной записи
, а в матричной записи 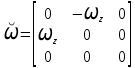 =
=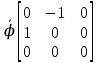
Пусть теперь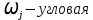 скорость j-ого тела, а телесные точки А* и В* движутся в плоскости движения Оxy. Пусть
скорость j-ого тела, а телесные точки А* и В* движутся в плоскости движения Оxy. Пусть 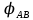 – угол, образуемый направленным отрезком
– угол, образуемый направленным отрезком 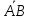 с положительным
с положительным
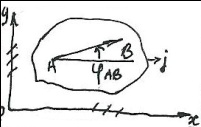
направлением оси Ох.
Т.к. ≡0,
≡0, 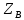 ≡0, то
≡0, то 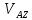 =0 и
=0 и 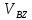 =0
=0
Переход от А к В представим графом (1) А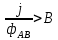
Подставим теперь в ф-лу Эйлера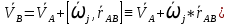
В матричной записи (2)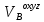 =
=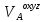 +
+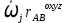
Здесь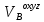 =
=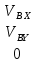 ,
, 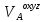 =
=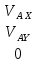 ,
, 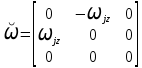 ,
, 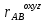 =
=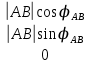
Переходя к компонентной записи из (2) получаем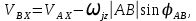
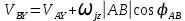 ,
,
Эти формулы соответствуют графу (1).
Аналитический метод решения задач кинематики
Пример составного графа:
А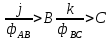
Распишем данный граф:
(1)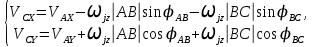
Соотношения (1) верны при следующем основном дополнении – скорости тех точек j-ого и k-ого тел, текущим положение которых служит т. В
Порядок решения типичных задач:
31. Решение задачи о разложении вектора на параллельную и ортогональную составляющие. Вычисление вектора угловой скорости по вектору относительной скорости при плоском движении.
Лемма: формула (*)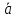 =(
=(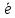 ,
,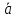 )
)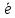 +[
+[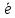 ,[
,[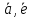 ]] дает разложение вектора
]] дает разложение вектора 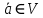 на 2 составляющие:
на 2 составляющие:

параллельную и ортогональную заданному ед. вектору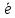
Док-во: проекция вектора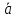 на направлении вектора
на направлении вектора 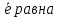 (
(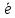 ,
,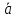 ) так, что
) так, что 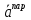 =(
=(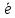 ,
,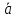 )
) 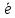
Применяем формулу «БАЦ» минус «ЦАП» для двойного векторного произведения
[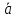 ,[
,[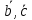 ]]=
]]=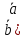 ,
,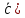 -
-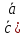 ,
,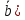 , получаем [
, получаем [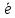 ,[
,[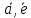 ]]=
]]=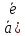 ,
,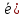 -
-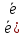 ,
,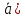 =
=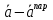 =
=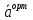
Найдем угловую скорость тела , если известны вектор
, если известны вектор 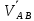 ≡
≡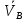 -
-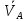
Запишем ф-лу Эйлера в виде (**)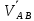 =[
=[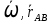 ]
]
Разложим вектор на 2 составляющие: параллельную и ортогональную вектору
на 2 составляющие: параллельную и ортогональную вектору 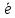 =
=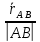
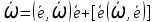 =
=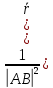 [
[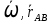 ]] в силу (**):
]] в силу (**):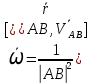 .
.
Замечание: поскольку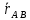 =(
=(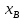 -
-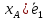 +(
+(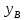 -
-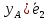 ,
, 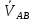 =(
=(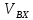 -
-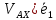 +(
+(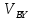 -
-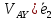 ,
,
то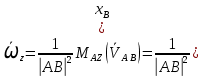 -
-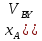 -
-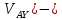 (
(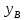 -
-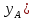 (
(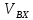 -
-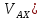 ]
]
Для оператора
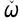 угловой скорости АТТ имеем
угловой скорости АТТ имеем 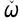 =
=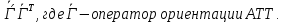
В матричной форме
(*)
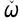 =
= =
=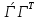
Матрица Г при плоском движении Г=

Вычисляем
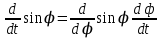 =cos
=cos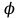
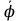
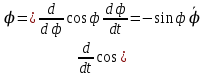 .
.Поэтому
 =
=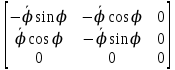
У матрицы
 3-я строка нулевая, поэтому в силу (*)
3-я строка нулевая, поэтому в силу (*)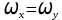 =0.
=0.Т.к.
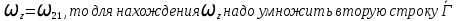 на 1-й столбец
на 1-й столбец 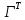 (т.е. на первую строку Г):
(т.е. на первую строку Г):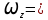 (ϕ ̇cos ϕ)
(ϕ ̇cos ϕ)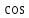 ϕ
ϕ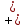 -
-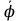 sinϕ
sinϕ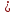 (-sinϕ )
(-sinϕ )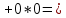
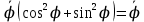
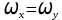 =0,
=0, 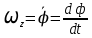
Ед. для
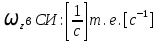
Вывод: угловая скорость АТТ в плоском движении – вектор
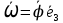 , где
, где 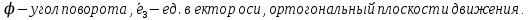
Для оператора угловой скорости:
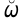 =
=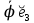 , а в матричной записи
, а в матричной записи 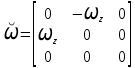 =
=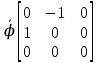
Пусть теперь
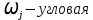 скорость j-ого тела, а телесные точки А* и В* движутся в плоскости движения Оxy. Пусть
скорость j-ого тела, а телесные точки А* и В* движутся в плоскости движения Оxy. Пусть 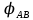 – угол, образуемый направленным отрезком
– угол, образуемый направленным отрезком 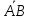 с положительным
с положительным 
направлением оси Ох.
Т.к.
 ≡0,
≡0, 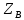 ≡0, то
≡0, то 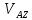 =0 и
=0 и 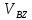 =0
=0Переход от А к В представим графом (1) А
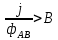
Подставим теперь в ф-лу Эйлера
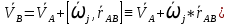
В матричной записи (2)
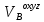 =
=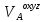 +
+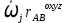
Здесь
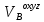 =
=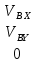 ,
, 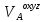 =
=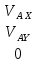 ,
, 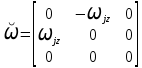 ,
, 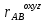 =
=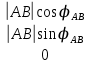
Переходя к компонентной записи из (2) получаем
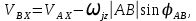
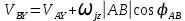 ,
,Эти формулы соответствуют графу (1).
Аналитический метод решения задач кинематики
Пример составного графа:
А
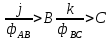
Распишем данный граф:
(1)
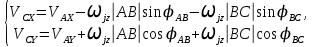
Соотношения (1) верны при следующем основном дополнении – скорости тех точек j-ого и k-ого тел, текущим положение которых служит т. В
Порядок решения типичных задач:
-
Выбрать кинематический граф, с которым связано не более 2-х неизвестных кинематических величин. -
Составить кинематические соотношения для выбранного графа. -
Учесть связи в концевых точках графа. -
Решить полученные кинематические ур-я. -
Если не все неизвестные найдены, вернуться к 1.
31. Решение задачи о разложении вектора на параллельную и ортогональную составляющие. Вычисление вектора угловой скорости по вектору относительной скорости при плоском движении.
Лемма: формула (*)
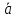 =(
=(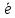 ,
,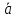 )
)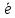 +[
+[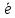 ,[
,[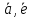 ]] дает разложение вектора
]] дает разложение вектора 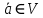 на 2 составляющие:
на 2 составляющие: параллельную и ортогональную заданному ед. вектору
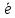
Док-во: проекция вектора
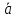 на направлении вектора
на направлении вектора 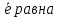 (
(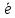 ,
,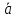 ) так, что
) так, что 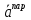 =(
=(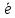 ,
,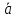 )
) 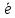
Применяем формулу «БАЦ» минус «ЦАП» для двойного векторного произведения
[
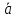 ,[
,[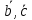 ]]=
]]=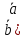 ,
,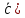 -
-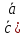 ,
,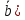 , получаем [
, получаем [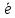 ,[
,[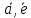 ]]=
]]=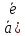 ,
,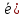 -
-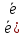 ,
,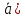 =
=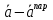 =
=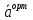
Найдем угловую скорость тела
 , если известны вектор
, если известны вектор 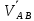 ≡
≡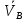 -
-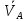
Запишем ф-лу Эйлера в виде (**)
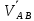 =[
=[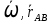 ]
]Разложим вектор
 на 2 составляющие: параллельную и ортогональную вектору
на 2 составляющие: параллельную и ортогональную вектору 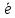 =
=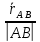
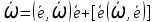 =
=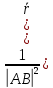 [
[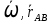 ]] в силу (**):
]] в силу (**):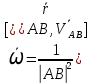 .
.Замечание: поскольку
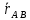 =(
=(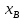 -
-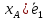 +(
+(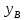 -
-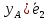 ,
, 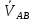 =(
=(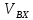 -
-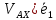 +(
+(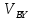 -
-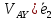 ,
,то
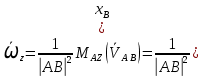 -
-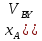 -
-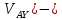 (
(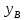 -
-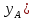 (
(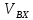 -
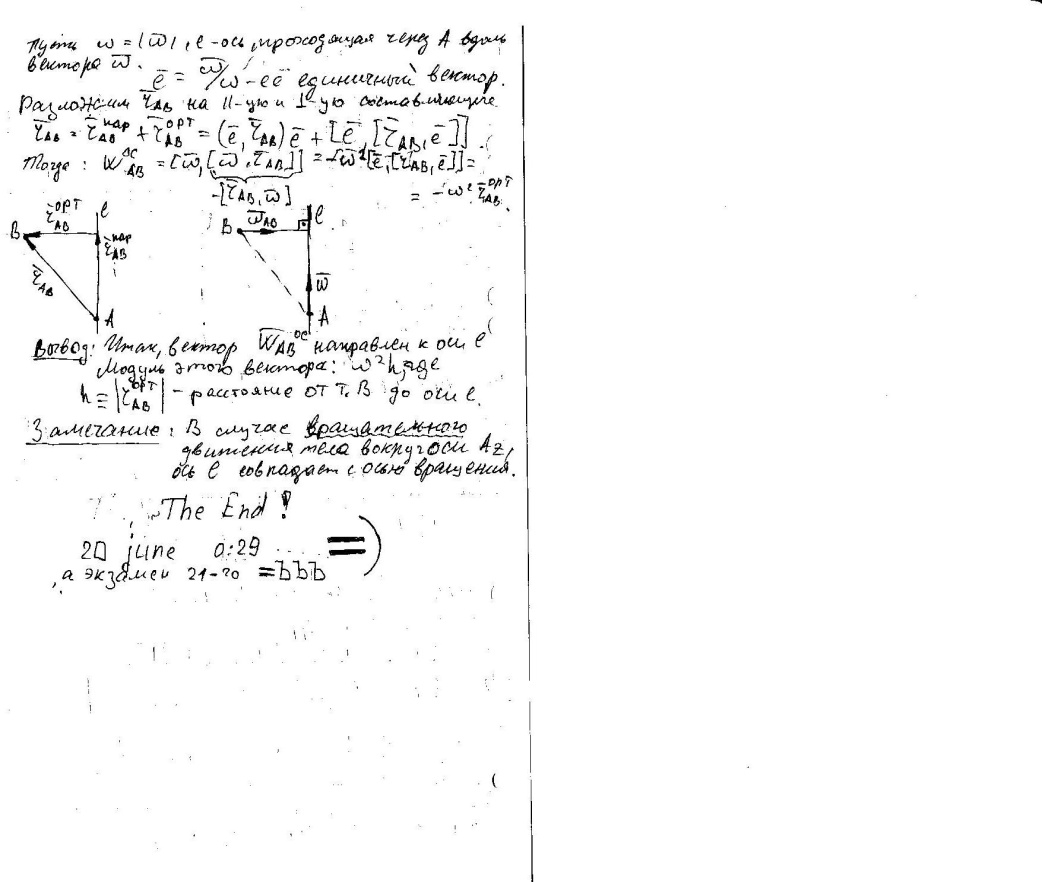
-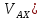 ]
]   |   |   |

