Файл: 18 Условие жёсткой связи неизменяемые мехе сисмы Конфигурация матго тела Теорема Грасгофа о проекциях скоростей.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 79
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Движение АТТ вращательное, если 2 телесные точки неподвижны. Пусть это точки О* и А*; обозначим через е* телесную прямую А*О*, а через ɭ текущее положение этой прямой в у. н. СО
Вращательное движение – частный случай сферического. Ось мгновенного вращения в любой момент проходит и через точку О и через А => она совпадает и прямой ɭ (осью вращения АТТ)
Вектор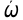 ll l ɭ
ll l ɭ
У любой точки оси вращения скорость тождественно равна 0, так что все точки оси вращения неподвижны.
Траектории любой телесной точки β* лежит на пересечении 2-х сфер с радиусами lOBl и lABl, т.е. на окружности с центром на оси вращения.
Траектории лежат в неподвижных плоскостях, ортогональных оси ɭ, ток что вращательное движение – частный случай плоского. Если ввести неподвижную систему координат Охуz, совместив ось z с осью ɭ, то плоскость Oxy можно
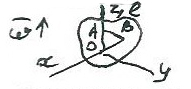
принять за плоскость движения.
Вывод: вращательное движение одновременно и сферическое и плоское.
27.Закон движения абсолютно твердого тела. Дифференцирование линейных операторов. Оператор угловой скорости; формула Эйлера в операторной записи.
Закон движения материального тела –правило, задающее для каждой точки тела и каждого момента времени текущее положение точки.
Прямой способ задания движения тела:
В=Н(В*;t);
конфигурация тела β зависит от t как от параметра, а В* β-произвольная точка тела
β-произвольная точка тела
Если тело β-абс. твердое, то В* Е*(т.е. это произвольная точка тела)
Е*(т.е. это произвольная точка тела)
Векторный способ: задают 2 ф-ции времени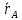 =
=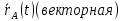 ;
;  =
= (t)(операторная);
(t)(операторная);
Здесь А- текущее положение полюса А*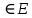 *, а
*, а  -оператор ориентации АТТ.
-оператор ориентации АТТ.
Тогда по основной ф-ие геометрии движения
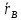 =
=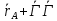 *, где
*, где  *=
*=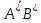 , можно найти закон движения произвольной телесной точки В*
, можно найти закон движения произвольной телесной точки В*
Если лин. оператор : х->у зависит от времени t, как от параметра:
: х->у зависит от времени t, как от параметра: 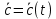 , то его производной по t наз-ся предел
, то его производной по t наз-ся предел 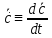 =
=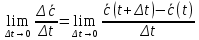
Пусть сущ. t оператор =
=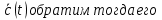 мультипликативной производной ( умножения) по t наз-ся лин. оператор:
мультипликативной производной ( умножения) по t наз-ся лин. оператор: 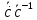 , т.к.
, т.к. 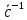 :-y->x, то
:-y->x, то 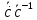 :y->y, т.е.
:y->y, т.е. 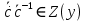
Оператор угловой скорости характеризует быстрому изменению ориентации АТТ формула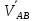 =
=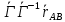 принимает вид
принимает вид 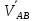 =
=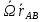 , т.к.
, т.к. 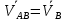 -
-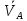 , получаем
, получаем
(*)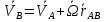
Это формула Эйлера( в операторной записи)
Вывод: мгновенное движение АТТ задано, если известны вектор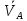 и оператор
и оператор 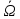 .
.
28.Теорема об антсимметричности оператора угловой скорости. Вектор угловой скорости; формула Эйлера в векторной записи. Траектории и скорости телесных точек при сфкрическом движении.
Теорема: оператор угловой скорости антисимметричный: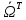 =-
=-
Док-во: в силу ортогональности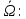
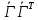 =
=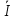 , дифференцируем по t
, дифференцируем по t 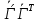 +
+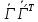 =0
=0
Вычисляем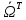 =
=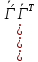 =
=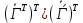 =
=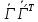 ,
, 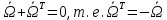
Вектор , сопоставляемый антисимметричному оператору
, сопоставляемый антисимметричному оператору  по формуле
по формуле 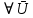
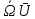 =[
=[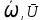 ] называется вектором угловой скорости АТТ.
] называется вектором угловой скорости АТТ.
Если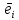 - един-ные векторы системы коорд. xyz, то
- един-ные векторы системы коорд. xyz, то  =
=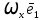 +
+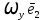 +
+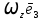 , а матрица
, а матрица 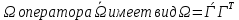 =
=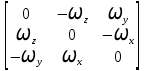
Вектор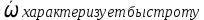 изменения ориентации АТТ
изменения ориентации АТТ
Это свободный вектор, т.к. его компоненты выражаются только через направление cos и их производных, а от выбора полюса не зависит
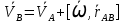 , это формула Эйлера в векторной записи, была получена в 1765 году.
, это формула Эйлера в векторной записи, была получена в 1765 году.
Движение АТТ сферическое, если одна из телесных точек неподвижна, поскольку текущее положение О этой точки О* не изменяется с течением времени, то О можно принимать за
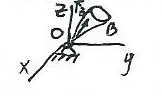
начало неподвижной системы координат.
Выберем точку О* за полюс, тогда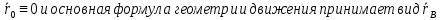 =
=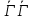 *, где
*, где  *=
*=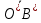
Вывод: соотношения =
= (t) определяет закон сферического движения тела
(t) определяет закон сферического движения тела
Из услвия IОВI=const следует, что траектории телесных точек при сферическом движении лежат на концентрических сферах
При сферическом движении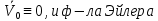 принимает вид (*)
принимает вид (*)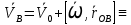
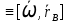 .
.
При сферическом движении АТТ:
-мгновенное движение в любой момент времени-мгновенное вращение, ось которого всегда проходит через точку О;
-распределение скоростей телесных точек задается формулой (*).
29.Плоское движение АТТ. Матрица направляющих косинусов при таком движении. Вывод соотношений для координат двух телесных точек при плоском движении.
Движение АТТ – плоское (или плоскопараллельное), если все телесные точки движутся в плоскостях, параллельных некоторой неподвижной плоскости (плоскость движется).
Траектории телесных точек при этом- плоские кривые.
Примем за плоскость движение Oxy ту из параллельных плоскостей, в которой движется полюс А*
Точки тела, движущегося в этой же плоскости, образуют плоскую фигуру.
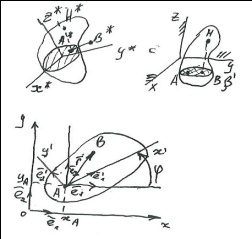
Вывод: Изучение плоского движения АТТ сводится к изучению движения плоской фигуры.
Здесь Аx’, Ay’,Az’-текущее положение осей А*х*, А*у*, А*z* (ось Az’ сонаправлена оси Оz)
Угол ϕ-угол поворота тела, отсчитывается от направляющей оси Ох до оси Ax’ в положительную сторону.
Перейдем у метрической записи основной формулы геометрии движения: =
= *, где
*, где  *=
*= .
.
Для чего введем столбцы: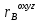 =
=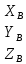 ,
, 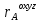 =
=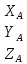 ,
, 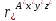 =
=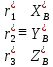
Получаем (*)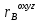 =
=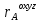 +
+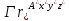
Сейчас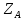 =0
=0
Напр. косинусов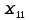 =cos(
=cos(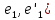 =cos ϕ
=cos ϕ
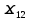 =cos(
=cos(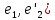 =-sin ϕ
=-sin ϕ
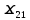 =cos(
=cos(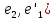 =sin ϕ
=sin ϕ
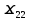 =cos(
=cos(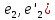 =cos ϕ
=cos ϕ
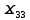 =cos(
=cos(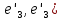 =cos 0=1
=cos 0=1
Остальные cos=0(векторы ортогональны)
Г=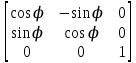 Вывод: соотношения
Вывод: соотношения 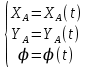 определяют закон плоского движения тела, при этом координаты т. В в силу (*) можно найти по формулам
определяют закон плоского движения тела, при этом координаты т. В в силу (*) можно найти по формулам
(**)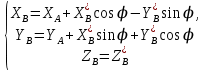
Для точек плоской фигуры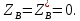
30.
Вращательное движение – частный случай сферического. Ось мгновенного вращения в любой момент проходит и через точку О и через А => она совпадает и прямой ɭ (осью вращения АТТ)
Вектор
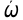 ll l ɭ
ll l ɭУ любой точки оси вращения скорость тождественно равна 0, так что все точки оси вращения неподвижны.
Траектории любой телесной точки β* лежит на пересечении 2-х сфер с радиусами lOBl и lABl, т.е. на окружности с центром на оси вращения.
Траектории лежат в неподвижных плоскостях, ортогональных оси ɭ, ток что вращательное движение – частный случай плоского. Если ввести неподвижную систему координат Охуz, совместив ось z с осью ɭ, то плоскость Oxy можно
принять за плоскость движения.
Вывод: вращательное движение одновременно и сферическое и плоское.
27.Закон движения абсолютно твердого тела. Дифференцирование линейных операторов. Оператор угловой скорости; формула Эйлера в операторной записи.
Закон движения материального тела –правило, задающее для каждой точки тела и каждого момента времени текущее положение точки.
Прямой способ задания движения тела:
В=Н(В*;t);
конфигурация тела β зависит от t как от параметра, а В*
 β-произвольная точка тела
β-произвольная точка телаЕсли тело β-абс. твердое, то В*
 Е*(т.е. это произвольная точка тела)
Е*(т.е. это произвольная точка тела)Векторный способ: задают 2 ф-ции времени
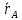 =
=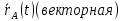 ;
;  =
= (t)(операторная);
(t)(операторная);Здесь А- текущее положение полюса А*
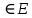 *, а
*, а  -оператор ориентации АТТ.
-оператор ориентации АТТ.Тогда по основной ф-ие геометрии движения
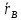 =
=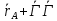 *, где
*, где  *=
*=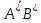 , можно найти закон движения произвольной телесной точки В*
, можно найти закон движения произвольной телесной точки В*Если лин. оператор
 : х->у зависит от времени t, как от параметра:
: х->у зависит от времени t, как от параметра: 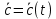 , то его производной по t наз-ся предел
, то его производной по t наз-ся предел 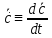 =
=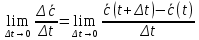
Пусть сущ. t оператор
 =
=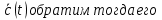 мультипликативной производной ( умножения) по t наз-ся лин. оператор:
мультипликативной производной ( умножения) по t наз-ся лин. оператор: 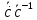 , т.к.
, т.к. 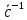 :-y->x, то
:-y->x, то 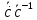 :y->y, т.е.
:y->y, т.е. 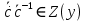
Оператор угловой скорости характеризует быстрому изменению ориентации АТТ формула
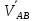 =
=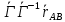 принимает вид
принимает вид 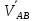 =
=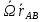 , т.к.
, т.к. 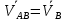 -
-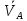 , получаем
, получаем (*)
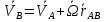
Это формула Эйлера( в операторной записи)
Вывод: мгновенное движение АТТ задано, если известны вектор
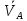 и оператор
и оператор 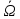 .
.28.Теорема об антсимметричности оператора угловой скорости. Вектор угловой скорости; формула Эйлера в векторной записи. Траектории и скорости телесных точек при сфкрическом движении.
Теорема: оператор угловой скорости антисимметричный:
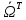 =-
=-
Док-во: в силу ортогональности
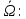
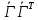 =
=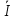 , дифференцируем по t
, дифференцируем по t 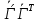 +
+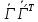 =0
=0Вычисляем
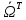 =
=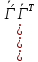 =
=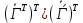 =
=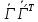 ,
, 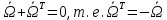
Вектор
 , сопоставляемый антисимметричному оператору
, сопоставляемый антисимметричному оператору  по формуле
по формуле 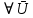
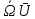 =[
=[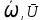 ] называется вектором угловой скорости АТТ.
] называется вектором угловой скорости АТТ.Если
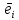 - един-ные векторы системы коорд. xyz, то
- един-ные векторы системы коорд. xyz, то  =
=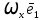 +
+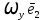 +
+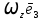 , а матрица
, а матрица 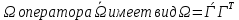 =
=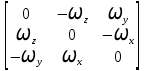
Вектор
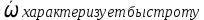 изменения ориентации АТТ
изменения ориентации АТТЭто свободный вектор, т.к. его компоненты выражаются только через направление cos и их производных, а от выбора полюса не зависит
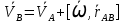 , это формула Эйлера в векторной записи, была получена в 1765 году.
, это формула Эйлера в векторной записи, была получена в 1765 году.Движение АТТ сферическое, если одна из телесных точек неподвижна, поскольку текущее положение О этой точки О* не изменяется с течением времени, то О можно принимать за
начало неподвижной системы координат.
Выберем точку О* за полюс, тогда
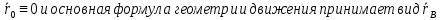 =
=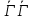 *, где
*, где  *=
*=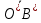
Вывод: соотношения
 =
= (t) определяет закон сферического движения тела
(t) определяет закон сферического движения телаИз услвия IОВI=const следует, что траектории телесных точек при сферическом движении лежат на концентрических сферах
При сферическом движении
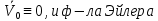 принимает вид (*)
принимает вид (*)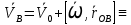
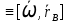 .
.При сферическом движении АТТ:
-мгновенное движение в любой момент времени-мгновенное вращение, ось которого всегда проходит через точку О;
-распределение скоростей телесных точек задается формулой (*).
29.Плоское движение АТТ. Матрица направляющих косинусов при таком движении. Вывод соотношений для координат двух телесных точек при плоском движении.
Движение АТТ – плоское (или плоскопараллельное), если все телесные точки движутся в плоскостях, параллельных некоторой неподвижной плоскости (плоскость движется).
Траектории телесных точек при этом- плоские кривые.
Примем за плоскость движение Oxy ту из параллельных плоскостей, в которой движется полюс А*
Точки тела, движущегося в этой же плоскости, образуют плоскую фигуру.

Вывод: Изучение плоского движения АТТ сводится к изучению движения плоской фигуры.
Здесь Аx’, Ay’,Az’-текущее положение осей А*х*, А*у*, А*z* (ось Az’ сонаправлена оси Оz)
Угол ϕ-угол поворота тела, отсчитывается от направляющей оси Ох до оси Ax’ в положительную сторону.
Перейдем у метрической записи основной формулы геометрии движения:
 =
= *, где
*, где  *=
*= .
.Для чего введем столбцы:
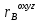 =
=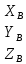 ,
, 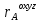 =
=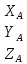 ,
, 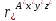 =
=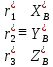
Получаем (*)
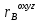 =
=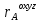 +
+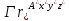
Сейчас
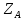 =0
=0Напр. косинусов
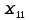 =cos(
=cos(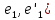 =cos ϕ
=cos ϕ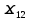 =cos(
=cos(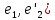 =-sin ϕ
=-sin ϕ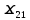 =cos(
=cos(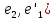 =sin ϕ
=sin ϕ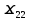 =cos(
=cos(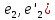 =cos ϕ
=cos ϕ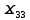 =cos(
=cos(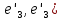 =cos 0=1
=cos 0=1Остальные cos=0(векторы ортогональны)
Г=
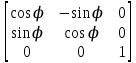 Вывод: соотношения
Вывод: соотношения 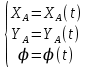 определяют закон плоского движения тела, при этом координаты т. В в силу (*) можно найти по формулам
определяют закон плоского движения тела, при этом координаты т. В в силу (*) можно найти по формулам(**)
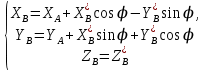
Для точек плоской фигуры
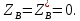
30.