Файл: 18 Условие жёсткой связи неизменяемые мехе сисмы Конфигурация матго тела Теорема Грасгофа о проекциях скоростей.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 81
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Уравнение траектории получается исключением t
4)Естественный- задают траекторию, начало отсчета, направление отсчёта, закон изменения линейной координаты
=
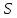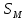(t)Из аксиомы движения следует, что любая из функций времени в 1)-4) непрерывна
13) Скорость точки в в-ом и координатном способах задания движения
Пусть t и
, 
=
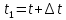(t)-текущий рад в-р. М и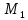 
положения т. 
в моменты t и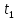 
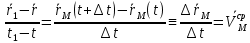средняя скорость т. на указ врем промеж
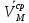направлена вдоль секущей. Придел 
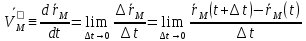-скорость т. в момент t, направлена по касательной к траекторииДля прямого способа
=
, 
, 
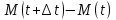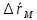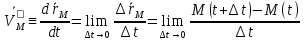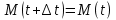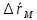
+ Из последней ф-лы для
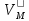следует, что она не зависит от выбора полюса ОИная запись
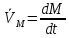
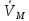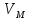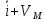(t)=
(t)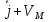
(t)
(t)
, дифференцируя по t р-во
(t)=
(t)
(t)
(t) получим 
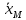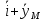(t)=
(t)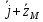
(t)
(t) , в координатном способе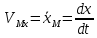 
и тд.Модуль скорости
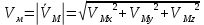
14)Скорость при естественном способе задания движения точки
Пусть траэктория точки- гладкая кривая и при t
[
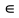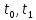] линейная координата S=
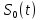монотонно меняется с изменением t, тогда можно выразить t, как ф-цию t=
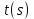, тогда можно выразить 
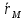представить, как сложную ф-цию 
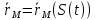тогда:(*)
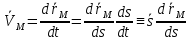Обозначим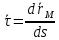 
Заметим что
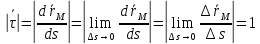
Итак
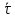еденичный касательный в-р; он направлен вдоль траэктории, в направлении роста S. Из ф-лы (*) получаем: (**)
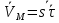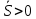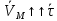(при 
, 
, при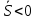 
, 
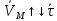)Скалярная величина
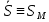
алгебраическая скорость Т(мгновенная алгебраическая скорость),
; 
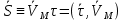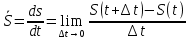под знаком Lim-средняя алгебраическая скорость на t
[
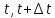]Следствие(Эйлера)-модуль скорости точки = модули её алгебраической скорости
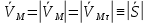Значит 
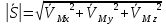, так как 
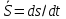, то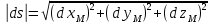
Формула Клеро для дыф-ла линейной координаты17)Лемма об уравнениях сближения двух точек по экспоненте
Пусть т
и 
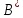сближаются по экспоненте:(1)
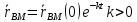, те 
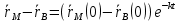при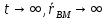 
В силу (1) линия визирования MB остаётся || первоначальному направлению => || сближение. Если движение в плоскости Oxy, то
(
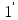) x=x(0)
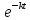, y=y(0)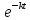 Точки
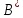и сближаются по экспоненте их скорости удовлетворяют уравнениям сближения по экспоненте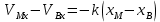
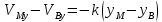
Док-во: 1) Пусть точки сближаются по экспоненте, дифференцируя (1) по t
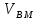=-k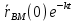
Итак,
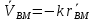, в координатной записи это сводится к (*)2) Пусть ур-я (*) выполнены, представим их в виде
(**)
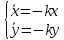
Поставив для системы дифур (**) задачу Кош(нач условия x(0)=
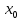, y(0)=
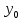)Прямой подстановкой (1’) в (**) убеждаемся что ф-лы(1’) дают решение поставленной задачи Коши
x(0)(-k)
=-kx(0) y(0)(-k)
=-ky(0) В силу (1’) т.
и 
сближаются по экспоненте3)Сис-мы сил и их эквивалентность. Главный вектор и главный момент сис-мы сил. Теорема об изм-ии гл. момента при смене полюса.
Системой сил {
.
,…,
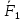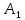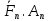} называется совокупность сил,приложенных к точкам одного и того же атт.Система сил сходящаяся если линии действия всех сил пересек. в 1 точке. Силы образуют систему парал. Сил если линии их действия парал. Система сил плоская если линии действия всех сил лежат в одной плоскости. Эквивалентность-это равенство по отношению к некоторым выделенным признакам. Три обязательных требования к эквивалентности:1)рефлексивность2)семмертичность3)транзитивность
Две системы сил называются экв. Если одно из них можно заменить другой не нарушая состояния покоя или движения атт. Если система сил будучи приложенной к атт не нарушает состояния покоя то она наз уравновешенной. Главный вектор системы сил- свободный вектор равный сумме векторов всех сил системы. Главный момент системы сил относ. Полюса В -вектор,прилож. в т.В и равный сумме моментов всех сил системы относ. данного полюса.
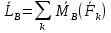
Теорема.
Главный момент системы сил относительно нового полюса О получается если к главному моменту системы сил относ. старого полюса В прибавить слагаемое
(*)
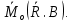
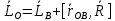
Обозначим
, 
= 
. = 
+ 
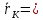
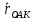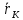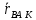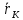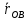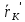тогда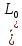 
=
=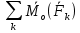