Файл: 18 Условие жёсткой связи неизменяемые мехе сисмы Конфигурация матго тела Теорема Грасгофа о проекциях скоростей.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 80
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
y: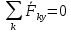
z:
:
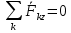
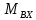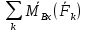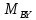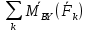=0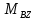 
:
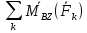=0 
:
=0
Для системы из n тел получаем 6 n уравнений равновесия.
9)Ур-е равновесия для плоской и сходящейся сис-мы сил, для сис-мы параллельных сил. Статистически определяемые задачи.
Уравнения равновесия АТТ
1)Пусть система сил-плоская и полюс В вместе с осями x и y лежит в той же плоскости что и сила. Тогда можно пользоваться ур-ми: X:
y: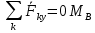
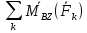: =0 В самом деле ɏ К 
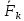перп
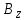и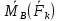 
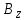// ,т.ч остальные 3 ур-ия обратились в тождества.
2) Пусть система сил-параллельная, тогда ɏ К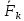 // 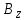,тогда можно пользоваться ур-ми: z: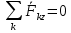
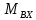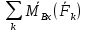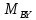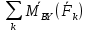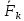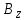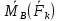: =0 : =0 В самом деле ɏ К // и перп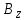
3) ) Пусть система сил-сходящаяся и линии действия всех сил проходят через В. Тогда можно пользоваться ур-ми: X: y:
z:
Для ɏ К 
=0
Задача статистически определима если число неизвестных не превосходит числа ур-ий равновесия. Если в задаче nтел и m неизвестных то в статист опр задачах:m≤3n-плоский случай;m≤6n-простр-ый случай.
11)Законы трения скольжения(при покое). Закон Амантона-Кулона. Задача о трибометре.
Законы трения скольжения:
1)Если тело на которое действует сила трения скольжения находится в покое то модуль ее может принимать любое значение. Случай предельного равновесия-модуль силы тр=макс силе тр
2)Предельная величина силы трения прямопропорциональна модулю нормальной реакции
3)Значение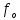
не зависит от площади соприкосновения
4) Значение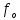 зависит материала тел, частоты обработки пов-ей и т.п
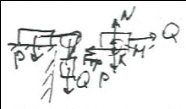
Задача о трибометре.
X:Q-
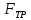=0 Q=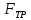 y:N-P=0 N=P Подбором груза находим наибольшее значение Q при котором брусок будет покоится. В силу закона Амонтона-Кулона:
макс 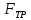= 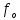N так что 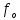=: макс 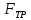/N= Qмакс/Р
26. Антисимметричные линейные операторы. Теорема о взаимно однозначном соответствии между векторами и антисимметричными операторами в трехмерном пространстве.
Пусть х-евклидово векторное пр-во. Линейный оператор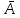
– антисимметричный, если (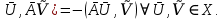
В общем случае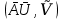
=(
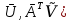. Иная форма определения: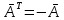 
Для компонентов антисимметричного оператора
в ортонорм. Базисе 
≡
=-
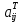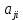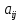
Значит, матрица А оператора тоже антисимметрична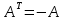
В частности, при i=j: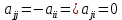
Пусть Z(x) –пр-во всех линейных операторов вида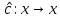
Присоединенным представлением алгебры векторов 3-х мерного пр-ва Vназывается отображение : аd: V->Z(V), которое всякому вектору ā сопоставляет лин. Оператор , определяемый формулой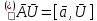 
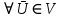
Линейность оператора следует из равенств
[
=
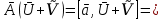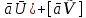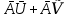
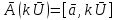=k[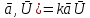
Оператор ≡ad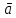 
будем обозначать ă и называть присоединительным оператором для вектора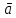
Теорема: отображение ad: :V->Z(V) устанавливает взаимно-однозначное соответствие между векторами из V и антисимметричными линейными операторами:
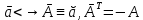
Док-во: в силу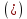
линейный оператор , отвечающий вектору
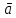
, определен однозначно. Проверим, что он антисимметричный.
Пусть {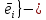
правый ортонорм. базис в V, тогда 
=
=>
=>
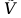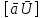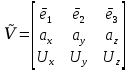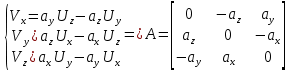, так что 
,
так как , то и 
Взаимная однозначность всякий оператор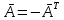
в 3-х мерном пр-ве имеет матр. А указанного вида; поэтому вектор 
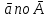находится однозначно.
Замечание: в силу взаимной однозначности установленного соответствия для всякого антисимметричного оператора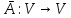
однозначно определен вектор 
= a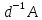
, для которого ă=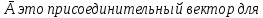
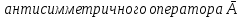
Следствие 1: ă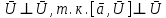
Следствие 2: ă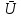
=0 II , т.к. 
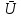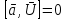
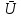II
Следствие 3: т.к. операторă все векторы, параллельные переводит в 0, то антисем. Операторы в 3-х мерном пр-ве необратимы(обратного оператора не сущ.)
Вывод: в 3-х мерном пр-ве операции умножения вектора на антисим. оператор эквивалентно операции векторного умножения.
32. Вращательное движение абсолютно твердого тела. Ось вращения. Траектории и скорости телесных точек при вращательном движении.
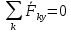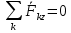
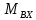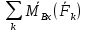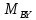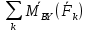z: : =0 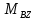: 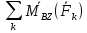=0 : =0Для системы из n тел получаем 6 n уравнений равновесия.
9)Ур-е равновесия для плоской и сходящейся сис-мы сил, для сис-мы параллельных сил. Статистически определяемые задачи.
Уравнения равновесия АТТ
1)Пусть система сил-плоская и полюс В вместе с осями x и y лежит в той же плоскости что и сила. Тогда можно пользоваться ур-ми: X:
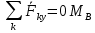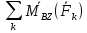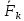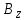y: : =0 В самом деле ɏ К перп и 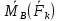// 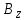,т.ч остальные 3 ур-ия обратились в тождества.2) Пусть система сил-параллельная, тогда ɏ К
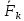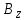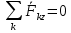
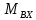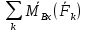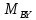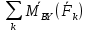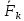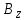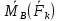// ,тогда можно пользоваться ур-ми: z: : =0 : =0 В самом деле ɏ К // и перп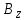
3) ) Пусть система сил-сходящаяся и линии действия всех сил проходят через В. Тогда можно пользоваться ур-ми: X:
y: z: Для ɏ К =0Задача статистически определима если число неизвестных не превосходит числа ур-ий равновесия. Если в задаче nтел и m неизвестных то в статист опр задачах:m≤3n-плоский случай;m≤6n-простр-ый случай.
11)Законы трения скольжения(при покое). Закон Амантона-Кулона. Задача о трибометре.
Законы трения скольжения:
1)Если тело на которое действует сила трения скольжения находится в покое то модуль ее может принимать любое значение. Случай предельного равновесия-модуль силы тр=макс силе тр
2)Предельная величина силы трения прямопропорциональна модулю нормальной реакции
3)Значение
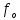не зависит от площади соприкосновения 4) Значение
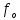зависит материала тел, частоты обработки пов-ей и т.п Задача о трибометре.
X:Q-
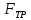=0 Q=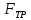 y:N-P=0 N=P Подбором груза находим наибольшее значение Q при котором брусок будет покоится. В силу закона Амонтона-Кулона: макс 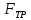= 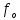N так что 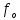=: макс 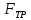/N= Qмакс/Р26. Антисимметричные линейные операторы. Теорема о взаимно однозначном соответствии между векторами и антисимметричными операторами в трехмерном пространстве.
Пусть х-евклидово векторное пр-во. Линейный оператор
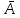– антисимметричный, если (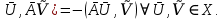 В общем случае
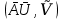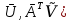=( . Иная форма определения: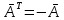 Для компонентов антисимметричного оператора
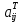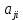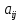
в ортонорм. Базисе ≡ =- Значит, матрица А оператора
тоже антисимметрична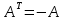 В частности, при i=j:
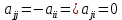
Пусть Z(x) –пр-во всех линейных операторов вида
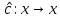
Присоединенным представлением алгебры векторов 3-х мерного пр-ва Vназывается отображение : аd: V->Z(V), которое всякому вектору ā сопоставляет лин. Оператор
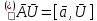
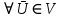
, определяемый формулой Линейность оператора
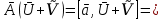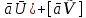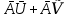
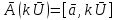следует из равенств [ = =k[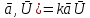 Оператор
≡ad 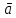будем обозначать ă и называть присоединительным оператором для вектора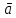 Теорема: отображение ad: :V->Z(V) устанавливает взаимно-однозначное соответствие между векторами из V и антисимметричными линейными операторами:
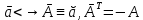
Док-во: в силу
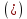линейный оператор , отвечающий вектору
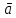
, определен однозначно. Проверим, что он антисимметричный.
Пусть {
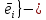правый ортонорм. базис в V, тогда 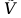= =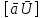> =>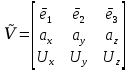 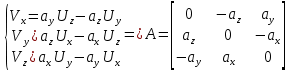, так что ,так как
, то и Взаимная однозначность всякий оператор
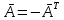в 3-х мерном пр-ве имеет матр. А указанного вида; поэтому вектор 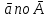находится однозначно.Замечание: в силу взаимной однозначности установленного соответствия для всякого антисимметричного оператора
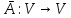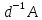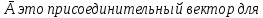
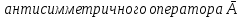
однозначно определен вектор = a , для которого ă= Следствие 1: ă
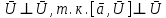
Следствие 2: ă
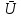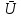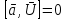
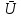=0 II , т.к. II Следствие 3: т.к. операторă все векторы, параллельные
переводит в 0, то антисем. Операторы в 3-х мерном пр-ве необратимы(обратного оператора не сущ.)Вывод: в 3-х мерном пр-ве операции умножения вектора на антисим. оператор эквивалентно операции векторного умножения.
32. Вращательное движение абсолютно твердого тела. Ось вращения. Траектории и скорости телесных точек при вращательном движении.