Файл: 18 Условие жёсткой связи неизменяемые мехе сисмы Конфигурация матго тела Теорема Грасгофа о проекциях скоростей.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 78
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
18) Условие жёсткой связи; неизменяемые мех-е сис-мы; Конфигурация мат-го тела; Теорема Грасгофа о проекциях скоростей.
- Жесткая связь(наложенная на точки А и В ϵ S’)
В этом случае в любом движении сис-мы выполнено условие:
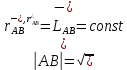
Смысл его: расстояние между текущими положениями точек остаётся постоянным.
Иная форма записи условия жёской связи: (**)
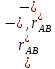 )=
)=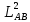
В координатах:
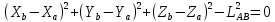 .
.-Механическая система – неизменяемая, если расстояния между положениями 2-х её точек остаются постоянными, каким бы воздействиям она не подвергалась
Частые случаи: 1. Неизменяемая СМТ. 2. Абс. Твёрдое тело(АТТ)
Если B – мат. тело, то в момент времени t положение его точек непрерывно заполняют(по аксиоме сплошности) в у.н. СО ε некоторую область
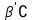 ε
εОтображение Н:
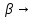 ε сопоставляющее каждой точке тела её текущее положение в у.н. СО, называется конфигурацией тела
ε сопоставляющее каждой точке тела её текущее положение в у.н. СО, называется конфигурацией тела 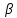 (в текущий момент времени
(в текущий момент времениОна задана, если указано правило, по кот-му можно найти текущее положение любой точки тела.
Если А,В – текущие положения точек А* и В* тела
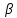 , то это означает: А=Н(А*), В=Н(В*)
, то это означает: А=Н(А*), В=Н(В*)Условие вида (**) должно выполняться для любых 2-х точек неизменяемое сис-мы (будучи либо усл. Одной из связей, либо следствием из усл. Других связей).
-Теорема Грасгофа о проекциях скоростей.
Если на точки А* и В* наложена жесткая связь, то проекции их скоростей на прямую, соединяющую текущие положенияэтих точек равны:
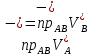
Д-во: достаточно доказать, что:
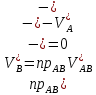
Диф-я по t условие жёской связи
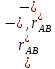 )=const, получаем (
)=const, получаем (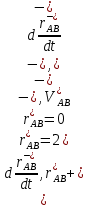
Итак,
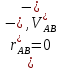 , т.е.
, т.е. 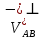
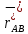
Пусть теперь
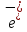 - ед. вектор оси АВ. Имеем:
- ед. вектор оси АВ. Имеем: 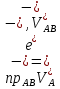 =
=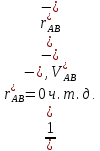
Замечание: т-ма Грасгофа верна для точек неизменяемой сис-мы(в частности АТТ).
19)Допустимые конфигурации мех. сис-м;Коллинеарные точки неизменяемой мех. сис-мы; Теорема о скоростях коллин. точек.
Конфгурация мех. сис-мы допустимая, если:
-положения всех точек сис-мы удовлетворяют намеченным на неё геом. связям(осн. требование)
-данную конфигурацию можно получить из отсчётной непрерывным движением, не нарушающим связей(доп. требование)
Покажем, что если для какой-либо конфигурации неизменяемой сис-мы текущие положения её точек А*, В*, С* коллинеарны(лежат на одной прямой), то и для любой допустимой конфигурации они будут коллинеарны.
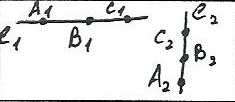
В самом деле, если бы
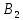 не лежала на прямой
не лежала на прямой 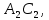 то было бы:
то было бы:|
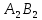 |+|
|+|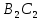 |>|
|>|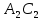 |=|
|=|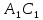 |=|
|=|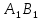 |+|
|+|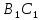 |
|В случае неизменяемой сис-мы считаем, что точки: Коллинеарны, если коллин. их положения
Теорема о скоростях коллин. точек.
Концы скоростей точек неизм. сис-мы, лежащих на одной прямой, также лежат на одной прямой и делят её на части пропорциональные расстояниям между точками
Док-во: зафиксируем ед. изм-я времени, выбрав масштаб для геометр. Изображения скоростей.
Дифференцируем (*) по t, получим (**)
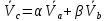
Складывая(*) и (**) получаем:
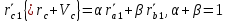
Значит
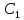 лежит на прямой
лежит на прямой 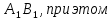
|
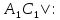 |
|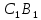 |=
|=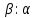 =|AC|:|CB| ч.т.д.
=|AC|:|CB| ч.т.д.20)Основное св-во допустимой конфигурации абсолютно тв. тела; Задание конфигурации тв. тела методом 3-х точек.
-метод 3-х точек:
В данном методе в теле выбирают неколлинеарные точки А*,В*,С*.
Конфигурацию АТТ задают, указав текущие положения этих точек: А=Н(А*), В=Н(В*), С=Н(С*)
Здесь Н:
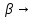 C – конфигурация АТТ
C – конфигурация АТТВектор
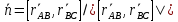 является таким вектором нормали в плоскости АВС, что с его конца обход
является таким вектором нормали в плоскости АВС, что с его конца обход виден происходящим против часовой стрелки.
виден происходящим против часовой стрелки.-Основное св-во доп. конфигурации АТТ – она сохраняет расстояние между его точками. Поэтому должны выполняться требования:
|AB|=|A*B*|,|CA|=|C*A*|,|BC|=|B*C*|
21)Связанная сис-ма отсчёта. Задание конфигурации АТТ методом связанных осей. Нахождение текущего положения телесной точки по её координатам в связанных осях.
-метод связанных осей:
Рассмотрим отсчётную конфигурацию АТТ. Пусть D
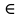 ε не принадлежит области
ε не принадлежит области 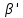 , занимаемой точками тела. Можно считать, что D явл. Положением воображаемой т. D*, жестко связанной с телом
, занимаемой точками тела. Можно считать, что D явл. Положением воображаемой т. D*, жестко связанной с телом 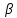 , тогда при любом движении тела D* будет двигаться вместе с телом (т.е. расстояние между ее положением и положением любой точки тела меняться не будет).
, тогда при любом движении тела D* будет двигаться вместе с телом (т.е. расстояние между ее положением и положением любой точки тела меняться не будет).Значит, зная расстояния |A*D*|,|B*D*|,|C*D*| от D* до 3-х заранее выбранных неколлин. Точек тела можно в любой его конфигурации найти положение данной точки.
-Связанная сис-ма отсчёта ε* - геометрически тв. среда, жестко связанная с данным АТТ, кот-е в ней покоится.
-Задание конфигурации тв. тела методом связанных осей
В методе связ. осей в СО ε* выбирают координатные оси A*, x*, y*, z*; конфигурацию АТТ задают, указав текущее расположение подвижных осей Ax', y', z', для чего достаточно указать А=Н(А*) и 3 единичных вектора
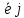 . Таким, что это позволяет найти текущее положение в любой телесной т. В*
. Таким, что это позволяет найти текущее положение в любой телесной т. В*Разложим векторы
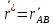 и
и 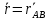 по базисам {
по базисам {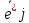 } и {
} и {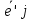 }
} 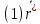 =
= 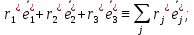
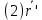 =
= 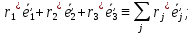
В силу основного св-ва допустимой конфигурации АТТ, коэф-ты
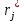 (1) и (2) совпадают.
(1) и (2) совпадают.При этом
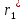 =
=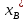 ,
, 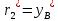 ,
, 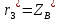 , т.е. это координаты точки В*
, т.е. это координаты точки В*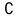 ε* в сис-ме A*x*y*Z*
ε* в сис-ме A*x*y*Z*Пусть теперь О – полюс в ε, а
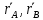 – радиус-вектора т.А и В. Поскольку
– радиус-вектора т.А и В. Поскольку 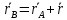 , то в силу (2) (*)
, то в силу (2) (*) 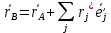
Вывод: текущая конфигурация АТТ определена однозначно, если заданы:
1)
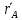 (задающий текущее положение полюса А*)
(задающий текущее положение полюса А*)2) векторы
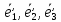
22)Оператор ориентации абсолютно твёрдого тела. Ортогональность оператора ориентации. Основная формула геометрии движения.
- Оператор ориентации
Пусть телесные точки M*,N*,P*,Q* образуют параллелограмм, а Н: ε*
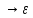 - текущая конфигурация АТТ. Она сохраняет длины отрезков, а поэтому текущие положения M,N,P,Q данных точек тоже образуют параллелограмм, геометрически равный исходному.
- текущая конфигурация АТТ. Она сохраняет длины отрезков, а поэтому текущие положения M,N,P,Q данных точек тоже образуют параллелограмм, геометрически равный исходному.При переходе от телесных точек к их положениям, для направленных отрезков соханяются:
- длины: (1)|M*N*|=|MN|;
- углы между ними: (2)
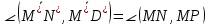
- их суммы: (3)
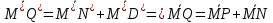
-их произведения на скаляры: (4) )
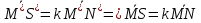
-отн-е геом. равенства: (5)
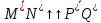 =>
=>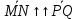
-Ортогональность
Из (1) и (2)=>|
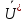 |=|
|=|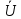 |,
|, 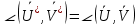 , но тогда и
, но тогда и 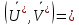 |
|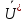 |*|
|*|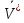 |*cos
|*cos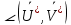 = |
= |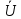 |*|
|*|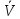 |* cos
|* cos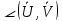 =
= 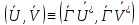
Если пространство Х,Y – Евклидово, а лин. опер.
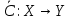 сохраняет скалярное произведение
сохраняет скалярное произведение 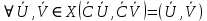 , называется ортогональным.
, называется ортогональным.Вывод: Оператор ориентации
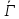 - ортогональный оператор.
- ортогональный оператор.-Основное ур-е геометрии движения:
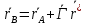
23)Поступательное движение тв. тела. Теорема о критерии поступательного движения. Траектории, скорости и ускорения телесных точек при поступательном движении.
Движение прямой линии(или отрезка) – поступательное, если она(он) всё время сохраняют параллельность своему первоначальному направлению.
Движение АТТ – поступательное, если любая прямая, жестко связанная с телом движется поступательно
-Теорема о критерии поступательного дв-я
Для того, чтобы движение АТТ было поступательно, необходимо и достаточно, чтобы оператор ориентации тела оставался постоянным:
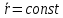
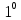 . АТТ движется поступательно => связанные координатные оси А*х*, А*y*, A*z* движутся поступательно, поэтому вектора осей
. АТТ движется поступательно => связанные координатные оси А*х*, А*y*, A*z* движутся поступательно, поэтому вектора осей 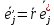 сохраняют свои направления неизменными. Значит,
сохраняют свои направления неизменными. Значит, 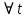
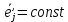 , но тогда при отнесении к у.н.СО любого свободного телесного вектора
, но тогда при отнесении к у.н.СО любого свободного телесного вектора 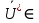
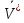 имеем:
имеем: 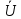 =
=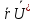 (где
(где 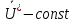 ), а поэтому и
), а поэтому и 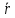 =const
=const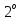 Если
Если 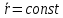 , а e*- произвольная телесная прямая с ед. вектором
, а e*- произвольная телесная прямая с ед. вектором 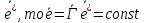 , т.е. прямая движется поступательно. ч. т. д.
, т.е. прямая движется поступательно. ч. т. д.При поступательном движении Траектории телесных точек – параллельные кривые: они получаются из траектории А* параллельным переносом.
При поступательном движении скорости и ускорения всех телесных точек одинаковы.
24)Компоненты и матрица линейного оператора; формулы для компонент линейного оператора. Матрица направляющих косинусов тв. тела.
Пусть
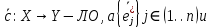 {
{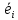 }
} 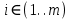 – базисы в X и Y
– базисы в X и YКоэффициенты
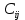 в расположении
в расположении 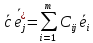 называются компонентами оператора
называются компонентами оператора 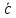 , а составленная из этих компонент матрица с – матрица данного оператора.
, а составленная из этих компонент матрица с – матрица данного оператора.Если пр-во Х и Y евклидовы, а базисы
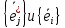 - ортонормированные, то
- ортонормированные, то(*)
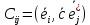
Это следует из ф-лы
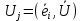 для i-той компоненты вектора
для i-той компоненты вектора 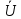 в ортонормированном базисе.
в ортонормированном базисе.Пусть А*х*у*Z* - сис-ма координат в СО, связанной с АТТ
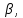 а охуz – неподвижные оси координат
а охуz – неподвижные оси координатДля компонент
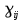 оператора ориентации
оператора ориентации 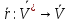 имеем:
имеем: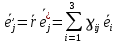 ; здесь{
; здесь{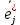 }- связанный базис, {
}- связанный базис, {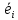 } – неподвижный базис, а
} – неподвижный базис, а 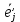 - единичные векторы подвижных осей Ах'y'z' (т.е. осей A*x*y*z*, отнесённых к у.н. СО)
- единичные векторы подвижных осей Ах'y'z' (т.е. осей A*x*y*z*, отнесённых к у.н. СО)В силу (*):
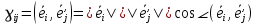
Компоненты
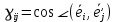 оператора ориентации, иначе именуются Направляющими косинусами осей x'y'z' по отношению к осям xyz, а его матрицу
оператора ориентации, иначе именуются Направляющими косинусами осей x'y'z' по отношению к осям xyz, а его матрицуГ
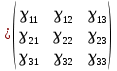 называют Матрицей направляющих косинусов тела
называют Матрицей направляющих косинусов тела 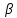 .
.25)Транспонирование линейных операторов. Св-ва матрицы направляющих косинусов.
Пусть
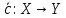 , а пр-ва X,Y – евклидовы. Оператор
, а пр-ва X,Y – евклидовы. Оператор 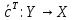 называется транспонированным оператором для оператора
называется транспонированным оператором для оператора 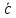 , если
, если 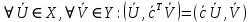
Имеем:
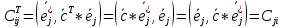
Вывод: матрица
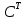 транспонированного оператора
транспонированного оператора 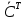 получается из матр. С оператора
получается из матр. С оператора 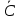 транспонированым.
транспонированым.Св-ва матрицы напр-х косинусов:
1)Матр. Напр. Кос. Г – собственная ортогональная:
-
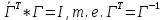
- det Г = 1 (определитель)
2) у матр. Г:
- скалярный квадрат каждого столбца(строки) = 1
- скалярные произведения разных столбцов(строк) = 0.
1)Момент силы относительно точки
Момент силы относительно полюса В-вектор приложенный в т.В и = векторному произв радиус вектора т. приложения на вектор силы:
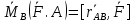 Основны с-ва вытекают из с-в в-во умножения
Основны с-ва вытекают из с-в в-во умноженияСвойства:
1)Переход от силы к её моменту-линейная операция
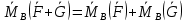 ,если силы F и G прилож в одной т.
,если силы F и G прилож в одной т. 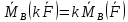
2)Модуль момента силы определяется ф-лой
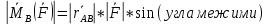
3)Направление момента силы определяется условиями
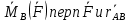 , и в-ры
, и в-ры 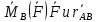
Образуют правую тройку в-ов
4) Линия действия силы – прямая, проходящая в направлении силы через точку её приложения
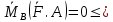 полюс В лежит на линии действия силы. Момент силы хорактерезует вращательный эффект силы
полюс В лежит на линии действия силы. Момент силы хорактерезует вращательный эффект силыПлечо силы - кратчайшее расстояние от полюса до линии действия силы
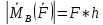
2)Вычисление проекции момента силы. Антисимметричные матрицы. Момент силы относительно оси
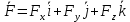 , где
, где 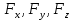 -компоненты в-ра
-компоненты в-ра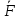 в осях Oxyz;
в осях Oxyz;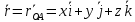 , где x,y,z- координаты т.А в осях Oxyz
, где x,y,z- координаты т.А в осях OxyzМомент силы
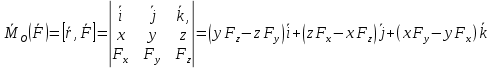
Компоненты в-ра
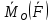 в осях Oxyz
в осях Oxyz(*)
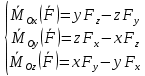
Введём столбцы компонент в-ов
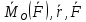
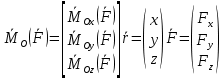 р-во сводится к одному матричному р-ву
р-во сводится к одному матричному р-ву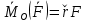 , если
, если 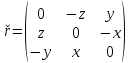 , матрица
, матрица 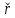 антисимметрична
антисимметрична Последнюю ф-лу (*) можно представить в виде (**)
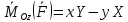 - Ф-ла Пуансо, тк в неё не входит z, след проэкция момента ситы на ось не изменится, при сдвиге полюса вдоль этой оси.
- Ф-ла Пуансо, тк в неё не входит z, след проэкция момента ситы на ось не изменится, при сдвиге полюса вдоль этой оси.
Момент силы относительно оси- скалярная величина = проекции на эту ось момента силы относительно точки, лежащей на данной оси. Можно вычислить проэцируя р-ро на ось BZ
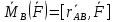 , вместо последней ф-лы(*)
, вместо последней ф-лы(*)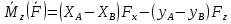
4)Аксиомы статики: общие аксиомы о силах. Следствие о переносе силы вдоль линии действия
1)Аксиома параллелограмма сил
Состояние тела не нарушится, если 2 силы, приложенные в одной точке заменить их геометрической суммой
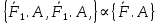 , где
, где 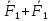 =
=
2)Аксиома о нуль системе
Состояние нуль системе не изменится, если к действующей на него системе сил добавить(отбросить) нуль систему
Тело на движение которого не наложено никаких наперед заданных ограничений называется свободным.
3) Свободное АТТ под действием двух сил находится в равновесии тогда и только тогда, когда эти силы: Равны по модулю, противоположны по направлению, лежат на одной прямой (
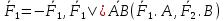 ) –элементарная нуль система
) –элементарная нуль системаСледствие(о переносе силы вдоль линии действия)
Силу приложенную к АТТ можно переносить вдоль линии действия в любую точкуне меняя состояния тела
Док-во
Пусть к телу приложена
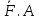 , а B лежит на её линии действия. Приложим к телу также
, а B лежит на её линии действия. Приложим к телу также 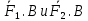 :
: 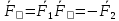 ,
, 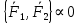 по аксиоме 3;
по аксиоме 3; 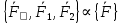 по акс2
по акс2Итак {
 }
}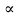
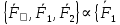 }, те
}, те 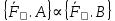
Вывод: Силу приложенную к АТТ, можно рассматривать как скользящий вектор. 2и 3 аксиомы применимы только к АТТ.
4)Аксиома о действии и противодействии:
Если на тело 1 с силой
 воздействует тело 2, то на тело 2 со стороны тела 1 действует сила
воздействует тело 2, то на тело 2 со стороны тела 1 действует сила 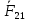 , причём эти силы: Равны по модулю, противоположны по направлению, лежат на одной прямой.
, причём эти силы: Равны по модулю, противоположны по направлению, лежат на одной прямой.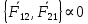 тк они приложены к разным телам
тк они приложены к разным телам10)Условия равновесия твёрдого тела при наличии трения(точечный и поверхностный контакт)
Возможные перемещения при наличии трения те же что и при его отсутствии
Если трение имеется, то при отбрасывании данной связи её действие заменяется силой
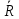 .K и парой сил с моментом
.K и парой сил с моментом 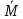 . Проекция реакции R на внешнюю нормаль неотрицательна, трение препятствует движению не не запрещает его. Разложив всё на касательную и нормальную составляющие получим: N-нормальная составляющая реакции, Fтр- трение скольжения(препятствует скольжению), Mкач- момент тр. качения, Mверч- момент тр. Верч(препятствует вращению вокруг внешней нормали)
. Проекция реакции R на внешнюю нормаль неотрицательна, трение препятствует движению не не запрещает его. Разложив всё на касательную и нормальную составляющие получим: N-нормальная составляющая реакции, Fтр- трение скольжения(препятствует скольжению), Mкач- момент тр. качения, Mверч- момент тр. Верч(препятствует вращению вокруг внешней нормали)Условие равновесия
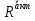 +
+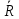 =0,
=0, 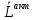 +
+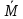 =0, где
=0, где 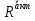 и
и 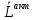 главный вектор и главный момент активной силы. Разложив их получим
главный вектор и главный момент активной силы. Разложив их получим 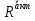 =
=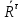 +
+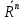 ,
, 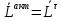 +
+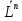 Вывод: при равновесии в примере 1 имеем (*)
Вывод: при равновесии в примере 1 имеем (*)
 тр=-
тр=- ,
, 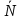 =-
=- , Mкач=-
, Mкач=-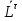 , Mверч=-
, Mверч=- . Условие (*) необходимое но не достаточное. Для равновесия необходимо (**) |
. Условие (*) необходимое но не достаточное. Для равновесия необходимо (**) | тр|<= Fтрмах,|
тр|<= Fтрмах,| кач |<= Mкачмах, |
кач |<= Mкачмах, |  верч |<= Mверчмах
верч |<= MверчмахСухое - тр в отсутствии смазки
Вязкое - тр при наличии смазки
12) Способы задания движения точки
В кинематике точки изучаются движения как мат. Тел, так и отдельных точек этих тел
Способы задания:
1)Прямой – текущее положение M т.
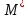 задана как ф-ция времени M=M(t)
задана как ф-ция времени M=M(t)2)Векторный- радиус вектор текущего положения точки задан как ф-ция времени
 =
=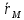 (t), относительно полюса О.
(t), относительно полюса О.3)Координатный- координаты заданы как ф-ции от времени
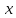 =
=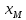 (t),
(t),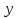 =
=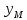 (t),
(t), 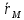 (t)=
(t)=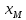 (t)
(t)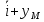 (t)
(t)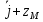 (t)
(t)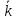
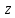 =
=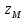 (t),
(t),Траектория – ГМ положений движущейся точки в выбранной у.н.С.О. те линия описываемая концом радиус-вектора с изменением t.