Файл: Законом О промышленной безопасности опасных производственных объектов.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 67
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
достаточно использовать некоторые числовые величины, среди которых в теории надежности наиболее употребительными являются математическое ожидание (среднее значение), мода и медиана (характеризуют положение центров группирования случайных величин на числовой оси), дисперсия, среднее квадратическое отклонение и коэффициент вариации (характеризуют рассеяние случайной величины). Значения характеристик, полученные по результатам испытаний или эксплуатации, называют статистическими оценками. Характеристики распределения используют для прогнозирования надежности.
Для дискретных случайных величин математическое ожидание Мх равно сумме произведений всех возможных значений Х на вероятности этих значений:
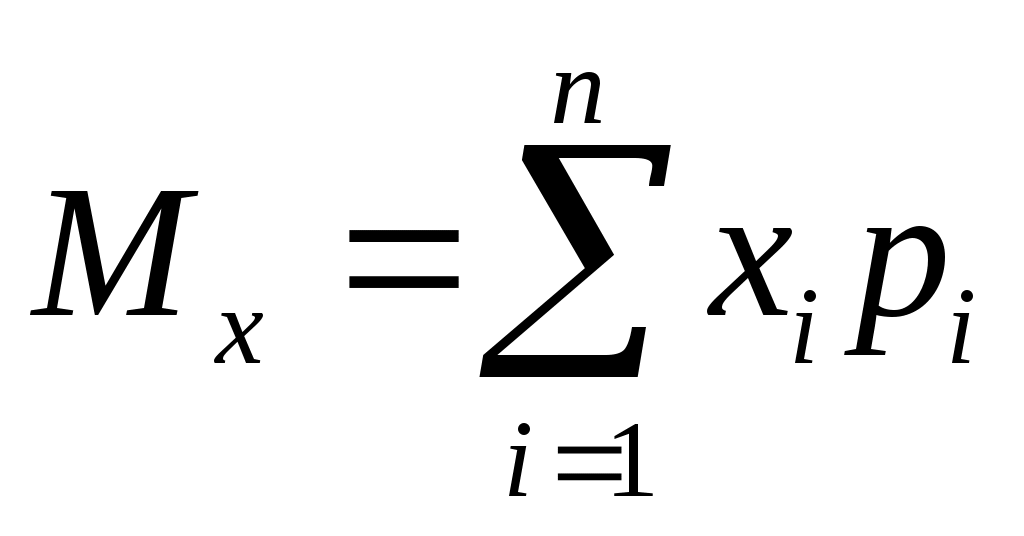
Математическое ожидание для непрерывной случайной величины выражается интегралом в бесконечных пределах от произведения непрерывно изменяющихся возможных значений случайной величины на плотность распределения
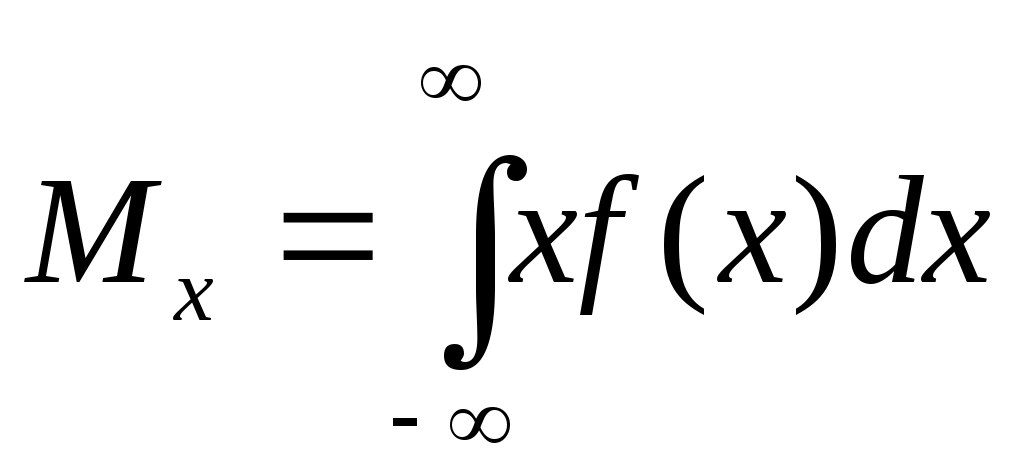
Математическое ожидание случайной величины непосредственно связано с ее средним значением. При неограниченном увеличении числа опытов среднее арифметическое значение величины х приближается к математическому ожиданию и называется оценкой среднего значения
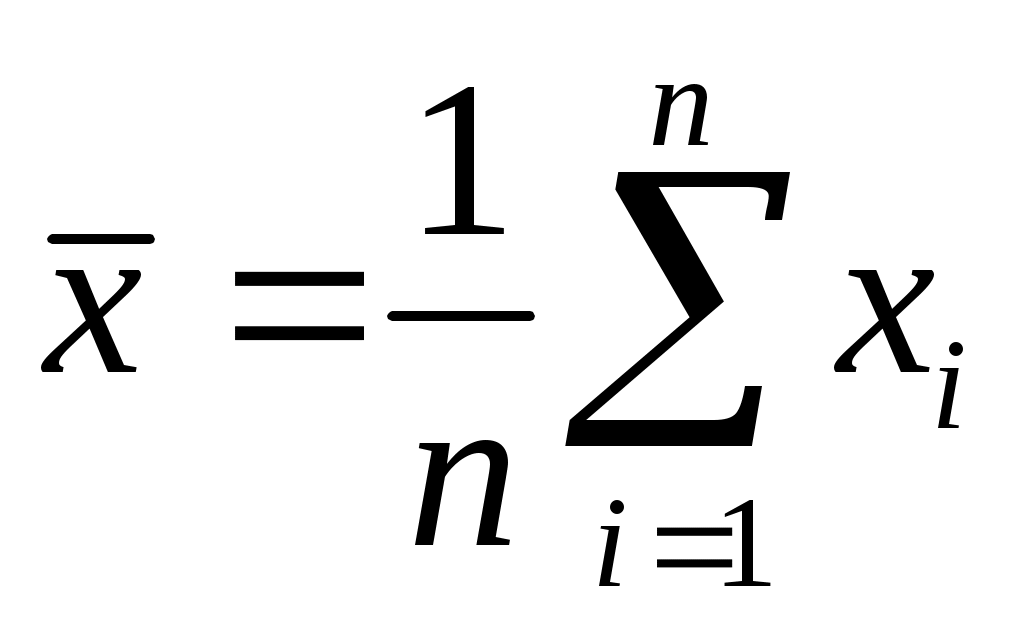
где n- общее число опытов; xi - текущее значение случайной величины.
Дисперсией (D) случайной величины называют математическое ожидание квадрата отклонения этой величины от ее математического ожидания.
Для дискретной случайной величины дисперсия равна:
Для непрерывной случайной величины дисперсия определяется из выражения
Оценка дисперсии случайной величины:
Дисперсия случайной величины является характеристикой рассеяния — разбросанности значений случайной величины около ее математического ожидания. Размерность дисперсии соответствует квадрату размерности случайной величины. Для на
глядности в качестве характеристики рассеяния удобнее использовать величину, размерность которой совпадает с размерностью случайной величины. Такой характеристикой может быть среднее квадратическое отклонение ох>которое определяется как корень квадратный из дисперсии:
Для оценки рассеяния с помощью безразмерной величины используют коэффициент вариации, который равен:
Модой случайной величины называют ее наиболее вероятное значение или то ее значение, при котором плотность вероятности максимальна.
Медиана характеризует расположение центра группирования случайной величины. Площадь под графиком функции плотности распределения делится медианой пополам.
Квантиль — значение случайной величины, соответствующее заданной вероятности. Квантиль, соответствующую вероятности 0,5, называют медианой.
Аналогично предыдущим характеристикам понятия моды и медианы даны в статистической трактовке. Для симметричного модального (т.е. имеющего один максимум) распределения математическое ожидание, мода и медиана совпадают.
Пример 3.1. Функция распределения непрерывной случайной величины Xзадана выражением
Найти коэффициент а и плотность распределения j(x).
Решение. Так как функция распределения случайной величины Xнепрерывна, то при х= 1, ах? = 1, откуда а = 1.









Механическая энергия в системе может возникнуть и как следствие тех затрат энергии, которые имели место при изготовлении отдельных частей системы и сохрани-лись в них в потенциальной форме. Например, деформация частей при перераспределе-нии внутренних напряжений, изменение объема детали после ее термической обработ-ки происходят без всяких внешних воздействий.
Тепловая энергия действует на систему и ее части при колебаниях температуры окружающей среды, при осуществлении рабочего процесса (особенно сильные тепло-вые воздействия имеют место при работе двигателей и ряда технологических машин), при работе приводных механизмов, электротехнических и гидравлических устройств.
Химическая энергия также оказывает влияние на работу системы. Даже воздух, который содержит влагу и агрессивные составляющие, может вызвать коррозию от-дельных узлов системы.
Если же оборудование системы работает в условиях агрессивных сред (обо-рудование химической промышленности, суда, многие машины текстильной промыш-ленности и др.), то химические воздействия вызывают процессы, приводящие к разру-шению отдельных элементов и узлов системы.
Ядерная (атомная) энергия, выделяющаяся в процессе превращения атомных ядер, может воздействовать на материалы (особенно в космосе), изменяя их свойства.
Электромагнитная энергия в виде радиоволн (электромагнитных колебаний) пронизывает все пространство вокруг объекта и может оказать влияние на работу элек-тронной аппаратуры.
Биологические факторы также могут влиять на работоспособность системы. Например, в тропических странах имеются микроорганизмы, которые не только разру-шают некоторые виды пластмасс, но даже могут воздействовать на металл.
Таким образом, все виды энергии действуют на техническую систему и ее меха-низмы, вызывают в ней целый ряд нежелательных процессов, создают условия для ухудшения ее технических характеристик.
4.2. Процессы, снижающие работоспособность системы
Различные виды энергии, действуя на систему, вызывают в ее узлах и деталях процессы, снижающие начальные параметры изделия. Эти процессы связаны, как пра-вило, со сложными физико-химическими явлениями и приводят к деформации, износу, поломке, коррозии и другим видам повреждений. Это, в свою очередь, влечет за собой изменение выходных параметров изделия, что может привести к отказу.
Приведем примеры данных взаимосвязей. Механическая энергия, действующая в звеньях металлорежущего станка, приводит к возникновению процесса износа его звеньев. Это вызывает искажение начальной формы сопряжении (т. е. их повреждение), что приводит к потере станком точности, которая является основным выходным пара-метром станка. При достижении определенной погрешности обработки возникает от-каз.
Химическая энергия вызывает процессы коррозии в резервуарах и трубопрово-дах агрегатов химической промышленности. Повреждение стенок резервуаров может привести вначале к ухудшению выходных параметров агрегата (загрязнение химиче-ских веществ, изменение пропускных сечений трубопроводов), а затем при разрушении стенок к полному выходу из строя изделия.
21
Сочетание механических воздействий в том числе высокочастотных колебаний, а также влияние температурных и химических факторов на элементы конструкции са-молетов приводит к тому, что в них могут возникнуть усталостные разрушения (тре-щины). Они снижают несущую способность системы, что при определенной величине повреждения приводит к разрушению элемента конструкции и может закончиться ав-рией.
Процесс, возникающий в результате действия того или иного вида энергии, мо-жет не сразу привести к повреждению изделия. Часто существует период «накопления воздействий» прежде чем начнется период внешнего проявления процесса, т. е. повре-ждение изделия. Например, для начала развития усталостной трещины необходимо оп-ределенное число циклов переменных напряжений.
Повреждение материала изделия — это отклонение его контролируемых свойств от начальных, оно связано с выходными параметрами изделия определенной зависимостью. Не всякое повреждение влияет на выходные параметры изделия. Также и определенная степень этого повреждения может не повлиять на показатели работо-способности.
В надежности машин часто пользуются понятием дефекта, т. е. такого состоя-ния изделия, при котором оно не соответствует хотя бы одному из требований техниче-ской документации, однако остается работоспособным. При этом дефект рассматрива-ется как возможная причина отказа. Понятие дефекта следует относить только к ре-зультату технологического процесса, а понятие повреждения - к результату воздейст-вий на систему при ее эксплуатации. При этом необходимо рассматривать не только факт возникновения повреждений, но и оценить степень этого повреждения. При до-стижении некоторого максимального значения степени повреждения наступает отказ изделия.
4.3. Физика отказов
4.3.1. Анализ закономерностей изменения свойств материалов
Изменение начальных свойств и состояния материалов, из которых выполнено изделие, является первопричиной потери им работоспособности, так как эти изменения могут привести к повреждению изделия и к опасности возникновения отказа.
Чем глубже изучены закономерности, описывающие процессы изменения свойств и состояния материалов, тем достовернее можно предсказать поведение изде-лия в данных условиях эксплуатации и обеспечить сохранение показателей надежности в требуемых пределах.
Хотя для оценки надежности, как правило, используются вероятностные харак-теристики, это не значит, что суждение о поведении изделия можно сделать лишь на основании статистических исследований.
Наоборот, в основе потери машиной работоспособности всегда лежат физиче-ские закономерности, но в силу разнообразия и переменности действующих факторов эти зависимости приобретают вероятностный характер.
Пусть скорость некоторого процесса повреждения материала γ есть функция ря-да входных параметров Z1, Z2,…, Znи времени t, причем данная зависимость получена на основе физико-химических законов:
22
γ = dU/dt = ϕ (Z1, Z2,…, Zn, t) (4.1)
Параметры Ziхарактеризуют условия эксплуатации (нагрузки, скорости, темпе-ратура и др.), состояние материала (твердость, прочность, качество поверхности и т. д.) и другие факторы, влияющие на протекание процесса повреждения материала. Однако при наличии только функциональной зависимости, достаточно достоверно описываю-щей данное явление, нельзя еще точно предсказать, как будет протекать данный про-цесс, так как сами аргументы Z1,… Znявляются случайными величинами.
Действительно, при работе машины происходят непредвиденные изменения и колебания нагрузок, скоростей, температур, степени загрязнения поверхностей. Более того, сами детали машины могут быть выполнены с различными допусками на техно-логические параметры (точность, однородность материала и др.).
Для дискретных случайных величин математическое ожидание Мх равно сумме произведений всех возможных значений Х на вероятности этих значений:
Математическое ожидание для непрерывной случайной величины выражается интегралом в бесконечных пределах от произведения непрерывно изменяющихся возможных значений случайной величины на плотность распределения
Математическое ожидание случайной величины непосредственно связано с ее средним значением. При неограниченном увеличении числа опытов среднее арифметическое значение величины х приближается к математическому ожиданию и называется оценкой среднего значения
где n- общее число опытов; xi - текущее значение случайной величины.
Дисперсией (D) случайной величины называют математическое ожидание квадрата отклонения этой величины от ее математического ожидания.
Для дискретной случайной величины дисперсия равна:
Для непрерывной случайной величины дисперсия определяется из выражения
Оценка дисперсии случайной величины:
Дисперсия случайной величины является характеристикой рассеяния — разбросанности значений случайной величины около ее математического ожидания. Размерность дисперсии соответствует квадрату размерности случайной величины. Для на
глядности в качестве характеристики рассеяния удобнее использовать величину, размерность которой совпадает с размерностью случайной величины. Такой характеристикой может быть среднее квадратическое отклонение ох>которое определяется как корень квадратный из дисперсии:
Для оценки рассеяния с помощью безразмерной величины используют коэффициент вариации, который равен:
Модой случайной величины называют ее наиболее вероятное значение или то ее значение, при котором плотность вероятности максимальна.
Медиана характеризует расположение центра группирования случайной величины. Площадь под графиком функции плотности распределения делится медианой пополам.
Квантиль — значение случайной величины, соответствующее заданной вероятности. Квантиль, соответствующую вероятности 0,5, называют медианой.
Аналогично предыдущим характеристикам понятия моды и медианы даны в статистической трактовке. Для симметричного модального (т.е. имеющего один максимум) распределения математическое ожидание, мода и медиана совпадают.
Пример 3.1. Функция распределения непрерывной случайной величины Xзадана выражением
Найти коэффициент а и плотность распределения j(x).
Решение. Так как функция распределения случайной величины Xнепрерывна, то при х= 1, ах? = 1, откуда а = 1.









Механическая энергия в системе может возникнуть и как следствие тех затрат энергии, которые имели место при изготовлении отдельных частей системы и сохрани-лись в них в потенциальной форме. Например, деформация частей при перераспределе-нии внутренних напряжений, изменение объема детали после ее термической обработ-ки происходят без всяких внешних воздействий.
Тепловая энергия действует на систему и ее части при колебаниях температуры окружающей среды, при осуществлении рабочего процесса (особенно сильные тепло-вые воздействия имеют место при работе двигателей и ряда технологических машин), при работе приводных механизмов, электротехнических и гидравлических устройств.
Химическая энергия также оказывает влияние на работу системы. Даже воздух, который содержит влагу и агрессивные составляющие, может вызвать коррозию от-дельных узлов системы.
Если же оборудование системы работает в условиях агрессивных сред (обо-рудование химической промышленности, суда, многие машины текстильной промыш-ленности и др.), то химические воздействия вызывают процессы, приводящие к разру-шению отдельных элементов и узлов системы.
Ядерная (атомная) энергия, выделяющаяся в процессе превращения атомных ядер, может воздействовать на материалы (особенно в космосе), изменяя их свойства.
Электромагнитная энергия в виде радиоволн (электромагнитных колебаний) пронизывает все пространство вокруг объекта и может оказать влияние на работу элек-тронной аппаратуры.
Биологические факторы также могут влиять на работоспособность системы. Например, в тропических странах имеются микроорганизмы, которые не только разру-шают некоторые виды пластмасс, но даже могут воздействовать на металл.
Таким образом, все виды энергии действуют на техническую систему и ее меха-низмы, вызывают в ней целый ряд нежелательных процессов, создают условия для ухудшения ее технических характеристик.
4.2. Процессы, снижающие работоспособность системы
Различные виды энергии, действуя на систему, вызывают в ее узлах и деталях процессы, снижающие начальные параметры изделия. Эти процессы связаны, как пра-вило, со сложными физико-химическими явлениями и приводят к деформации, износу, поломке, коррозии и другим видам повреждений. Это, в свою очередь, влечет за собой изменение выходных параметров изделия, что может привести к отказу.
Приведем примеры данных взаимосвязей. Механическая энергия, действующая в звеньях металлорежущего станка, приводит к возникновению процесса износа его звеньев. Это вызывает искажение начальной формы сопряжении (т. е. их повреждение), что приводит к потере станком точности, которая является основным выходным пара-метром станка. При достижении определенной погрешности обработки возникает от-каз.
Химическая энергия вызывает процессы коррозии в резервуарах и трубопрово-дах агрегатов химической промышленности. Повреждение стенок резервуаров может привести вначале к ухудшению выходных параметров агрегата (загрязнение химиче-ских веществ, изменение пропускных сечений трубопроводов), а затем при разрушении стенок к полному выходу из строя изделия.
21
Сочетание механических воздействий в том числе высокочастотных колебаний, а также влияние температурных и химических факторов на элементы конструкции са-молетов приводит к тому, что в них могут возникнуть усталостные разрушения (тре-щины). Они снижают несущую способность системы, что при определенной величине повреждения приводит к разрушению элемента конструкции и может закончиться ав-рией.
Процесс, возникающий в результате действия того или иного вида энергии, мо-жет не сразу привести к повреждению изделия. Часто существует период «накопления воздействий» прежде чем начнется период внешнего проявления процесса, т. е. повре-ждение изделия. Например, для начала развития усталостной трещины необходимо оп-ределенное число циклов переменных напряжений.
Повреждение материала изделия — это отклонение его контролируемых свойств от начальных, оно связано с выходными параметрами изделия определенной зависимостью. Не всякое повреждение влияет на выходные параметры изделия. Также и определенная степень этого повреждения может не повлиять на показатели работо-способности.
В надежности машин часто пользуются понятием дефекта, т. е. такого состоя-ния изделия, при котором оно не соответствует хотя бы одному из требований техниче-ской документации, однако остается работоспособным. При этом дефект рассматрива-ется как возможная причина отказа. Понятие дефекта следует относить только к ре-зультату технологического процесса, а понятие повреждения - к результату воздейст-вий на систему при ее эксплуатации. При этом необходимо рассматривать не только факт возникновения повреждений, но и оценить степень этого повреждения. При до-стижении некоторого максимального значения степени повреждения наступает отказ изделия.
4.3. Физика отказов
4.3.1. Анализ закономерностей изменения свойств материалов
Изменение начальных свойств и состояния материалов, из которых выполнено изделие, является первопричиной потери им работоспособности, так как эти изменения могут привести к повреждению изделия и к опасности возникновения отказа.
Чем глубже изучены закономерности, описывающие процессы изменения свойств и состояния материалов, тем достовернее можно предсказать поведение изде-лия в данных условиях эксплуатации и обеспечить сохранение показателей надежности в требуемых пределах.
Хотя для оценки надежности, как правило, используются вероятностные харак-теристики, это не значит, что суждение о поведении изделия можно сделать лишь на основании статистических исследований.
Наоборот, в основе потери машиной работоспособности всегда лежат физиче-ские закономерности, но в силу разнообразия и переменности действующих факторов эти зависимости приобретают вероятностный характер.
Пусть скорость некоторого процесса повреждения материала γ есть функция ря-да входных параметров Z1, Z2,…, Znи времени t, причем данная зависимость получена на основе физико-химических законов:
22
γ = dU/dt = ϕ (Z1, Z2,…, Zn, t) (4.1)
Параметры Ziхарактеризуют условия эксплуатации (нагрузки, скорости, темпе-ратура и др.), состояние материала (твердость, прочность, качество поверхности и т. д.) и другие факторы, влияющие на протекание процесса повреждения материала. Однако при наличии только функциональной зависимости, достаточно достоверно описываю-щей данное явление, нельзя еще точно предсказать, как будет протекать данный про-цесс, так как сами аргументы Z1,… Znявляются случайными величинами.
Действительно, при работе машины происходят непредвиденные изменения и колебания нагрузок, скоростей, температур, степени загрязнения поверхностей. Более того, сами детали машины могут быть выполнены с различными допусками на техно-логические параметры (точность, однородность материала и др.).