МИНОБРНАУКИ РОССИИ федеральное государственное бюджетное образовательное учреждение высшего образования «Балтийский государственный технический университет «ВОЕНМЕХ» им. Д.Ф. Устинова» (БГТУ «ВОЕНМЕХ» им. Д.Ф. Устинова»)
Факультет		А		Ракетно-космической техники
		шифр		наименование
Кафедра		А5		Динамика и управление полетом летательных аппаратов
		шифр		наименование
Дисциплина		Динамика движения ЛА

Лабораторная работа №1

Расчет траектории неуправляемых реактивных

ЛА малой дальности

Выполнил студент группы								А192
Росликов А. М.
Фамилия И.О.						подпись
Преподаватель
Лемешонок Т.Ю.
Фамилия И.О.						подпись
Оценка
«		»							2022

---

Санкт-Петербург

Цель работы: провести расчет траектории движения неуправляемого реактивного ЛА малой дальности.

Постановка задачи

В данной работе производится расчет траектории движения неуправляемого реактивного ЛА малой дальности, стартующего с направляющих. Расчет траектории разбивается на следующие этапы:

Расчет движения по направляющим

Расчет активного участка траектории движения ЛА

Расчет пассивного участка траектории движения ЛА

Для двух последних участков приходится решать системы обыкновенных дифференциальных уравнений. Для этого используются метод Эйлера 1-го порядка и метод Рунге-Кутта 4-го порядка. В ходе работы необходимо также сравнить данные методы при различных шагах интегрирования и выбрать оптимальный метод и оптимальный шаг.

В конце расчета необходимо построить таблицу зависимостей параметров ЛА 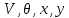от времени при выбранном методе и шаге интегрирования, а также графики 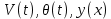для двух методов интегрирования.

Теоретическая часть

Расчет движения ЛА по направляющим:

При расчете движения по направляющим принимается во внимание действие на ЛА следующих сил: 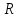– тяга, – вес ЛА, 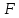– реакция направляющих, состоящая из сил трения 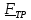и нормальной составляющей 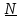. Аэродинамическими силами, ввиду малой скорости ЛА, не учитываются. Время схода и скорость схода с направляющих находятся по формулам: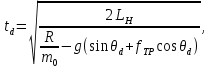





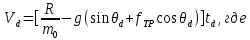
– длина направляющих, – полная масса ЛА,

---

– угол подъема направляющих, 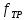– коэффициент трения скольжения, 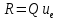( 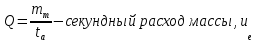– эффективная скорость истечения).

Схема сил, действующих на ЛА при движении по направляющим, представлена на рис. 1



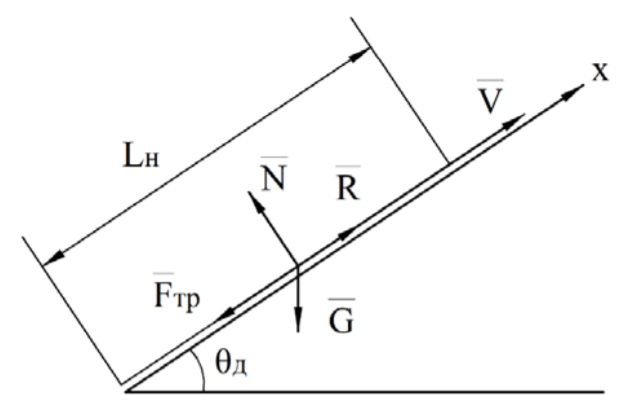
Рис. 1
Расчет активного участка траектории ЛА:

При расчете активного участка принимаются допущения: поле силы тяжести постоянно параллельно, тяга постоянна и не зависит от высоты полета, угол атаки равен нулю, а значит и подъемная сила равна нулю. Плотность воздуха есть функция от высоты и находится по формуле^



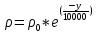
Сила лобового сопротивления рассчитывается по формуле:

,

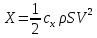причем коэффициент лобового сопротивления зависит от числа Маха M 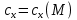. Для удобства счета полагают 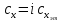, где 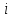– коэффициент формы, а 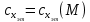– коэффициент лобового сопротивления эталонного ЛА, получаемый из таблицы для закона Сиаччи.

При данных допущениях для нахождения параметров движения приходится решать систему из следующих уравнений:









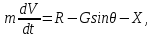
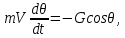
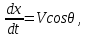
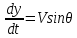
Начальными условиями являются конечные значения расчета схода ЛА с направляющей: .

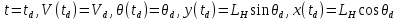Расчет пассивного участка траектории ЛА:

При расчете пассивного участка полагается , .

---

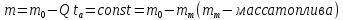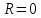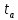
– время активного участка.

Для нахождения параметров движения приходится решать систему из следующих уравнений:









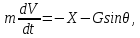
Начальными условиями являются данные о параметрах траектории в конце активного участка: .

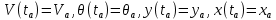Для решения систем дифференциальных уравнений используются метод Эйлера 1-го порядка и метод Рунге-Кутта 4-го порядка.


Метод Эйлера:

Основан на аппроксимации кривой прямой линией.

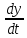=f(x,y)

НУ: t₀ ,y₀ ; h-шаг

Движемся от точки 0 к точке 1:

t₁=t₀+h

y₁=y₀+∆y, ∆y=h*tgα

По геометрическому смыслу производной tgα=f ’_t → tgα= f(t₀,y₀) → y₁=y₀+h*f(t₀,y₀)

При дальнейшем движении:

t_i=t_i-1+h

y_i=y_i-1+h*f(t_i-1,y_i-1)

и т.д.



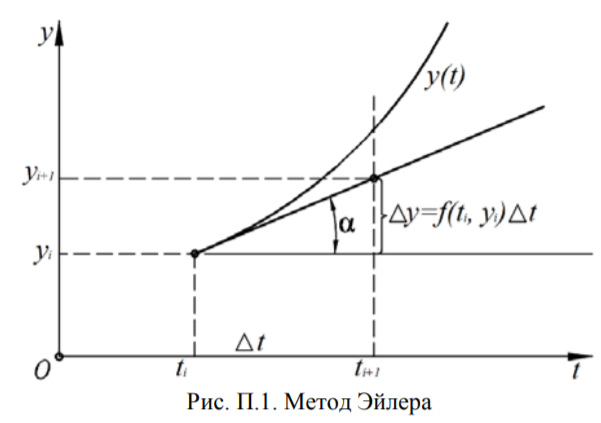
Рис. 1. Геометрическая интерпретация метода Эйлера
Метод Рунге-Кутта 4-ого порядка:

Основан на аппроксимации кривой параболой, построенной по 3 точкам.


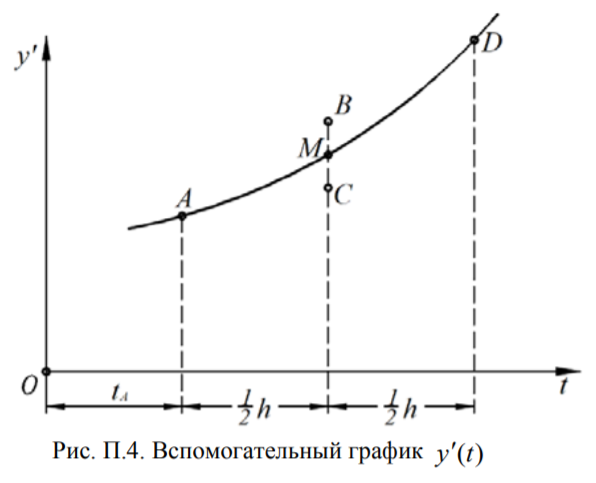
Рис. 2. Геометрическая интерпретация метода Рунге-Кутта 4-го порядка
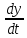=f(t,y)

НУ: t_А ,y_А; y’_A= f(t_А,y_А); h-шаг

Делим шаг пополам, получаем точку В с координатами:

t_В=t_А+ ; y_В=y_А+ *f(t_А,y_А)

Берем производную в точке В и проводим полученную под новым углом прямую из точки А → получим точку С

---

:

t_С=t_А+ ; y_С=y_А+ *f(t_В,y_В)

Берем производную в точке С и проводим полученную под новым углом прямую из точки А→ точка D:

t_D=t_А+h; y_D=y_А+h*f(t_C,y_C)

y’_M =0,5(y’_B +y’_C)

По точкам А, М, D строим параболу

Итоговые уравнения:

t_D=t_А+h; y_D=y_А+ *(y’_A +2y’_B+2y’_C +y’_D)

Метод точный, но требует вычисления производных.


Исходные данные

Для варианта 9 принимаются следующие исходные данные:

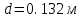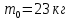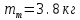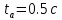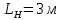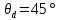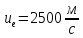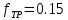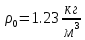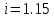Ход расчета

Расчет параметров движения на этапе схода с направляющих.

Тяга двигателя
;
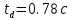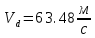
Расчет параметров на активном и пассивном участках.

Решая системы дифференциальных уравнений методом Эйлера и Рунге-Кутта при различном шаге интегрирования, получаем следующую зависимость полученной дальности полета от выбранного шага интегрирования (Таблица 1):
Таблица 1

Шаг интегрирования	Дальность, м
	Метод Эйлера	Метод Рунге-Кутта
0.1	7128.7	7156.6
0.05	6809.3	6816.9
0.01	6596.2	6597.5
0.001	6557.1	6557.4

---

Смотрите также файлы

• И в квалифицированном справочнике, и в профстандарте, то образовательная организация вправе продолжить применять квалифицированный справочник.docx

• Как сэкономить электричество.docx

• Голландская живопись как вид искусства.docx

• Конкурс Лучшие педагогические практики по формированию объективной внутренней системы оценки качества образования.docx

• Практическая работа 2 Основные средства предприятия Задача 1.docx