ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 100
Скачиваний: 10
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Составим таблицу результатов моделирования, содержащую зависимость параметров ЛА от времени (первые 10 шагов и последние 10 шагов), для метода Рунге-Кутта и шага 0.01 (Таблица 2):
Таблица 2
| | | Скорость 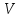 , м/с , м/с | Угол возвышения 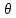 , рад. , рад. | Высота 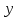 , м , м | Дальность 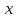 , м , м | |
| | Первые 10 шагов | |||||
| | | 0 | 0.7854 | 0 | 0 | |
| | | 70.0618 | 0,7853 | 2.1213 | 2.1217 | |
| | | 70.9048 | 0,7852 | 2.1708 | 2.1708 | |
| | | 71.7475 | 0,7851 | 2.2209 | 2.2210 | |
| | | 72.5907 | 0,7850 | 2.2717 | 2.2717 | |
| | | 73.4343 | 0,7849 | 2.3230 | 2.3230 | |
| | | 74.2782 | 0,7848 | 2.3749 | 2.3750 | |
| | | 75.1223 | 0,7847 | 2.4274 | 2.4276 | |
| | | 75.9667 | 0,7746 | 2.4805 | 2.4807 | |
| | | 76.8113 | 0,7745 | 2.5342 | 2.5344 | |
| | | | Последние 10 шагов | |||
| | 201.701 | -1.0729 | 1.6156 | 6556.1 | ||
| 201.7043 | -1.0729 | 1.4402 | 6556.2 | |||
| 201.7074 | -1.0730 | 1.2649 | 6556.3 | |||
| 201.7104 | -1.0730 | 1.0895 | 6556.4 | |||
| 201.7134 | -1.0730 | 0.9142 | 6556.5 | |||
| 201.7164 | -1.0730 | 0.7388 | 6556.6 | |||
| 201.7195 | -1.0731 | 0.5634 | 6556.7 | |||
| 201.7227 | -1.0731 | 0.3880 | 6556.8 | |||
| 201.7325 | -1.0731 | 0.2127 | 6556.9 | |||
| 201.7375 | -1.0731 | 0.0373 | 6557.0 | |||
Построение графиков зависимостей
 для двух методов интегрирования
для двух методов интегрирования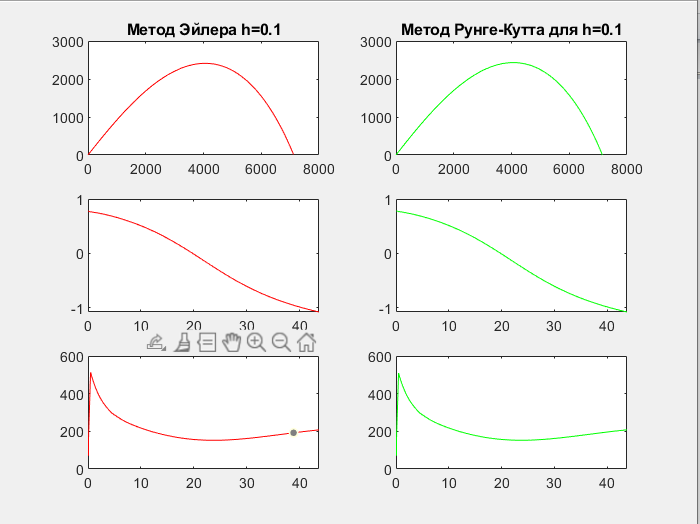
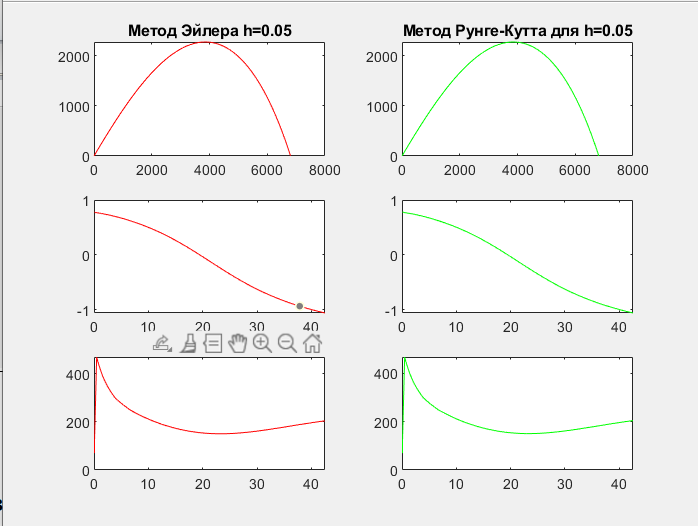
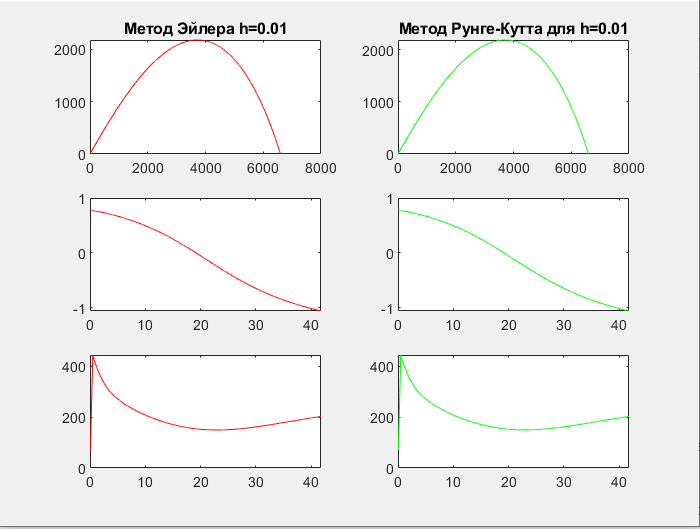
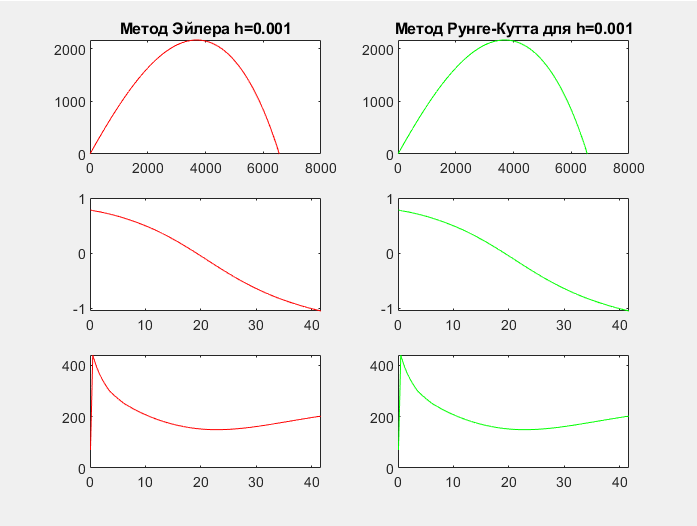
Вывод
В ходе работы был произведен расчет траектории движения неуправляемого реактивного ЛА малой дальности.
Также было произведено сравнение метода Эйлера и метода Рунге-Кутта 4-порядка. При малом шаге метод Эйлера и метод Рунге-Кутта дают практически идеальные результаты, при том, что метод Рунге-Кутта имеет более высокий параметр точности.
Приложение
clear all
clc
% ввод начальных данных
d=0.132;
m0=23;
mt=3.8;
ta=0.5;
L=3;
ue=2500;
% Рассчитать время схода с направляющих и скорость
R=(mt*ue)/ta;
td=sqrt(2*L/(R/m0-9.81*(sin(pi/4)+0.15*cos(pi/4))));
fprintf('td=%d\n',td)
Vd(9,1)=(R/m0-9.81*(sin(pi/4)+0.15*cos(pi/4)))*td;
fprintf('Vd=%d\n',Vd(9,1))
t(1)=0.1;
t(2)=0.05;
t(3)=0.01;
t(4)=0.001;
c(100)=0.225;
c(150)=0.257;
c(200)=0.26;
c(250)=0.268;
c(260)=0.274;
c(270)=0.28;
c(280)=0.295;
c(290)=0.321;
c(300)=0.361;
c(310)=0.411;
c(320)=0.46;
c(330)=0.5;
c(340)=0.542;
c(350)=0.574;
c(360)=0.603;
c(370)=0.628;
c(380)=0.648;
c(390)=0.665;
c(400)=0.68;
c(410)=0.69;
c(420)=0.7;
c(430)=0.709;
c(440)=0.715;
c(450)=0.719;
c(500)=0.735;
c(550)=0.732;
c(600)=0.721;
c(650)=0.704;
c(700)=0.68;
c(750)=0.665;
c(800)=0.645;
c(850)=0.624;
c(900)=0.605;
c(950)=0.583;
c(1000)=0.567;
H=1;
% метода Эйлера
for n=1:4
T(1)=td;
b=1;
O(9,b)=pi/4;
yt(9,b)=L*sin(O(9,b));
xt(9,b)=L*cos(O(9,b));
G=5;
% активный участок
for i=td:t(n):ta
O(9,b+1)=O(9,b)-t(n)*9.81*cos(O(9,b))/Vd(9,b);
xt(9,b+1)=xt(9,b)+t(n)*Vd(9,b)*cos(O(9,b));
yt(9,b+1)=yt(9,b)+t(n)*Vd(9,b)*sin(O(9,b));
m=m0-mt*i/ta;
g=0;
k=1;
while k>=0
if Vd(9,b)<=350||Vd(9,b)>=450
g=g+50;
k=Vd(9,b)-g;
else
g=g+10;
k=Vd(9,b)-g;
end
end
Vd(9,b+1)=Vd(9,b)+t(n)*(R/m-9.81*sin(O(9,b))-(1.23*exp(-yt(9,b)/10000)*pi*d^2/4*(Vd(9,b))^2*1.15*c(g))/(2*m));
T(b+1)=i;
X(b)=xt(9,b);
Y(b)=yt(9,b);
O2(b)=O(9,b);
V(b)=Vd(9,b);
if G>0 % счетчик для начальных значений активного участка
U1(H,6-G)=roundn(Vd(9,b), -4);
U2(H,6-G)=roundn(O(9,b), -4);
U3(H,6-G)=roundn(xt(9,b), -4);
U4(H,6-G)=roundn(yt(9,b), -4);
G=G-1;
end
b=b+1;
end
for N= 1:5 % счетчик для конечных значений активного участка
U1(H+1,N)=roundn(Vd(9,b-5+N), -4);
U2(H+1,N)=roundn(O(9,b-5+N), -4);
U3(H+1,N)=roundn(xt(9,b-5+N), -4);
U4(H+1,N)=roundn(yt(9,b-5+N), -4);
end
G=5;
%Рассчет пассивного участка
while yt(9,b)>=0
O(9,b+1)=O(9,b)-t(n)*9.81*cos(O(9,b))/Vd(9,b);
xt(9,b+1)=xt(9,b)+t(n)*Vd(9,b)*cos(O(9,b));
yt(9,b+1)=yt(9,b)+t(n)*Vd(9,b)*sin(O(9,b));
g=0;
k=1;
while k>0
if Vd(9,b)<=350||Vd(9,b)>=450
g=g+50;
k=Vd(9,b)-g;
else
g=g+10;
k=Vd(9,b)-g;
end
end
Vd(9,b+1)=Vd(9,b)+t(n)*(-9.81*sin(O(9,b))-(1.23*exp(-yt(9,b)/10000)*pi*d^2/4*(Vd(9,b))^2*1.15*c(g))/(2*m));
T(b)=T(b-1)+t(n);
X(b)=xt(9,b);
Y(b)=yt(9,b);
O2(b)=O(9,b);
V(b)=Vd(9,b);
if G>0 % счетчик для начальных значений пассивного участка
U1(H,12-G)=roundn(Vd(9,b), -4);
U2(H,12-G)=roundn(O(9,b), -4);
U3(H,12-G)=roundn(xt(9,b), -4);
U4(H,12-G)=roundn(yt(9,b), -4);
G=G-1;
end
b=b+1;
end
disp ("Максимумы по Эйлеру")
for N= 1:5 % счетчик для конечных значений пассивного участка
U1(H+1,N+6)=roundn(Vd(9,b-11+N), -4);
U2(H+1,N+6)=roundn(O(9,b-11+N), -4);
U3(H+1,N+6)=roundn(xt(9,b-11+N), -4);
U4(H+1,N+6)=roundn(yt(9,b-11+N), -4);
QW1 = max(max(xt));
disp (QW1)
end
H=H+2; % конец счетчика
figure(n)
subplot(3,2,1);
plot(X, Y,'r')
title( sprintf('Метод Эйлера h=%g',t(n)));
subplot(3,2,3);
plot(T, O2,'r')
subplot(3,2,5);
plot(T, V,'r')
T=0;
end
H=10;
% метод Рунге-Кутта
for n=1:4
b=1;
h=1;
O(h,b)=pi/4;
xt(h,b)=L*cos(O(h,b));
yt(h,b)=L*sin(O(h,b));
Vd(h,b)=Vd(9,1);
T(1)=td;
G=5;
% активный участок
for i=td:t(n):ta
m=m0-mt*i/ta;
for h=1:4
k=1;
if h==2||h==3
k=0.5;
end
if h>1
O(h,b)=O(1,b)+t(n)*k*O(h+3,b);
xt(h,b)=xt(1,b)+t(n)*k*xt(h+3,b);
yt(h,b)=yt(1,b)+t(n)*k*yt(h+3,b);
Vd(h,b)=Vd(1,b)+t(n)*k*Vd(h+3,b);
end
O(h+4,b)=-9.81*cos(O(h,b))/Vd(h,b);
xt(h+4,b)=Vd(h,b)*cos(O(h,b));
yt(h+4,b)=Vd(h,b)*sin(O(h,b));
g=0;
while k>0
if Vd(h,b)<=350||Vd(h,b)>=450
g=g+50;
k=Vd(h,b)-g;
else
g=g+10;
k=Vd(h,b)-g;
end
end
Vd(h+4,b)=R/m-9.81*sin(O(h,b))-(1.23*exp(-yt(h,b)/10000)*pi*d^2/4*(Vd(h,b))^2*1.15*c(g))/(2*m);
end
O(1,b+1)=O(1,b)+t(n)/6*(O(5,b)+2*(O(6,b)+O(7,b))+O(8,b));
xt(1,b+1)=xt(1,b)+t(n)/6*(xt(5,b)+2*(xt(6,b)+xt(7,b))+xt(8,b));
yt(1,b+1)=yt(1,b)+t(n)/6*(yt(5,b)+2*(yt(6,b)+yt(7,b))+yt(8,b));
Vd(1,b+1)=Vd(1,b)+t(n)/6*(Vd(5,b)+2*(Vd(6,b)+Vd(7,b))+Vd(8,b));
T(b+1)=i;
X1(b)=xt(1,b);
Y1(b)=yt(1,b);
O1(b)=O(1,b);
V1(b)=Vd(1,b);
if G>0 % счетчик для начальных значений активного участка
U1(H,6-G)=roundn(Vd(1,b), -4);
U2(H,6-G)=roundn(O(1,b), -4);
U3(H,6-G)=roundn(xt(1,b), -4);
U4(H,6-G)=roundn(yt(1,b), -4);
G=G-1;
end
b=b+1;
end
for N= 1:5 % счетчик для конечных значений активного участка
U1(H+1,N)=roundn(Vd(1,b-5+N), -4);
U2(H+1,N)=roundn(O(1,b-5+N), -4);
U3(H+1,N)=roundn(xt(1,b-5+N), -4);
U4(H+1,N)=roundn(yt(1,b-5+N), -4);
end
G=5;
%Расчет пассивного участка
while yt(1,b)>=0
for h=1:4
k=1;
if h==2||h==3
k=0.5;
end
if h>1
O(h,b)=O(1,b)+t(n)*k*O(h+3,b);
xt(h,b)=xt(1,b)+t(n)*k*xt(h+3,b);
yt(h,b)=yt(1,b)+t(n)*k*yt(h+3,b);
Vd(h,b)=Vd(1,b)+t(n)*k*Vd(h+3,b);
end
O(h+4,b)=-9.81*cos(O(h,b))/Vd(h,b);
xt(h+4,b)=Vd(h,b)*cos(O(h,b));
yt(h+4,b)=Vd(h,b)*sin(O(h,b));
g=0;
while k>0
if Vd(h,b)<=350||Vd(h,b)>=450
g=g+50;
k=Vd(h,b)-g;
else
g=g+10;
k=Vd(h,b)-g;
end
end
Vd(h+4,b)=-9.81*sin(O(h,b))-(1.23*exp(-yt(h,b)/10000)*pi*d^2/4*(Vd(h,b))^2*1.15*c(g))/(2*m);
end
O(1,b+1)=O(1,b)+t(n)/6*(O(5,b)+2*(O(6,b)+O(7,b))+O(8,b));
xt(1,b+1)=xt(1,b)+t(n)/6*(xt(5,b)+2*(xt(6,b)+xt(7,b))+xt(8,b));
yt(1,b+1)=yt(1,b)+t(n)/6*(yt(5,b)+2*(yt(6,b)+yt(7,b))+yt(8,b));
Vd(1,b+1)=Vd(1,b)+t(n)/6*(Vd(5,b)+2*(Vd(6,b)+Vd(7,b))+Vd(8,b));
T(b)=T(b-1)+t(n);
X1(b)=xt(1,b);
Y1(b)=yt(1,b);
O1(b)=O(1,b);
V1(b)=Vd(1,b);
if G>0 % счетчик для начальных значений пассивного участка
U1(H,12-G)=roundn(Vd(1,b), -4);
U2(H,12-G)=roundn(O(1,b), -4);
U3(H,12-G)=roundn(xt(1,b), -4);
U4(H,12-G)=roundn(yt(1,b), -4);
G=G-1;
end
b=b+1;
end
disp ("Максимумы по Рунге-Кутту")
for N= 1:5 % счетчик для конечных значений пассивного участка
U1(H+1,N+6)=roundn(Vd(1,b-11+N), -4);
U2(H+1,N+6)=roundn(O(1,b-11+N), -4);
U3(H+1,N+6)=roundn(xt(1,b-11+N), -4);
U4(H+1,N+6)=roundn(yt(1,b-11+N), -4);
QW2 = max(max(xt));
disp (QW2)
end
H=H+2; % конец счетчика
figure(n)
subplot(3,2,2);
plot(X1, Y1,'g')
title( sprintf('Метод Рунге-Кутта для h=%g',t(n)))
subplot(3,2,4);
plot(T, O1,'g')
subplot(3,2,6);
plot(T, V1,'g')
T=0;
end