Добавлен: 06.11.2023
Просмотров: 23
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Иркутский государственный университет путей сообщения»
(ФГБОУ ВО ИрГУПС)
Факультет «Транспортные системы»
Кафедра «Физика, механика и приборостроение»
Отчет
По лабораторной работе №8
«Напряжённое состояние в зонах контакта ролика подшипника с его кольцом, глубина рытвин контактного износа и рост трещин (живучесть конструкций) в условиях циклического нагружения»
ЛР.420300.12.04.01.2023
| Выполнил студент гр. ПСм.1-22-1 Воробьев В.Д. «___» __________ 2023 г. | Проверил кандидат технических наук, доцент, преподаватель кафедры ФМиП Зеньков Е.В. «___» __________ 2023 г. |
Иркутск, 2023 г.
Задачи:
1. Выполнить расчет коэффициента К. Расчетное значение К вычислить с помощью
‚ в котором значения d— нормальное напряжение в направлении х, и г соответствуют ближайшим к вершине трещины узлам, расположенным в плоскостисимметрии пластины.
2. Оценить погрешность расчётного и теоретического значений величины коэффициента интенсивности напряжений.
Исходные данные:
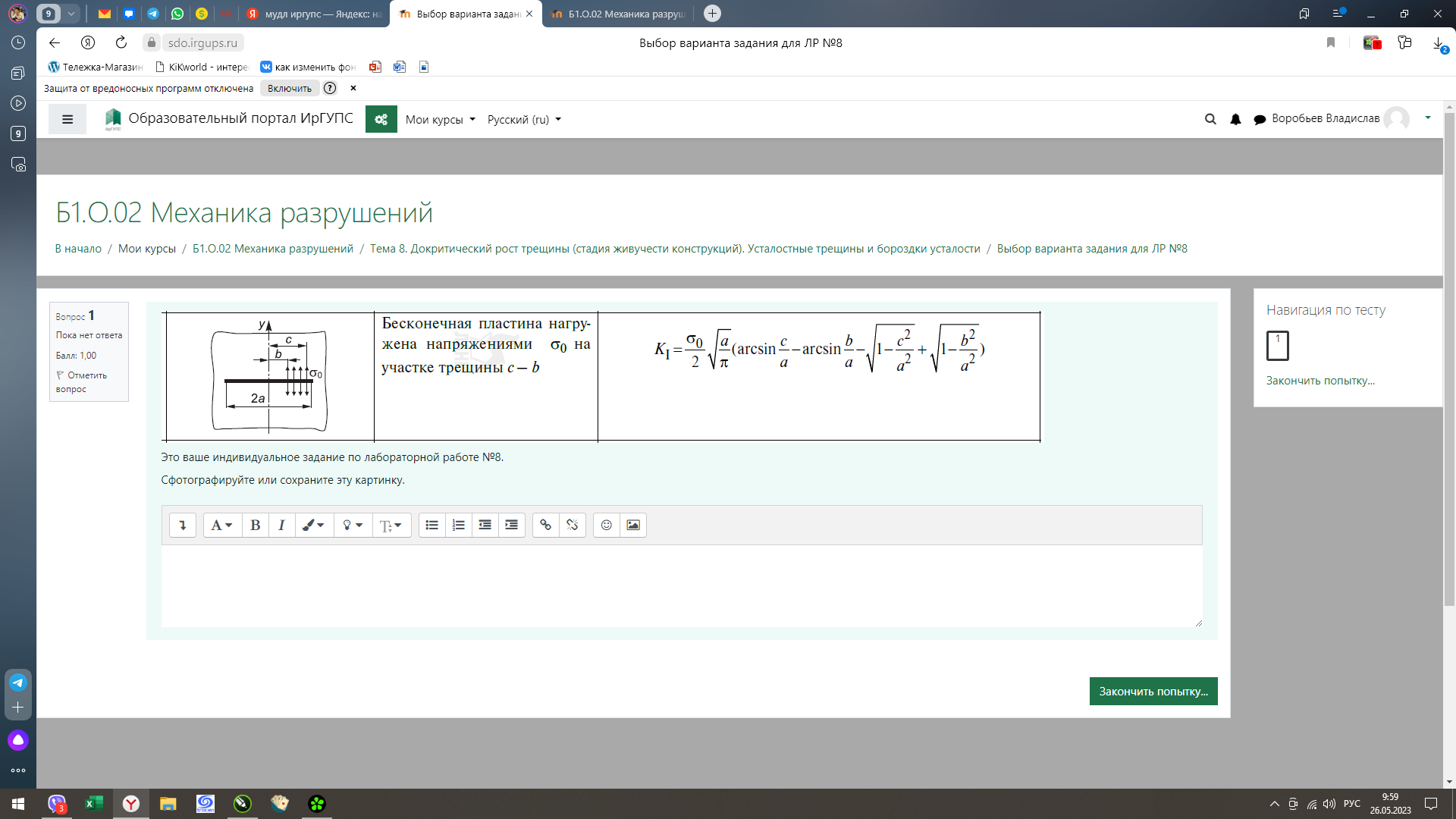
Рисунок 1 – Заданная модель плоскости с трещиной
(1)1. Расчет теоретического значений величины коэффициента интенсивности напряжений
Зададим значения параметров d0=100; Пи=3,14; с=3; а=5; b=2.
Подставим заданные параметры в формулу 1.
Получим,
| | |
| | ||
| | ||
| |
2. Расчет коэффициента К с помощью программы FEMAP
Построим плоскость размерами 100х100х0,5мм.
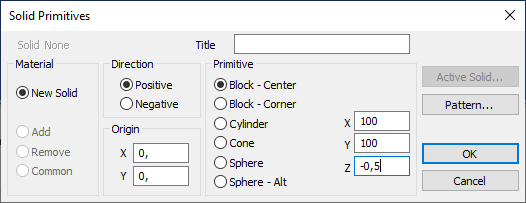
Рисунок 2 – Построение плоскости размерами 100х100х0,5мм.
Зададим трещину в плоскости, длинной в 10 раз меньше габаритов плоскости.
Рисунок 3 – Построение трещины в плоскости
Разобьём объект на конечные элементы и зададим паромеры материала
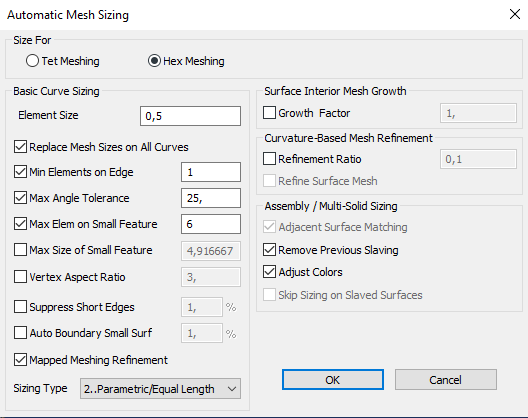
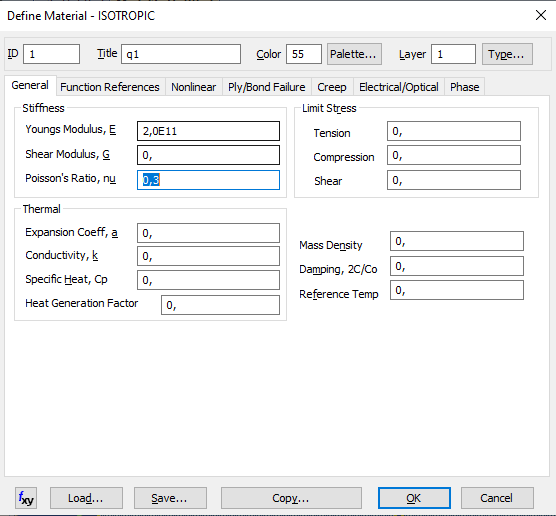
Рисунок 4 – Заданный размер КЭ, моделирование материала балки
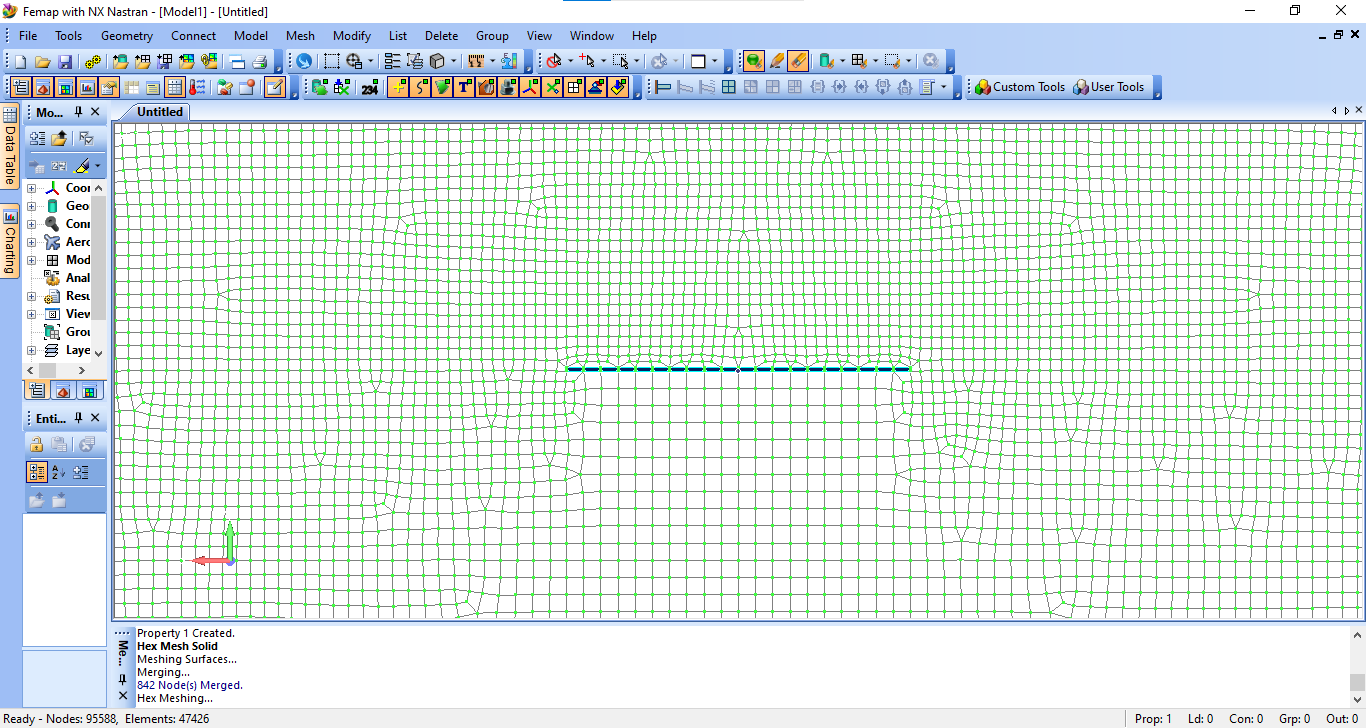
Рисунок 5 – Модель разбитая на конечные элементы
Зададим напряжение на краю трещины и закрепить края плоскости.
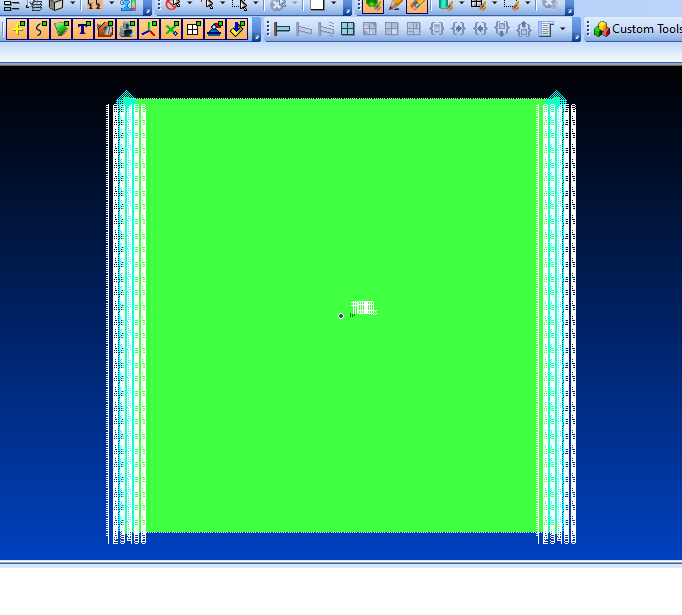
Рисунок 6 – Модель с нагружением
Замерим смоделированное напряжение в точке края трещины
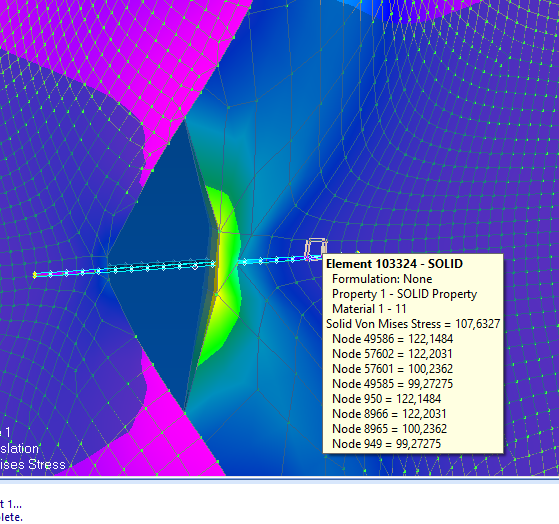
Рисунок 7 – Параметры напряжения в точке на краю трещины
3. Рассчитаем коэффициент интенсивности напряжений по полученному значению моделирования
В формулу 1 введем данные d0=107,6327; Пи=3,14; с=3; а=5; b=2.
Получим,
| | |
| | ||
| |
4. Расчет погрешности путем сравнения расчётного и теоретического значений величины коэффициента интенсивности напряжений
Обозначим К1 как коэффициент теоретического значения, К2- коэффициент расчетного значения.
(К2-К1)/К2 = (23,6668-22,9988)/(23,6668) = 0,0282
Заключение
В ходе лабораторной работы были рассчитаны теоретический и расчетный коэффициенты интенсивности напряжений. Погрешность результатов расчетов составила 2,82%