ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 31
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Метод кривых распределения
Статистический метод дает возможность не ставить специальные эксперименты, заменяя их наблюдениями непосредственно на производстве. При этом нужно лишь регламентировать условия операции и считаться с законом больших чисел, на основе которого делают выводы при всяких статистических исследованиях. Согласно этому закону при увеличении числа наблюдений над однородными явлениями частость появления какого-либо события в прошлом приближается к вероятности появления его в будущем (частостью называют отношение числа случаев m, когда событие наблюдалось, к общему числу n сделанных наблюдений; вероятность – отношение числа случаев, благоприятствующих данному событию, ко всему числу возможных случаев; вероятность достоверного события равна единице (100%), невозможного – нулю.
Вышеприведенное условие закона больших чисел означает, что не всякое измерение размеров можно положить в основу выводов о погрешностях обработки. Например, величина рассеивания V= 0,15, полученная после обработки партии из 25 деталей, является критерием погрешности обработки, достаточно достоверным для данной партии, но не больше. Эта величина будет неправильной (малодостоверной), если принять ее в качестве норматива, так как число обработанных деталей (число наблюдений) слишком мало.
Наглядное представление о действительной точности операционного размера носит кривая распределения размеров. Получившееся поле рассеивания V разделяют на некоторое число равных интервалов и в выбранном масштабе изображают на оси абсцисс. Далее подсчитывают частость
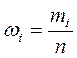,где mi – количество деталей с размером, попавшим в каждый интервал разбивки (по оси Х). Далее выбирают масштаб по оси ординат и из середины каждого интервала откладывают соответствующую частоту в виде отрезка. Соединяя концы этих отрезков, получают ломаную линию, называемую практической кривой распределения.
| | |
| |  |
Рис.3.9. Практическая кривая распределения размеров(пояснения в тексте)
Если бы количество деталей было бы безгранично велико, то естественно безграничным могло быть и число интервалов. Тогда ломаная превратилась бы в плавную кривую и изображала закон распределения размеров.
При выбранном масштабе построения форма кривой распределения зависит только от разности значений размеров. В исследованиях, связанных с определенным заданным размером, принимают за начало координат среднее значение L з ср.; таким образом достигается наибольшая наглядность (рис.3.9).
Параметры кривой. Кривую распределения характеризуют следующие главные параметры:
1. Поле рассеивания размеров. Величина его
V = Lдmax – Lдmin. (3.4)
2. Центр группирования отклонений. Положение его в поле рассеивания соответствует среднему значению действительных размеров (в случае симметричной кривой):
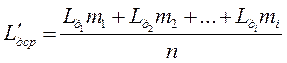, (3.5)где n –общее число измерений (деталей).
Заметим, что, не зная характера распределения, мы вынуждены считать, что
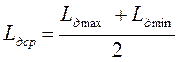, (3.6)что правильно только при совпадении центра группирования с серединой поля рассеивания, т.е. для симметричных фигур (для нашей выше приведенной кривой центр группирования сместится несколько влево).
3. Абсолютная несимметрия. Этот параметр характеризует несимметричность кривой. Величина его ε представляет собой смещение центра группирования с середины поля рассеяния
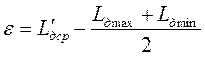. (3.7)4. Среднеквадратическое отклонение размеров от центра группирования
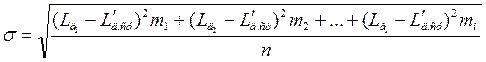. (3.8)В статистических исследованиях этот параметр играет особо важную роль.
Во-первых, величина σ правильнее, чем величина поля V, характеризует интенсивность рассеяния. Например, поле V у кривой 1 и у кривой 2 одинаково (рис. 3.10).
|
|
|
Рис. 3.10. О роли σ и V при оценке кривых распределения (пояснения в тексте)
Однако при V1 = V2 среднеквадратическое отклонение σ1< σ2; это свидетельствует о том, что в первом варианте стабильность технологии более высокая, чем во втором.
Во-вторых, параметром σ широко пользуются при переходе от практических кривых к теоретическим законам распределения и при сопоставлении законов. Практические кривые получаются в виде ломаных линий, имеющих не вполне правильную форму. Использовать их для вывода общих закономерностей затруднительно. Поэтому их заменяют подходящими «теоретическими» кривыми, изображающими вполне определенные законы, задаваемые уравнениями вида y=f(x).
В- третьих, величина σ является единственным параметром, определяющим форму так называемой кривой нормального распределения (закон Гаусса), имеющий для технологии важное значение, так как к ней достаточно близко подходят практические кривые. Уравнение этой кривой в координатах с началом в центре группирования имеет вид
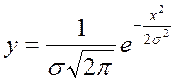, (3.9)где е – основание натуральных логарифмов (е=2,71828).
Кривая автоматически приближается к оси абсцисс. Она имеет две точки перегиба – на расстоянии + σ и – σ от центра группирования. При таком законе распределения 25% всех деталей партии находятся в интервале Х = ± 0,3σ; 50% - в интервале Х = ± 0,7σ; 75% - в интервале Х = ± 1,1σ, 99,73% - в интервале ± 3σ. В связи с этим считают, что практически все поле рассеяния находится в интервале ± 3σ (ошибка составляет лишь 0,27%), т.е. принимают
V = Lд max – Lд min = 6σ.
Влияние вида погрешности на характер распределения. Применяя метод кривых распределения к изучению погрешности обработки партии деталей, различают три «чистых» (теоретических) вида погрешностей:
а) постоянные;
б) закономерно-изменяющиеся;
в) случайные.
|
|
|
|
|
|
|
Погрешность партии деталей называют
постоянной, если погрешности деталей, входящих в партию, одинаковые. Такая погрешность получилась бы под действием фактора, неизменного во время обработки всей партии (например, установка инструмента на размер дает одну и ту же погрешность при условии, конечно, что другие факторы отсутствуют). У постоянной погрешности поле рассеяния равно нулю (см. рис. 3.11, а).
| | | | | ||
| |
| |
|
Рис. 3.11. Влияние постоянной а и закономерно-меняющейся б погрешностей на распределение размеров
Погрешность партии деталей называют закономерноизменяющейся, если по ходу обработки партии можно видеть закономерность в изменении погрешности деталей. У такой погрешности форма кривой распределения зависит от закона изменения факторов, вызывающих погрешность. На рис. 3.11, б показана типичная закономерность износа инструмента h и в соответствии с этим кривая распределения размеров.
Постоянные и закономерноизменяющиеся погрешности носят общее название систематических погрешностей.
|
|
|
|
|
|