ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 32
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Погрешность обработки партии деталей называют случайной, если в ходе обработки партии видимая закономерность изменения погрешностей деталей отсутствует. При этом ни величину, ни направление погрешности какой-либо из деталей нельзя заранее определить. Такая погрешность получилась бы под действием одного или нескольких случайных факторов, т.е. таких, которые сами изменяются случайно, или же под влиянием большого числа однородных (примерно одинаковых по влиянию) переменных факторов, хотя бы каждый из них и был не случайным. Кривая распределения случайной погрешности является кривой нормального распределения (рис. 3.12).| | |
| |  |
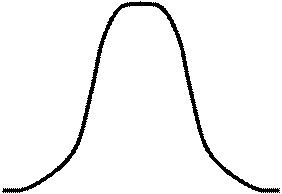Рис. 3.12. Влияние случайных погрешностей на характер распределения(пояснения в тексте)
На практике ни одна из «чистых» погрешностей партии получиться не может. Постоянная или закономерноизменяющаяся не могут получиться потому, что на действие крупного постоянного или закономерноизменяющегося фактора обязательно накладывается действие множества мелких переменных факторов (колебания величины припуска, свойств материала детали, температурных условий, условий смазки, различия во влиянии неточностей станка, приспособления, износа инструмента, различия в силе закрепления деталей и т.д.). Случайная же не может получиться в чистом виде ввиду неизбежности влияния какого-либо крупного постоянного фактора или переменного, не носящего случайный характер. Поэтому действительная погрешность обработки партии деталей всегда является более сложной.
Исходные положения для анализа кривых. При анализе руководствуются следующими основными положениями:
1. Ввиду большого числа различных производственных погрешностей, влияющих на выдерживаемый при обработке размер Lз ср, погрешность обработки партии деталей в наилучшем случае должна быть случайной величиной, подчиняющейся закону Гаусса. Это означает, что распределение погрешностей деталей, входящих в партию, должно следовать кривой нормального распределения с центрами группирования, совпадающими с Lз ср (рис. 3.12). Получив такое распределение, можно заключить, что среди производственных погрешностей не было крупных, доминировавших над остальными. Следовательно, крупные были выявлены и устранены при разработке, наладке и апробировании операции. Осталось лишь множество мелких производственных погрешностей, в отдельности малосущественных. Устранение одной из них или нескольких уже не может привести к заметному уменьшению погрешности обработки. Точностные возможности метода обработки практически оказываются исчерпанными. Существенное уменьшение погрешности обработки, если оно необходимо, требует перехода к иному методу обработки, более точному в целом, чем рассматриваемый (например, переход от точения к шлифованию, от зенкерования к развертыванию и т.п.).
При таком распределении величина поля рассеяния V = 6σ. Наибольшая из погрешностей деталей имеет величину, равную 3 σ.
2. Всякое отступление от закона нормального распределения указывают на то, что производственные погрешности, вызвавшие погрешность обработки, были неоднородные. Среди них была одна или несколько доминировавших над совокупностью остальных.
3. Влияние доминирующей постоянной производственной погрешности выражается в том, что центр группирования, оставаясь в середине поля рассеивания (ε = 0), смещается от значения Lз ср на величину μ, представляющую собой постоянную погрешность обработки (рис. 3.13). У таких деталей величина поля рассеяния V = 6 σ, но наибольшая из погрешностей деталей имеет величину, равную (3 σ + μ).
| | |
| |  |
Рис. 3.13. Влияние постоянной погрешности μ на распределение размеров(пояснения в тексте)
Погрешность μ может быть обусловлена неточностью установки инструмента на размер Lз.ср и является неизбежной. Значительная по сравнению с полем рассеяния постоянная погрешность μ указывает на несовершенство метода, которым устанавливали инструмент. Отличными считают методы, обеспечивающие μ ≤ 0,5 σ. При обработке мерным инструментом роль неточности установки инструмента на размер играет неточность диаметра инструмента.
4. Влияние доминирующей переменной производственной погрешности внешне выражается в том, что форма кривой отличается от формы кривой нормального распределения.
Новая форма зависит от закона изменения доминирующей погрешности и от того, как велика последняя по сравнению с совокупностью остальных. В зависимости от этого закона центр группирования может остаться в середине рассеяния, т.е. кривая будет симметричной (ε = 0) или же он может сместиться с середины поля, т.е. кривая будет несимметричной (ε ¹ 0).
5. Наиболее часто в роли доминирующей закономерноизменяющейся производственной погрешности выступает износ режущего инструмента, в роли доминирующей постоянной – неточность установки инструмента, вызывающая погрешность μ.
6. Доминирующая закономерноизменяющаяся производственная погрешность вызывает в ходе обработки закономерное увеличение поля рассеяния и закономерно изменяет величину постоянной погрешности μ.
Получение двухвершинной кривой, хотя партия обрабатывалась при одной установке инструмента, указывает на то, что в какой-то момент обработки в действие включился непредвиденный крупный постоянный фактор – сбилось положение инструмента, выкрошилось режущее лезвие инструмента и др.
В практике технологии машиностроения распределение размеров в подавляющем большинстве случае совпадает с распределением Гаусса. Зная это, можно существенно упростить самоисследование операций, ограничившись достаточно малым числом опытов–наблюдений. Подсчитав для обработанных деталей (50 ÷ 100 шт.) получившуюся величину σ, можно, минуя построение кривой распределения (практической кривой), сразу же определить поле рассеяния (V=6 σ).
Наряду с этим упрощается решение задач, связанных с получением ожидаемой точности:
а) задач о возможности применения данного метода обработки;
б) задач о том, какая доля допуска на заданный размер может быть использована в качестве допуска на постоянную погрешность (μ) – при установке инструмента на размер или в качестве допуска на изготовление и износ мерного инструмента.
Наиболее важное общее практическое значение исследований погрешности с помощью кривых распределения состоит в том, что они позволяют составить обоснованные нормативы точности (поле рассеяния V = 6 σ), которую можно ожидать от различных методов обработки. Именно с методом (процессом) обработки (станок, инструмент, режим) связана большая часть производственных погрешностей, аналитические исследования которых невозможны или очень трудоемки.