ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 375
Скачиваний: 11
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Семинар 1
Раздел 2. Облигации
«Решение задач по темам: Текущая стоимость облигации. Рыночная и текущая доходность. Доходность к погашению. Средний срок поступления дохода. Дюрация. Выпуклость облигации. Иммунизация портфеля облигаций. Оценивание облигаций в произвольный момент времени»
Направление: Прикладная математика и информатика Дисциплина: Финансовая математика и её приложения
Аудиторная работа Текущая стоимость облигации. Рыночная цена и текущая доходность.
1. Найти текущую стоимость облигации, если ее номинальная стоимость составляет 1500 у.е., срок до погашения 3 года, а купонные платежи выплачиваются в конце каждого года по годовой купонной ставке 15%. Банковская процентная ставка равна 11%.
Решение:
Текущую стоимость облигации определим по формуле:
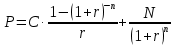
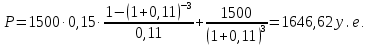
Ответ: текущая стоимость облигации будет равна 1646,62 у.е.
2. Рыночная цена облигации составляет 5200 руб., номинальная стоимость равна 4000 руб., срок до погашения – 6 лет, купонные ежегодные платежи – 900 руб., доходность – 10%. Стоит ли продать облигацию и почему?
Решение:
Текущую стоимость облигации определим по формуле:
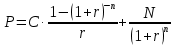
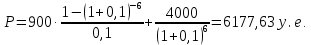
Ответ: текущая стоимость облигации больше рыночной, то такую облигации не нужно продавать, т.к. по погашению облигации в срок можно получить больше дохода.
3. Три облигации с одинаковой номинальной стоимостью 3000 руб., купонной ставкой 8% и сроком до погашения 5 лет имеют различные текущие доходности к моменту погашения – 11%, 12% и 13%. Как будут отличаться рыночные цены облигаций? Найдите их.
Решение:
Текущую стоимость облигации определим по формуле:
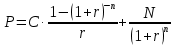
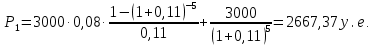
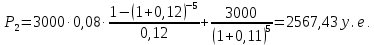
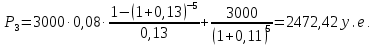
Ответ: c ростом доходности к моменту погашения рыночная цены облигации уменьшается.
4. Используя приближённую формулу, найти доходность к погашению облигации со сроком 8 лет, номинальной стоимостью 3460 и купонной ставкой 9% при розничной цене на 12% больше номинальной.
Решение:
Доходность к погашению облигации определим по формуле:
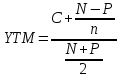
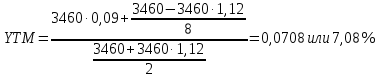
Ответ: доходность к погашению равна 7,08%
5. Найти доходность к погашению следующей облигации. Период обращения ???? = 10 лет, номинальная стоимость ???? = 1000 у.е., ежегодные купонные выплаты ???????? = 50, рыночная цена ???? = 900 у.е.
Решение:
Доходность к погашению облигации определим по формуле:
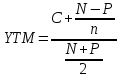
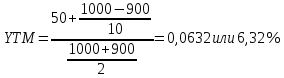
Ответ: доходность к погашению равна 6,32%
Средний срок поступления дохода. Дюрация. Выпуклость облигации. Иммунизация портфеля облигаций.
6. Купонная ставка 6-летней облигации номиналом 1000 руб. равна 14,5% годовых (выплаты в конце года). Найти средний срок поступления дохода от облигации.
Решение:
Средний срок определим по формуле:
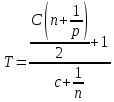
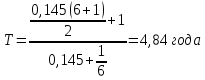
Ответ: средний срок поступления дохода от облигации составит 4,84 года
7. Купонная ставка 8-летней облигации номиналом 5000 руб. равна 15% годовых, выплаты производятся один раз в квартал. Найти средний срок поступления дохода от облигации.
Решение:
Средний срок определим по формуле:
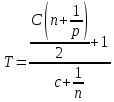
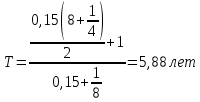
Ответ: средний срок поступления дохода от облигации составит 5,88 лет
8. Найти дюрацию потока платежей (1500;1), (2500;2), (3500;3), (4500;4) при процентной ставке ???? = 11%.
Решение:
Дюрацию определим по формуле:
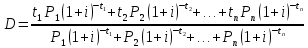
Найдем приведенную величину потока
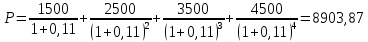
Найдем весовые коэффициенты
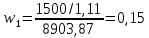
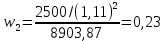
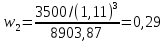
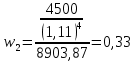
Теперь по формуле определим дюрацию потока
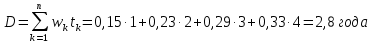
Ответ: дюрация потока составит 2,8 года.
9. Облигация продается по номинальной стоимости со сроком погашения 6 лет с выплатой купонов в конце года по купонной ставке 15,5%. Найти дюрацию облигации.
Решение:
Дюрацию облигации определим по формуле:
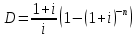
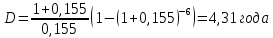
Ответ: дюрация облигации составит 4,31 года
10. Облигация со сроком погашения 11 лет и купонной ставкой 12% имеет доходность к погашению ???? = 7,5%. Найти ее дюрацию.
Решение:
Дюрацию облигации определим по формуле:
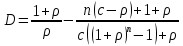
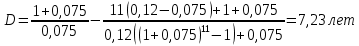
Ответ: дюрация облигации равна 7,23 лет.
11. Дюрация облигации равна 10. Известно, что ее доходность к погашению увеличилась с 12,5% до 13%. На сколько процентов изменилась цена облигации.
Решение:
Воспользуемся формулой:
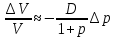
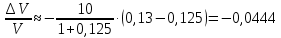
Это означает, что цена облигации понизилась на 4,44%.
12. Найти портфель из 3-летней и 6-летней облигаций иммунизирующий 4- летнюю облигацию с номинальной стоимостью 1600 у.е., если процентная ставка составляет 12%. (Ответ: иммунизирующий портфель состоит из 3-летней облигации номинальной стоимостью 952,381 у.е. и 6-летней облигации стоимостью 669,0133 у.е.) Оценивание облигаций в произвольный момент времени и в календарной шкале.
Решение:
Составим систему уравнений
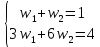
Вычитая из второго уравнения первое уравнение, умноженное на 3, получим 3w2 = 1
Следовательно
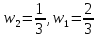. Теперь по очереди определим стоимости 4-летний, 6-летний и 3-летний облигации: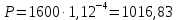
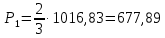
Найдем номинальные стоимости 3-летней и 6-летней облигации
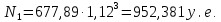
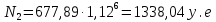
Ответ: 952,381 у.е., 1338,04 у.е.
13. Используя дисконтирование по схеме сложных процентов, найти текущую стоимость облигации с номиналом 2350 руб., купонной ставкой 11% с годовыми купонными платежами и сроком до погашения 1,5 года относительно номинальной ставки 12% с годовым периодом начисления процентов.
Решение:
В схеме сложных процентов цена облигации к моменту оценивания будет
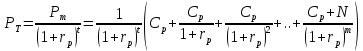
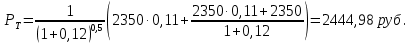
Ответ: текущая стоимость облигации 2444,98 руб.
14. Используя дисконтирование по схеме сложных процентов, найти текущую стоимость облигации с номиналом 1230 руб., купонной ставкой 10,5% с полугодовыми купонными платежами и сроком до погашения 1,2 года относительно номинальной ставки 12% с полугодовым периодом начисления процентов.
Решение:
В нашем случае срок до погашения 1,2 года в купонных периодах (полгода) равен Т = 2,4; число периодов до следующего купонного платежа равно t = 0,4
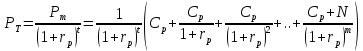
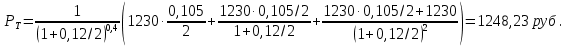
Ответ: текущая стоимость облигации равна 1248,23 руб.
15. Используя дисконтирование по схеме сложных процентов, найти чистую цену облигации с номиналом 3000 руб., купонной ставкой 11% с годовыми купонными платежами и сроком до погашения 1,4 года относительно номинальной ставки 12,5% с годовым периодом начисления процентов.
Решение:
В схеме сложных процентов цена облигации к моменту оценивания будет
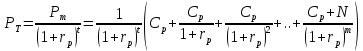
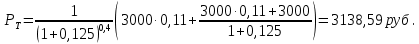
Чистая цена облигации равна
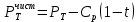
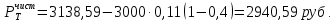
Ответ: чистая цена облигации равна 2940,59 руб.
16. Найти полную и чистую цену облигации с номиналом 3300 руб. с годовыми купонными платежами в середине последнего купонного периода при процентной ставке, равной 19,5% годовых и купонной ставке 19,8%.
Решение:
По условию задачи
N = 3300, p = 1, rp = 0,195 , Cp = cN/p = 0,198*3300 = 653.4; t =0,5
Цена облигации на следующую купонную выплату, т.е. на момент погашения равна
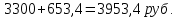
За полгода до этого ее полная цена стане равной
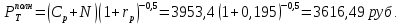
Номинальный купон к середине купонного периода
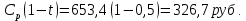
Таким образом, чистая цена облигации
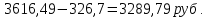
Ответ: полная цена составит 3616, 49 руб., чистая цена составит 3289,79 руб.
17. Найти накопленный купон по правилу ACT/365, если дата оценки облигации 25.06.20, а дата выплаты предыдущего купона 20.10.20. Купонный платеж 200 руб.
Решение:
Найдем номера дней оценивая и выплаты предыдущего купона
20.10.20 – 294
25.06.20 – 177
Тогда D = 294 – 177 = 117
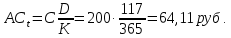
Ответ: накопленный купон будет равен 64,11 руб.
18. Найти накопленный купон по правилу ACT/360, если дата оценивания облигации 27.07.21, а дата выплаты предыдущего купона 18.04.21. Купонный платеж 300 руб.
Решение:
Найдем номера дней оценивая и выплаты предыдущего купона
27.07.21 – 208
18.04.21 – 108
Тогда D = 208 – 108 = 100
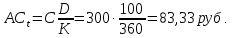
Ответ: накопленный купон будет равен 83,33 руб.
19. Найти накопленный купон по правилу 30/360, если дата оценки облигации 12.07.21, а дата выплаты предыдущего купона 16.04.21. Купонный платеж 350 руб.
Найдем номера дней оценивая и выплаты предыдущего купона
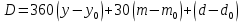
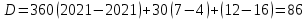
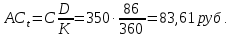
Ответ: накопленный купон будет равен 83,61 руб.
20. Найти накопленный купон по правилу ACT/ACT, если дата оценивания облигации 12.04.16, дата выплаты следующего купона 14.07.16. а дата выплаты предыдущего купона 19.01.16. Купонный платеж 230 руб.
Найдем номера дней оценивая и выплаты предыдущего купона
12.04.16 – 103
14.07.16 – 196
19.01.16 – 19
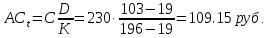
Ответ: накопленный купон будет равен 109.15 руб.
21. Найти параметр t по правилу ACT/365, если дата оценки облигации 20.10.17, а дата выплаты предыдущего годового купона 15.06.17.
Решение:
Следующая годовая купонная дата 15.06.18 имеет №166, дата оценивания 20.10.17 имеет № 293.
Тогда
