ЛЕКЦИЯ 5

Кривые второго порядка

цель лекции: ввести понятие кривых второго порядка, рассмотреть виды уравнений кривых второго порядка

ключевые слова (термины): Окружность, эллипс, гипербола, парабола, каноническое уравнение, эксцентриситет.

основные вопросы (положения) и краткое содержание

Для составления уравнений линий в декартовых координатах нужно задать определение или геометрические свойства этой линии и исходя из этого составить уравнение этой линии, т.е. связать между собой текущие координаты точек рассматриваемой линии.

Этим способом составим уравнения: окружности, эллипса, гиперболы и параболы.
Окружность

Окружностью называется геометрическое место точек на плоскости, равноудаленных от одной фиксированной точки плоскости, называемой центром окружности.

Пусть - центр окружности, R - её радиус, - произвольная точка окружности. На основании определения окружности и формулы расстояния между двумя точками имеем:



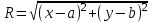
или 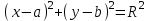(3.1)

Уравнение (3.1) называется простейшим или каноническим уравнением окружности.

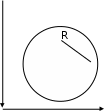У Если , то получается

уравнение окружности с центром




R


в начале координат, т.е.

(3.2)

---

x

Раскрывая скобки в уравнении (3.1) и перенося R² в левую часть, получим:



или (3.3)

где

Если уравнение окружности дано в виде (3.1) или (3.2), то сразу видно, что координаты центра окружности равны а и b, а радиус равен R.

Если уравнение окружности дано в виде (3.3), то

(3.4).

Уравнение (3.3) называется общим уравнением окружности и является уравнением второй степени.

Пример: Определить координаты центра и радиус окружности привести ее к простейшему виду.

Решение: Первый способ: используя формулу (3.4) находим координаты центра и радиус окружности. Так как , то



Тогда каноническое уравнение окружности будет иметь вид:

.

2 способ: преобразуем исходное уравнение следующим образом:

или .

Окончательно получим каноническое уравнение окружности в виде .

Т.е. координаты центра и радиус окружности равны: .
Эллипс
Эллипсом называется геометрическое место точек плоскости, сумма расстояний от каждой из которых до двух данных точек

---

и , называемых фокусами эллипса , есть величина постоянная ( ) , большая чем расстояние между фокусами.

Обозначим расстояние между фокусами . Это расстояние называется фокусным расстоянием. Для составления уравнения эллипса введем систему координат (рис.10). За начало координат примем середину отрезка , прямую - за ось OХ, а ось OУ проведем перпендикулярно к оси OХ. Тогда фокусы имеют координаты .

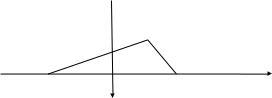у




х


Рис.1

Пусть произвольная точка эллипса. На основании определения эллипса имеем:

(3.5)

причем , т.е. или .

Обозначим

---

, тогда

(3.6)

Отрезки и - называются фокальными радиусами. Используя формулу расстояний между двумя точками на плоскости получим:

(3.7)

Поставив значения и в (3.6) получим:

(3.8)

Преобразуем уравнение (3.8):











или

так как 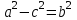, то, обозначив будем иметь

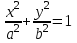(3.9)

Уравнение (3.9) называется каноническим уравнением эллипса.
Для исследования формы эллипса, выразим из уравнения (3.9) переменную у как функцию от x:

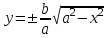(3.10)

Так эллипс симметричен относительно координатных осей, достаточно рассмотреть ту часть эллипса, которая расположена в первой четверти.

При

---

получим . Точка самая верхняя точка рассматриваемой линии. Пусть х возрастает, тогда при , получим, что .

При дальнейшем увеличении х, т.е. при , подкоренное выражение (3.10) будет отрицательным, у – мнимым . Следовательно точка является самой правой точкой исследуемого графика. Дуга ВА является четвертью эллипса (рис.11).

у у





х х



Рис.11 Рис.12
Произведя зеркальное отражение дуги ВА относительно осей координат, получим весь эллипс (Рис.12).

Отрезок называют большой полуосью эллипса, малой полуосью.

Из (3.8) путем элементарных преобразований можно получить:

или

Обозначим , тогда и

---

Смотрите также файлы

• 1. Понятие и признаки государства Государство.docx

• Июнь. Комплекс 1 Погремушки. Вводная часть.doc

• Курсовая работа Управление природопользованием в России.docx

• Петров Никита Владимирович.pdf

• Санды сауаттылы Педагогты атыжні.docx