Файл: Лекции ввести понятие кривых второго порядка, рассмотреть виды уравнений кривых второго порядка.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 57
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
. (3.15)
Прямые называются директрисами гиперболы.
называются директрисами гиперболы.
Так как для гиперболы , то
, то  . Это означает, что правая директриса расположена между центром и правой вершиной гиперболы, левая – между центром и левой вершиной.
. Это означает, что правая директриса расположена между центром и правой вершиной гиперболы, левая – между центром и левой вершиной.
 у
у




 х
х



Рис.14
Уравнение
 (3.16)
(3.16)
также является уравнением гиперболы, действительная ось которой лежит на оси ОУ, а мнимая ось
лежит на оси ОУ, а мнимая ось  лежит на оси ОХ.
лежит на оси ОХ.
Эксцентриситет этой гиперболы равен , асимптоты определяются уравнениями
, асимптоты определяются уравнениями  , а уравнения директрис
, а уравнения директрис  .
.
Гиперболы, определяемые уравнениями (3.13) и (3.16) называются сопряженными.
Уравнение гиперболы с осями, параллельными осям координат, имеет вид:
 (3.17) где
(3.17) где  - координаты центра гиперболы.
- координаты центра гиперболы.
Пример 1: Составить каноническое уравнение гиперболы и ее асимптоты, зная, что расстояние между фокусами , а эксцентриситет
, а эксцентриситет  .
.
Решение: Так как по условию и
и 
,
то и
и  .
.
По формуле имеем:
имеем:  ,
,
 . Поэтому уравнение гиперболы примет вид:
. Поэтому уравнение гиперболы примет вид:  .
.
Уравнение асимптот имеет вид: , т.е.
, т.е.  .
.
Пример 2. Составить уравнение гиперболы, если её фокусы лежат на оси ОУ и расстояние между ними равно 10, а действительная ось равна 8.
Решение. Так как фокусы гиперболы находятся на оси ОУ( т.е. ось ОУ будет действительной для гиперболы), то уравнение гиперболы будем искать в виде: .
.
По условию .
.
Из соотношения находим мнимую полуось:
находим мнимую полуось:
 .
.
Поэтому уравнение гиперболы примет вид: .
.
Пример 3. Найти уравнение гиперболы, фокусы которой находятся в точках и
и  , а мнимая ось равна 6.
, а мнимая ось равна 6.
Решение. Центром гиперболы будет середина отрезка , т.е. точка, координаты которой будут равны
, т.е. точка, координаты которой будут равны
 ,
, 
Уравнение гиперболы будем искать в виде:
 .
.
По условию . Расстояние между фокусами равно
. Расстояние между фокусами равно  .
.
Находим теперь действительную полуось: так как , то
, то 
.
Значит, уравнение гиперболы будет иметь вид:
 .
.
Парабола
Параболой называется геометрическое место точек плоскости, каждая из которых равноудалена от данной точки, называемой фокусом, и от данной прямой, называемой директрисой.
у



r
х


 Рис.15
Рис.15
Выведем каноническое уравнение параболы. За ось ОХ примем прямую, проходящую через точку F. Ось ОУ проведем перпендикулярно через середину отрезка и примем
и примем  . Следовательно, фокус имеет координаты
. Следовательно, фокус имеет координаты  , а уравнение директрисы
, а уравнение директрисы  .
.
Пусть произвольная точка параболы, тогда по определению параболы имеем
произвольная точка параболы, тогда по определению параболы имеем  или
или
 (3.18)
(3.18)
Избавляясь от иррациональности, получим:

или (3.19)
(3.19)
Уравнение (3.19) называется каноническим уравнением параболы.
Так как в уравнение (3.19) переменная у входит в четной степени, то парабола симметрична относительно оси ОХ, сама ось ОХ является осью симметрии параболы.
При получим
получим  , значит, парабола проходит через начало координат. Точка
, значит, парабола проходит через начало координат. Точка  является вершиной параболы. Если
является вершиной параболы. Если  , то ветви параболы направлены вправо, при
, то ветви параболы направлены вправо, при
 ветви направлены влево.
ветви направлены влево.
Длина отрезка называется фокальным радиусом точки М. Фокальный радиус вычисляется по формуле
называется фокальным радиусом точки М. Фокальный радиус вычисляется по формуле
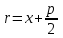 (3.20)
(3.20)
Уравнение (3.21)
(3.21)
также является каноническим уравнением параболы.
Парабола, определяемая уравнением (3.21) симметрична относительно оси ОУ; вершина находится в точке ; ветви направлены вверх при
; ветви направлены вверх при  и вниз при
и вниз при  .
.
Фокус такой параболы находится в точке , уравнение директрисы имеет вид
, уравнение директрисы имеет вид  , фокальный радиус равен
, фокальный радиус равен  (3.22)
(3.22)
Если парабола имеет осями симметрии прямые, параллельные осям координат, то уравнение параболы примет вид:
 (3.23)
(3.23)
или
 (3.24)
(3.24)
где - координаты вершины параболы.
- координаты вершины параболы.
Пример 1. Составить уравнение параболы зная, что она симметрична относительно оси ОХ и проходит через начало координат и точку .
.
Решение: Подставив координаты точки в уравнение (3.19), получим
в уравнение (3.19), получим  , откуда
, откуда  .
.
Тогда уравнение параболы примет вид: .
.
Пример 2. Дана парабола . Найти координаты её фокуса, уравнение директрисы, длину фокального радиуса точки
. Найти координаты её фокуса, уравнение директрисы, длину фокального радиуса точки  .
.
Решение. Парабола задана каноническим уравнением (3.21). Находим р:
.
Поэтому фокус параболы будет иметь координаты , а уравнение директрисы будет иметь вид:
, а уравнение директрисы будет иметь вид:  .
.
Фокальный радиус точки найдем по формуле (3.22):
найдем по формуле (3.22):
 .
.
Пример 3. Найти вершину, фокус и директрису параболы .
.
Решение. Преобразуем данное уравнение, выделив полный квадрат из квадратного трехчлена:
 .
.
Значит или
или  .
.
Уравнение параболы имеет вид (3.24). Вершина этой параболы находится в точке ;
;  , т.е.
, т.е.  .
.
Прямая является осью симметрии параболы, фокус имеет координаты
является осью симметрии параболы, фокус имеет координаты  , т.е.
, т.е.  .
.
Уравнение директрисы , т.е
, т.е  .
.
Вопросы для самоконтроля:
критерии оценки достижения обучающимися результатов обучения:
Даны в силлабусе.
рекомендуемая литература: Дана в силлабусе.
Прямые
 называются директрисами гиперболы.
называются директрисами гиперболы.Так как для гиперболы
 , то
, то  . Это означает, что правая директриса расположена между центром и правой вершиной гиперболы, левая – между центром и левой вершиной.
. Это означает, что правая директриса расположена между центром и правой вершиной гиперболы, левая – между центром и левой вершиной. у
у



 х
х


Рис.14
Уравнение
 (3.16)
(3.16)также является уравнением гиперболы, действительная ось которой
 лежит на оси ОУ, а мнимая ось
лежит на оси ОУ, а мнимая ось  лежит на оси ОХ.
лежит на оси ОХ.Эксцентриситет этой гиперболы равен
 , асимптоты определяются уравнениями
, асимптоты определяются уравнениями  , а уравнения директрис
, а уравнения директрис  .
.Гиперболы, определяемые уравнениями (3.13) и (3.16) называются сопряженными.
Уравнение гиперболы с осями, параллельными осям координат, имеет вид:
 (3.17) где
(3.17) где  - координаты центра гиперболы.
- координаты центра гиперболы.Пример 1: Составить каноническое уравнение гиперболы и ее асимптоты, зная, что расстояние между фокусами
 , а эксцентриситет
, а эксцентриситет  .
. Решение: Так как по условию
 и
и 
,
то
 и
и  .
. По формуле
 имеем:
имеем:  ,
,
 . Поэтому уравнение гиперболы примет вид:
. Поэтому уравнение гиперболы примет вид:  .
. Уравнение асимптот имеет вид:
 , т.е.
, т.е.  .
. Пример 2. Составить уравнение гиперболы, если её фокусы лежат на оси ОУ и расстояние между ними равно 10, а действительная ось равна 8.
Решение. Так как фокусы гиперболы находятся на оси ОУ( т.е. ось ОУ будет действительной для гиперболы), то уравнение гиперболы будем искать в виде:
 .
.По условию
 .
.Из соотношения
 находим мнимую полуось:
находим мнимую полуось: .
.Поэтому уравнение гиперболы примет вид:
 .
.Пример 3. Найти уравнение гиперболы, фокусы которой находятся в точках
 и
и  , а мнимая ось равна 6.
, а мнимая ось равна 6.Решение. Центром гиперболы будет середина отрезка
 , т.е. точка, координаты которой будут равны
, т.е. точка, координаты которой будут равны ,
, 
Уравнение гиперболы будем искать в виде:
 .
.По условию
 . Расстояние между фокусами равно
. Расстояние между фокусами равно  .
. Находим теперь действительную полуось: так как
 , то
, то 
.
Значит, уравнение гиперболы будет иметь вид:
 .
.Парабола
Параболой называется геометрическое место точек плоскости, каждая из которых равноудалена от данной точки, называемой фокусом, и от данной прямой, называемой директрисой.
у


r
х


 Рис.15
Рис.15Выведем каноническое уравнение параболы. За ось ОХ примем прямую, проходящую через точку F. Ось ОУ проведем перпендикулярно через середину отрезка
 и примем
и примем  . Следовательно, фокус имеет координаты
. Следовательно, фокус имеет координаты  , а уравнение директрисы
, а уравнение директрисы  .
. Пусть
 или
или  (3.18)
(3.18) Избавляясь от иррациональности, получим:

или
 (3.19)
(3.19) Уравнение (3.19) называется каноническим уравнением параболы.
Так как в уравнение (3.19) переменная у входит в четной степени, то парабола симметрична относительно оси ОХ, сама ось ОХ является осью симметрии параболы.
При
 получим
получим  , значит, парабола проходит через начало координат. Точка
, значит, парабола проходит через начало координат. Точка  является вершиной параболы. Если
является вершиной параболы. Если  , то ветви параболы направлены вправо, при
, то ветви параболы направлены вправо, при
 ветви направлены влево.
ветви направлены влево.Длина отрезка
 называется фокальным радиусом точки М. Фокальный радиус вычисляется по формуле
называется фокальным радиусом точки М. Фокальный радиус вычисляется по формуле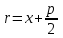 (3.20)
(3.20)Уравнение
 (3.21)
(3.21) также является каноническим уравнением параболы.
Парабола, определяемая уравнением (3.21) симметрична относительно оси ОУ; вершина находится в точке
 ; ветви направлены вверх при
; ветви направлены вверх при  и вниз при
и вниз при  .
. Фокус такой параболы находится в точке
 , уравнение директрисы имеет вид
, уравнение директрисы имеет вид  , фокальный радиус равен
, фокальный радиус равен  (3.22)
(3.22)Если парабола имеет осями симметрии прямые, параллельные осям координат, то уравнение параболы примет вид:
 (3.23)
(3.23) или
 (3.24)
(3.24) где
 - координаты вершины параболы.
- координаты вершины параболы.Пример 1. Составить уравнение параболы зная, что она симметрична относительно оси ОХ и проходит через начало координат и точку
 .
.Решение: Подставив координаты точки
 в уравнение (3.19), получим
в уравнение (3.19), получим  , откуда
, откуда  .
.Тогда уравнение параболы примет вид:
 .
.Пример 2. Дана парабола
 . Найти координаты её фокуса, уравнение директрисы, длину фокального радиуса точки
. Найти координаты её фокуса, уравнение директрисы, длину фокального радиуса точки  .
.Решение. Парабола задана каноническим уравнением (3.21). Находим р:

.
Поэтому фокус параболы будет иметь координаты
 , а уравнение директрисы будет иметь вид:
, а уравнение директрисы будет иметь вид:  .
.Фокальный радиус точки
 найдем по формуле (3.22):
найдем по формуле (3.22):  .
.Пример 3. Найти вершину, фокус и директрису параболы
 .
.Решение. Преобразуем данное уравнение, выделив полный квадрат из квадратного трехчлена:
 .
.Значит
 или
или  .
.Уравнение параболы имеет вид (3.24). Вершина этой параболы находится в точке
 ;
;  , т.е.
, т.е.  .
. Прямая
 является осью симметрии параболы, фокус имеет координаты
является осью симметрии параболы, фокус имеет координаты  , т.е.
, т.е.  .
.Уравнение директрисы
 , т.е
, т.е  .
.Вопросы для самоконтроля:
-
Определение окружности. -
Каноническое уравнение окружности. -
Определение эллипса, его каноническое уравнение. -
Полуоси, фокусы, эксцентриситет эллипса. -
Определение гиперболы, её каноническое уравнение. -
Полуоси, фокусы, эксцентриситет, уравнения асимптот гиперболы. -
Определение параболы, её канонические уравнения. -
Фокус, директриса параболы.
критерии оценки достижения обучающимися результатов обучения:
Даны в силлабусе.
рекомендуемая литература: Дана в силлабусе.