решений рассматривают в разделах, связанных с изучением экстремумов функций, в математическом программировании.

Методы оптимальных решений является одним из разделов исследования операций, используемого для решения практических организационных задач. Задачи математического программирования находят применение в различных областях человеческой деятельности, где необходим выбор одного из возможных образов действий (программ действий).

Среди  методов   математического   программирования  наиболее полно разработанными и распространенными в производственной практике являются методы линейного программирования.

Целью данной курсовой работы является овладение математическими методами решения экономических задач.

Задачи курсовой работы:

- научиться строить экономико-математические модели основных типов задач линейного программирования и решать данные задачи с помощью надстройки Microsoft Excel «Поиск решения»;

- освоить графический метод решения  задачи линейного программирования;

- освоить симплекс-метод и метод решения задачи линейного программирования.

В первой части курсовой работы на тему «Модели организации и планирования производства» будут рассмотрены следующие вопросы: определения линейного программирования и математической модели; правила составления математической модели; виды математических моделей и основные типы задач линейного программирования (ЗЛП); что такое переменные, целевая функция и ограничения задачи.

Во второй и третьей части курсовой работы будут представлены производственные задачи, их математические модели, решение графическим и симплекс-методом, а также решение с использованием надстройки «Поиск решения» Мicrosoft Excel.

1. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ, МЕТОДЫ ОПТИМАЛЬНЫХ РЕШЕНИЙ, ИХ СВОЙСТВА И ПРИМЕНЕНИЕ В ПЛАНИРОВАНИИ ПРОИЗВОДСТВА
Первые постановки задач линейного программирования были сформулированы известным советским математиком-экономистом Л.В. Канторовичем в 1939 году, которому за эти работы была присуждена Нобелевская премия по экономике. Появление этой работы открыло новый этап в применении математики в экономике. В 1947 году математик Дж. Данциг разработал эффективный метод решения данного класса задач – симплекс-метод.

Линейное программирование

---

— это наука о методах исследования и отыскания экстремальных (наибольших и наименьших) значений линейной функции, на неизвестные которой наложены линейные ограничения. Для решения задач линейного программирования составляется математическая модель задачи и выбирается метод решения. По типу решаемых задач методы разделяются на универсальные и специальные. С помощью универсальных методов могут решаться любые задачи линейного программирования (ЗЛП). Специальные методы учитывают особенности модели задачи, ее целевой функции и системы ограничений.

Перед решением задачи составляем её математическую модель.

Математической моделью называется математическое выражение целевой функции и ее ограничений.

Принцип составления математической модели следующий:

- в первую очередь необходимо определить критерий оптимальности (максимум прибыли, минимум издержек и т.д.);

- во втором этапе для построения математической модели необходимо задать переменные решения;

- третьим этапом составления математической модели будет определение целевой функции;

- завершающим этапом будет определение условия, ограничивающие изменения переменных решения в процессе поиска оптимума целевой функции – ограничения задачи (уравнения или неравенства).

Критерий оптимальности – это характерный показатель решения задачи, по значению которого оценивается оптимальность найденного решения, то есть максимальное удовлетворение поставленным требованиям.

Переменными задачи называются величины х₁, х₂,…,х_n, которые полностью характеризуют экономический процесс, описанный в задаче.

Целевая функция – это функция Z(X), которая характеризует качество выполнения задачи, экстремум которой надо найти.

Z(X) = С1Х1+С2Х2+...+СnХnmax(min),

где C_n — заданные постоянные величины.

Ограничения, которые математически записываются в виде уравнений или неравенств, называются системой ограничений.

В общем виде математическая модель задачи линейного программирования (ЗЛП) записывается так:

Z(X) = С1Х1+С2Х2+...+СnХnmax(min)





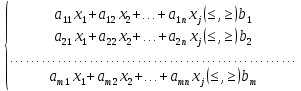
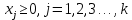
Допустимым решением (планом) задачи линейного программирования называется вектор X = (х

---

₁, х₂,..., х_n), удовлетворяющий системе ограничений.

Множество допустимых решений образует область допустимых решений задачи (ОДР).

Оптимальным решением называется допустимое решение задачи, при котором целевая функция достигает экстремума.

Графический метод решения задач линейного программирования можно применять, если количество неизвестных в задаче равно двум. В общем виде задачи линейного программирования с двумя переменными

Z(X) = с₀+с₁х₁+с₂х₂max(min)





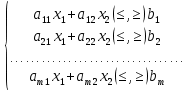
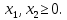
Область допустимых решений системы ограничений (ОДР) имеет вид выпуклого многоугольника (или неограниченной выпуклой многоугольной области), что позволяет легко построить данное множество на плоскости.

Стороны такого многоугольника лежат на прямых, полученных из системы ограничений задачи:



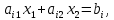
где i – 1,…,m.

Экстремальные значения целевой функции следует искать среди угловых точек (вершин) области допустимых решений.

Алгоритм графического метода решения задачи линейного программирования:

- построить область допустимых решений (ОДР);

- построить вектор градиента gradZ=(c₁, c₂) целевой функции;

- построить линии уровня целевой функции, перпендикулярные вектору градиента (графический поиск экстремальных точек);

- определить аналитически координаты экстремальных точек и вычислить значение целевой функции в них.

Задачи, решаемые методами линейного программирования, очень разнообразны по содержанию. Но их математические модели схожи и условно объединяются в следующие группы задач:

- задачи об оптимальном распределении ресурсов (оптимальная производственная программа);

- задачи об оптимальной корзине продуктов;

- задачи оптимального раскроя;

- задачи составления расписания;

- транспортные задачи;

- задачи о назначениях.

Широкое применение модели линейного программирования получили при решении задач экономии ресурсов (выбор ресурсосберегающих технологий, составление смесей), производственных и других задач.

---

Далее рассмотрим еще один метод оптимальных решений – симплекс-метод. Данный метод позволяет решать задачи линейного программирования с любым количеством переменных.

Правила пересчета симплекс-метода:

- на месте генерального элемента пишется величина ему обратная;

- все элементы генеральной строки (кроме генерального элемента) делятся на генеральный элемент;

- все элементы генерального столбца (кроме генерального элемента) делятся на генеральный элемент и берутся с противоположным знаком;

- все остальные элементы пересчитываются по правилу прямоугольника:





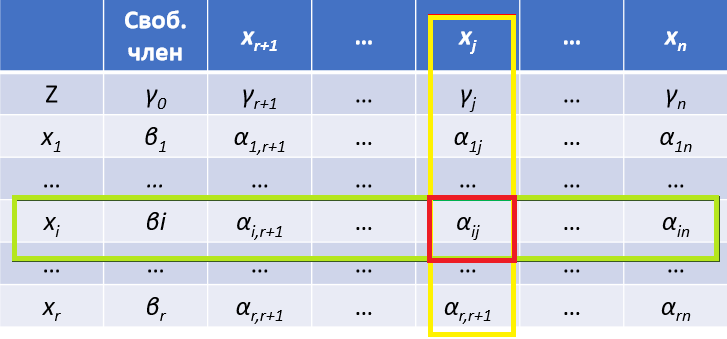
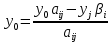
Суть симплекс-метода состоит в целенаправленном последовательном улучшении решений с учетом изменений целевой функции.

Если все ограничения системы заданы уравнениями и переменными неотрицательные, то такая модель задачи линейного программирования называется канонической. Если хотя бы одно ограничение является неравенством, то модель задачи является неканонической.

Чтобы перейти от неканонической модели к канонической, необходимо в каждое неравенство ввести балансовую переменную. В целевую функцию балансовые переменные не вводятся. Кроме того, если правая часть какого-либо ограничения отрицательна, то обе части данного ограничения необходимо домножить на (-1). Также будем полагать, что целевую функцию необходимо минимизировать.

2. КЕЙС-ЗАДАНИЕ №1. ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ: ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ
Предприятие выпускает два вида крепежных изделий: гайки и шайбы. Норма расхода сырья, времени работы оборудования и затрат на электроэнергию, которые необходимы для производства одной тонны каждого изделия, приведены в таблице.

Месячные запасы ресурсов, которыми располагает предприятие, ограничены. По сырью эти ограничения обусловлены емкостью складских помещений, по оборудованию – станочным парком и трудовыми ресурсами, по электроэнергии – техническими и финансовыми причинами. Размеры запасов и прибыль от реализации продукции в у.е. за 1 тонну приведены в таблице.

---

Ресурсы	Нормы расхода ресурсов на тонну продукции		Ограничения по ресурсам
	Шайбы	Гайки
Сырье	4	6,4	316
Оборудование	3,2	4,8	266
Электроэнергия	4	5,6	240
Прибыль (у.е./т)	90	140

Требуется сформировать месячную производственную программу (определить объемы выпуска каждого вида продукции), при которой прибыль от реализации будет максимальной. Составить математическую модель данной задачи и решить ее двумя способами:
а) графическим методом;

Построение математической модели.

Критерий оптимальности – максимальный доход.

Переменные решения:

х₁ – объем выпуска крепежного изделия – шайбы, (тонн);

х₂ – объем выпуска крепежного изделия – гайки, (тонн);

Цель – максимизация прибыли, получаемая при реализации крепежных изделий: шайб и гаек. Таким образом, суммарная прибыль, то есть целевая функция:

Z(X) = 90х₁+140х₂max

Ограничения по запасам ресурса на три вида продукции.

Левая часть ограничения по нормам расхода ресурсов представляет собой сырье, оборудование и электроэнергию, затрачиваемые на производство объема выпуска каждого вида крепежных изделий х₁, х₂. Правая часть ограничения – это их запас ресурса. Получаем следующие ограничения:

- по сырью:

4х₁ + 6,4х₂ ≤ 316;

- по оборудованию:

3,2х₁ + 4,8х₂ ≤ 266;

- по электроэнергии:

4х₁ + 5,6х₂ ≤ 240.

Данная математическая модель выглядит следующим образом:

Z(X) = 90х₁+140х₂  max





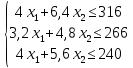
Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).

Построим уравнение 4x₁+6,4x₂

---

Смотрите также файлы

• Тесты тут httpst mehelp synergy По назначению и характеру использования информационные технологии.pdf

• Состав, структура и динамика основных средств ооо "жкх холмогоры".doc

• Применение радиоактивных изотопов в сельском хозяйстве.docx

• Вопросы к экзамену Роль экономического анализа в управлении и последовательность его проведения.docx

• Срок прохождения практики с 20 г по 20 г.docx