Файл: Решений рассматривают в разделах, связанных с изучением экстремумов функций, в математическом программировании.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 48
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
=316 по двум точкам. Для нахождения первой точки приравниваем x1=0. Находим x2 = 49,375. Для нахождения второй точки приравниваем x2=0. Находим x1=79.
Соединяем точку (0;49,375) с (79;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0;0), определим знак неравенства в полуплоскости: 4*0+6,4*0≤316, т.е. 4x1+6,4x2≤316 в полуплоскости ниже прямой.
Далее построим уравнение 3,2x1+4,8x2=266 по двум точкам (по вышеизложенному алгоритму).
Соединяем точку (0;55,416) с (83,125;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0;0), определим знак неравенства в полуплоскости: 3,2*0+4,8*0≤266, т.е. 3,2x1+4,8x2≤266 в полуплоскости ниже прямой.
Построим уравнение 4x1+5,6x2=240 по двум точкам.
Соединяем точку (0;42,8571) с (60;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0;0), определим знак неравенства в полуплоскости: 4*0+5,6*0≤240, т.е. 4x1+5,6x2≤240 в полуплоскости ниже прямой.
Исходя их нашей целевой функции задачи Z(X) = 90х1+140х2 max, можем найти вектор-градиент. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации Z(X). Начало вектора – точка (0; 0), конец – точка (90;140).
gradZ = (90;140)
Поскольку вектор-градиент пересекается с прямой (3), находим максимальную величину (xmax).
4x1+5,6x2=240
Решив систему уравнений, получим:
x1=0,
x2=42,8571.
Откуда найдем максимальное значение целевой функции:
Z(X) = 90*0+140*42,8571 = 6000
Исходя из вышеизложенного решения графическим методом, график решения выглядит следующим образом:
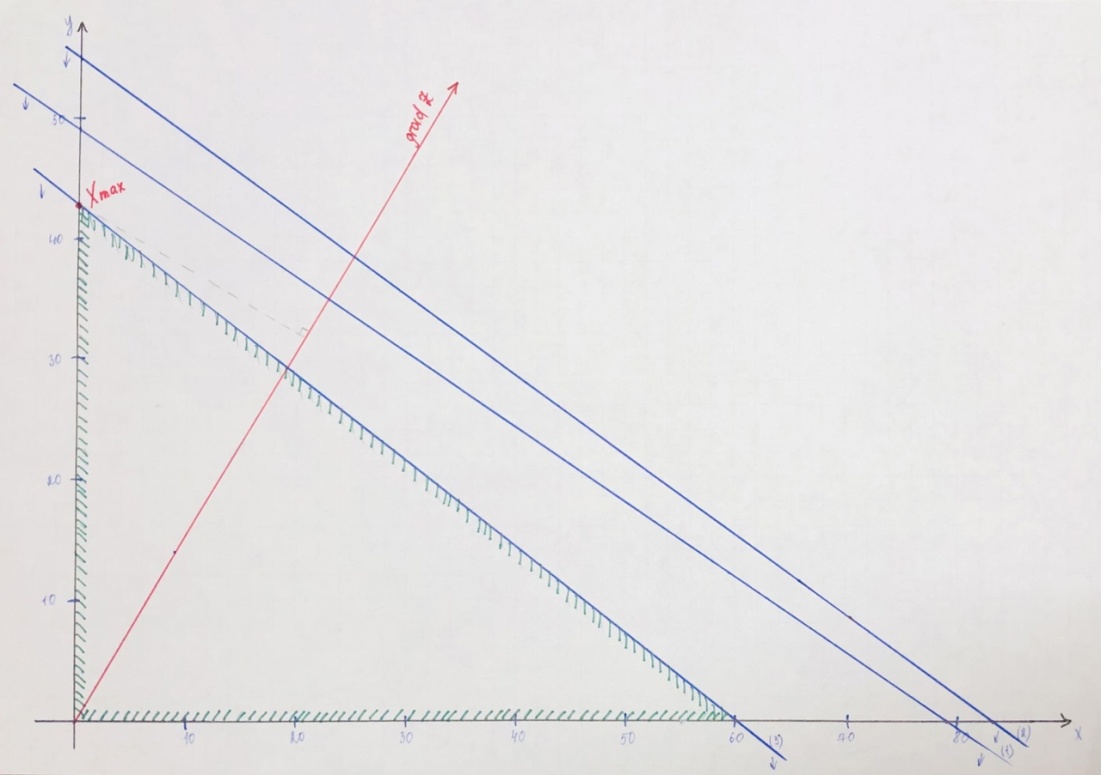
Вывод: при объеме выпуска 0 тонн шайб, 42,8571 тонн гаек, максимальная прибыль от реализации крепежных изделий составит 6000 у.е.
б) с использованием надстройки «Поиск решения» MSExcel.
Построив математическую модель, можно перейти к построению табличной модели. Для этого введем данные – параметры, которые характеризуют выпуск крепежных изделий, в единую таблицу.
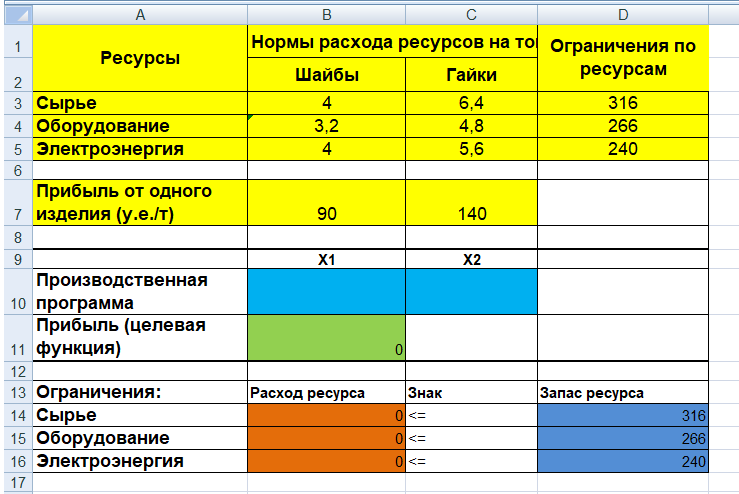
В колонке «Запас ресурса» указаны ограниченные месячные запасы ресурсов, которыми располагает предприятие.
Целевая функция. В ячейке В11 будет отображаться значение целевой функции. Формула, по которой это значение будет рассчитано, определяется выражением:
90х1+140х2
Используя обозначения соответствующих ячеек в Excel, получим следующее:
=СУММПРОИЗВ(B10:C10;B7:C7)
Ограничения задачи представляют собой сумму произведений каждой из ячеек переменных (B10, C10) на соответствующую ячейку для коэффициентов конкретного ограничения (B7, C7).
Таким образом, для первого ограничения в ячейку В14 будет введена формула:
=СУММПРОИЗВ($B$10:$C$10;B3:C3),
где символ $ означает, что при копировании этой формулы в другие места листа Excel номер строки 10 не изменится. Скопируем эту формулу в ячейки В15 и В16. В формуле будет меняться только номер строки во втором массиве. Этот номер является строкой, где записано ограничение.
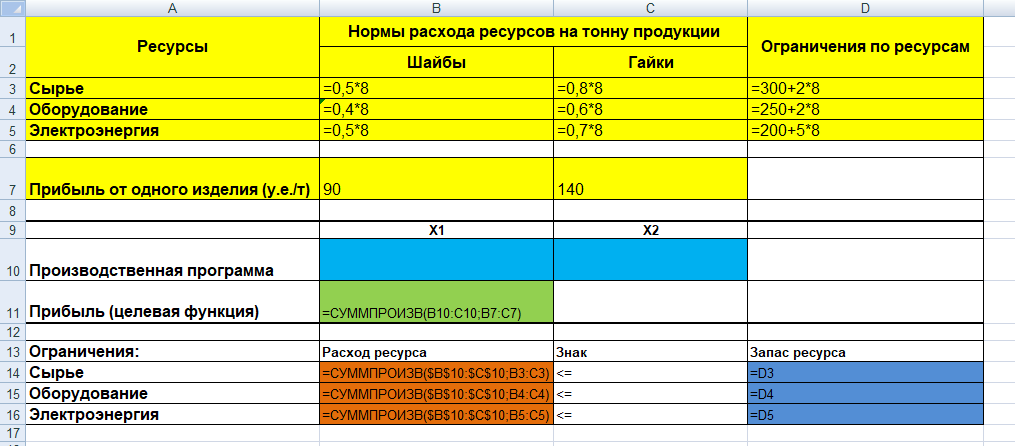
С помощью надстройки «Поиск решения» найдем решение данной задачи. В диалоговом окне «Поиска решения» требуется ввести необходимые параметры.
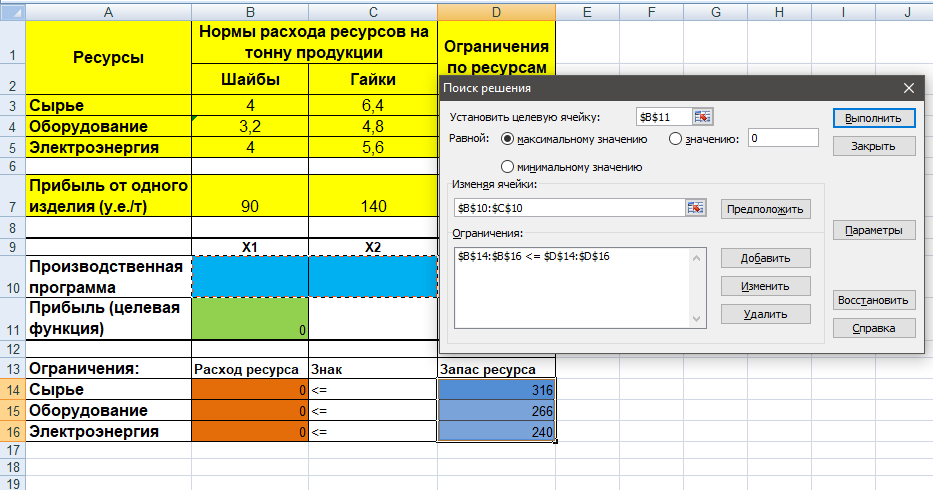
Результаты поиска решения следующие:
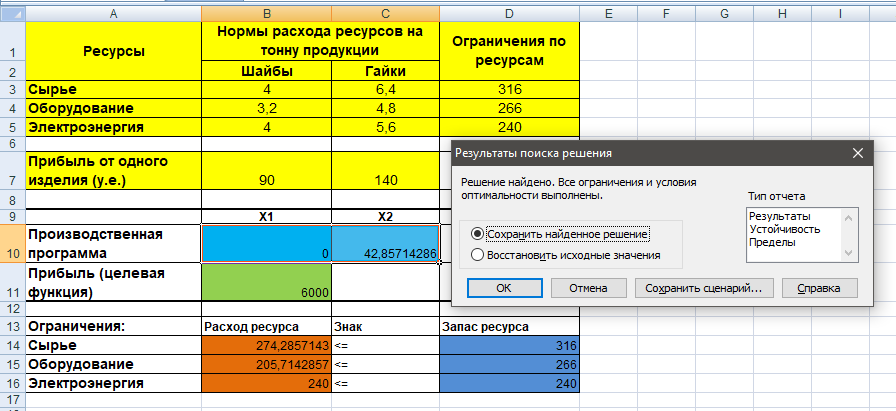
Вывод: при объеме выпуска 0 тонн шайб, 42,8571 тонн гаек, максимальная прибыль от реализации крепежных изделий составит 6000 у.е.
3. КЕЙС-ЗАДАНИЕ №2. СИМПЛЕКС-МЕТОД
Предприятие выпускает три вида крепежных изделий: гайки, болты и шайбы. Норма расхода сырья, времени работы оборудования и затрат на электроэнергию, которые необходимы для производства одной тонны каждого изделия, приведены в таблице. Месячные запасы ресурсов, которыми располагает предприятие, ограничены. По сырью эти ограничения обусловлены емкостью складских помещений, по оборудованию – станочным парком и трудовыми ресурсами, по электроэнергии – техническими и финансовыми причинами. Спрос на шайбы не превосходит 0,625т, а спрос на гайки не превышает 8т. Размеры запасов и прибыль от реализации продукции в у.е. за 1 тонну приведены в таблице.
Требуется сформировать месячную производственную программу (определить объемы выпуска каждого вида продукции), при которой прибыль от реализации будет максимальным.
Составить математическую модель данной задачи и решить ее двумя способами:
а) симплекс-методом;
Построение математической модели.
Критерий оптимальности – максимальный доход.
Переменные решения:
х1 – объем выпуска крепежного изделия – шайбы, (тонн);
х2 – объем выпуска крепежного изделия – гайки, (тонн);
х3 – объем выпуска крепежного изделия – болты, (тонн).
Цель – максимизация прибыли, получаемая при реализации крепежных изделий: шайб, гаек и болтов. Таким образом, суммарная прибыль, то есть целевая функция:
Z(X) = 90х1+140х2+200х3 max,
Ограничения по запасам ресурса на три вида продукции.
Левая часть ограничения по нормам расхода ресурсов представляет собой сырье, оборудование и электроэнергию, затрачиваемые на производство объема выпуска каждого вида крепежных изделий х1, х2, х3. Правая часть ограничения – это их запас ресурса. Получаем следующие ограничения:
- по сырью:
4х1 + 6,4х2+8,8х3 ≤ 316;
- по оборудованию:
3,2х1 + 4,8х2 +8х3 ≤ 266;
- по электроэнергии:
4х1 + 5,6х2 +7,2х3 ≤ 240.
Данная математическая модель выглядит следующим образом:
Z(X) = 90х1+140х2+200х3 max
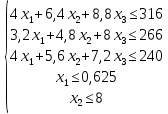
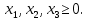
Приведем задачу линейного программирования к каноническому виду:
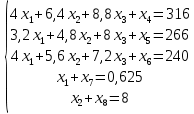
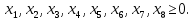
Далее, стандартная форма записи допустимого базисного решения будет иметь следующий вид:
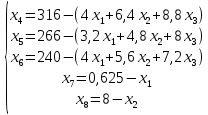
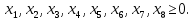
Следовательно: Z1(X) = 0-(90х1+140х2+200х3) min
Данному базисному решению соответствует следующая симплекс-таблица:
Нашли генеральный элемент – 8, так как в строке Z выбираем положительное число (у нас число 200 – выбираем столбец х3), а в столбце х3, не считая строки Z, выбираем то значение, для которого отношение к нему свободного члена минимально (266/8 – минимальное значение). В новом допустимом базисном решении х3 и х5 изменим на противоположные. Найдем это решение, перейдя к новой симплекс-таблице:
Определяем генеральный элемент в новой таблице – 1,28. В новом допустимом базисном решении х2 и х6 изменим на противоположные. Найдем это решение, перейдя к новой симплекс-таблице:
Далее генеральный столбец выбрать нельзя. Значит, оптимальное решение имеет вид Хопт=(0; 0,46875; 32,96875; 22,875; 0; 0; 0,625; 7,53125), Zmin=-6659,375.
Xmax=(0; 0,46875; 32,96875)
Zmax=6659,375.
Так как в условии задачи указано, что спрос на шайбы не превосходит 0,625т, а спрос на гайки не превышает 8т, то мы полностью удовлетворяем условие задачи.
Вывод: при объеме выпуска 0 тонн шайб, 0,46875 тонн гаек и 32,96875 тонн болтов максимальная прибыль от реализации крепежных изделий составит 6659,375 у.е.
б) с использованием надстройки «Поиск решения» MSExcel.
Построив математическую модель, можно перейти к построению табличной модели. Для этого введем данные – параметры, которые характеризуют выпуск крепежных изделий, в единую таблицу.
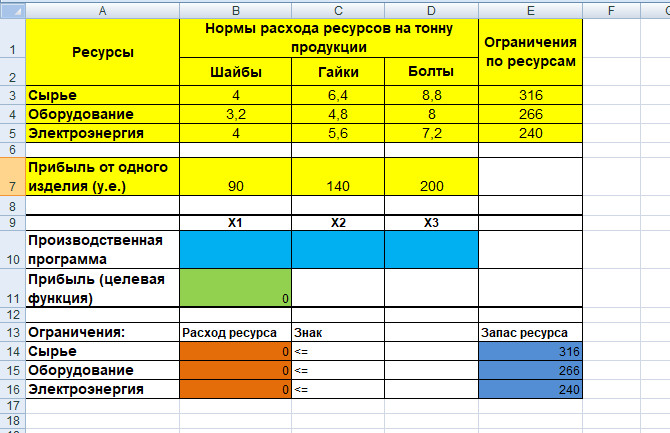
В колонке «Запас ресурса» указаны ограниченные месячные запасы ресурсов, которыми располагает предприятие. Целевая функция. В ячейке В11 будет отображаться значение целевой функции. Формула, по которой это значение будет рассчитано, определяется выражением:
| х1 | 0 | 79 |
| х2 | 49,375 | 0 |
Соединяем точку (0;49,375) с (79;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0;0), определим знак неравенства в полуплоскости: 4*0+6,4*0≤316, т.е. 4x1+6,4x2≤316 в полуплоскости ниже прямой.
Далее построим уравнение 3,2x1+4,8x2=266 по двум точкам (по вышеизложенному алгоритму).
| х1 | 0 | 83,125 |
| х2 | 55,416 | 0 |
Соединяем точку (0;55,416) с (83,125;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0;0), определим знак неравенства в полуплоскости: 3,2*0+4,8*0≤266, т.е. 3,2x1+4,8x2≤266 в полуплоскости ниже прямой.
Построим уравнение 4x1+5,6x2=240 по двум точкам.
| х1 | 0 | 60 |
| х2 | 42,8571 | 0 |
Соединяем точку (0;42,8571) с (60;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0;0), определим знак неравенства в полуплоскости: 4*0+5,6*0≤240, т.е. 4x1+5,6x2≤240 в полуплоскости ниже прямой.
Исходя их нашей целевой функции задачи Z(X) = 90х1+140х2 max, можем найти вектор-градиент. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации Z(X). Начало вектора – точка (0; 0), конец – точка (90;140).
gradZ = (90;140)
Поскольку вектор-градиент пересекается с прямой (3), находим максимальную величину (xmax).
4x1+5,6x2=240
Решив систему уравнений, получим:
x1=0,
x2=42,8571.
Откуда найдем максимальное значение целевой функции:
Z(X) = 90*0+140*42,8571 = 6000
Исходя из вышеизложенного решения графическим методом, график решения выглядит следующим образом:

Вывод: при объеме выпуска 0 тонн шайб, 42,8571 тонн гаек, максимальная прибыль от реализации крепежных изделий составит 6000 у.е.
б) с использованием надстройки «Поиск решения» MSExcel.
Построив математическую модель, можно перейти к построению табличной модели. Для этого введем данные – параметры, которые характеризуют выпуск крепежных изделий, в единую таблицу.

В колонке «Запас ресурса» указаны ограниченные месячные запасы ресурсов, которыми располагает предприятие.
Целевая функция. В ячейке В11 будет отображаться значение целевой функции. Формула, по которой это значение будет рассчитано, определяется выражением:
90х1+140х2
Используя обозначения соответствующих ячеек в Excel, получим следующее:
=СУММПРОИЗВ(B10:C10;B7:C7)
Ограничения задачи представляют собой сумму произведений каждой из ячеек переменных (B10, C10) на соответствующую ячейку для коэффициентов конкретного ограничения (B7, C7).
Таким образом, для первого ограничения в ячейку В14 будет введена формула:
=СУММПРОИЗВ($B$10:$C$10;B3:C3),
где символ $ означает, что при копировании этой формулы в другие места листа Excel номер строки 10 не изменится. Скопируем эту формулу в ячейки В15 и В16. В формуле будет меняться только номер строки во втором массиве. Этот номер является строкой, где записано ограничение.

С помощью надстройки «Поиск решения» найдем решение данной задачи. В диалоговом окне «Поиска решения» требуется ввести необходимые параметры.

Результаты поиска решения следующие:

Вывод: при объеме выпуска 0 тонн шайб, 42,8571 тонн гаек, максимальная прибыль от реализации крепежных изделий составит 6000 у.е.
3. КЕЙС-ЗАДАНИЕ №2. СИМПЛЕКС-МЕТОД
Предприятие выпускает три вида крепежных изделий: гайки, болты и шайбы. Норма расхода сырья, времени работы оборудования и затрат на электроэнергию, которые необходимы для производства одной тонны каждого изделия, приведены в таблице. Месячные запасы ресурсов, которыми располагает предприятие, ограничены. По сырью эти ограничения обусловлены емкостью складских помещений, по оборудованию – станочным парком и трудовыми ресурсами, по электроэнергии – техническими и финансовыми причинами. Спрос на шайбы не превосходит 0,625т, а спрос на гайки не превышает 8т. Размеры запасов и прибыль от реализации продукции в у.е. за 1 тонну приведены в таблице.
| Ресурсы | Нормы расхода ресурсов на тонну продукции | Ограничения по ресурсам | ||
| Шайбы | Гайки | Болты | ||
| Сырье | 4 | 6,4 | 8,8 | 316 |
| Оборудование | 3,2 | 4,8 | 1 | 266 |
| Электроэнергия | 4 | 5,6 | 7,2 | 240 |
| Прибыль (у.е./т) | 90 | 140 | 200 | |
Требуется сформировать месячную производственную программу (определить объемы выпуска каждого вида продукции), при которой прибыль от реализации будет максимальным.
Составить математическую модель данной задачи и решить ее двумя способами:
а) симплекс-методом;
Построение математической модели.
Критерий оптимальности – максимальный доход.
Переменные решения:
х1 – объем выпуска крепежного изделия – шайбы, (тонн);
х2 – объем выпуска крепежного изделия – гайки, (тонн);
х3 – объем выпуска крепежного изделия – болты, (тонн).
Цель – максимизация прибыли, получаемая при реализации крепежных изделий: шайб, гаек и болтов. Таким образом, суммарная прибыль, то есть целевая функция:
Z(X) = 90х1+140х2+200х3 max,
Ограничения по запасам ресурса на три вида продукции.
Левая часть ограничения по нормам расхода ресурсов представляет собой сырье, оборудование и электроэнергию, затрачиваемые на производство объема выпуска каждого вида крепежных изделий х1, х2, х3. Правая часть ограничения – это их запас ресурса. Получаем следующие ограничения:
- по сырью:
4х1 + 6,4х2+8,8х3 ≤ 316;
- по оборудованию:
3,2х1 + 4,8х2 +8х3 ≤ 266;
- по электроэнергии:
4х1 + 5,6х2 +7,2х3 ≤ 240.
Данная математическая модель выглядит следующим образом:
Z(X) = 90х1+140х2+200х3 max
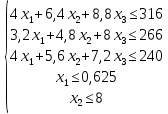
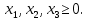
Приведем задачу линейного программирования к каноническому виду:
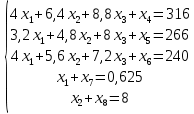
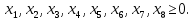
Далее, стандартная форма записи допустимого базисного решения будет иметь следующий вид:
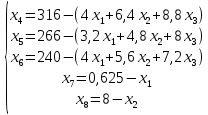
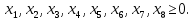
Следовательно: Z1(X) = 0-(90х1+140х2+200х3) min
Данному базисному решению соответствует следующая симплекс-таблица:
| | Своб. член | х1 | х2 | х3 |
| Z1 | 0 | 90 | 140 | 200 |
| х4 | 316 | 4 | 6,4 | 8,8 |
| х5 | 266 | 3,2 | 4,8 | 8 |
| х6 | 240 | 4 | 5,6 | 7,2 |
| х7 | 0,625 | 1 | 0 | 0 |
| х8 | 8 | 0 | 1 | 0 |
Нашли генеральный элемент – 8, так как в строке Z выбираем положительное число (у нас число 200 – выбираем столбец х3), а в столбце х3, не считая строки Z, выбираем то значение, для которого отношение к нему свободного члена минимально (266/8 – минимальное значение). В новом допустимом базисном решении х3 и х5 изменим на противоположные. Найдем это решение, перейдя к новой симплекс-таблице:
| | Своб. член | х1 | х2 | х5 |
| Z1 | -6650 | 10 | 20 | -25 |
| х4 | 23,4 | 0,48 | 1,12 | -1,1 |
| х3 | 33,25 | 0,4 | 0,6 | 0,125 |
| х6 | 0,6 | 1,12 | 1,28 | -0,9 |
| х7 | 0,625 | 1 | 0 | 0 |
| х8 | 8 | 0 | 1 | 0 |
Определяем генеральный элемент в новой таблице – 1,28. В новом допустимом базисном решении х2 и х6 изменим на противоположные. Найдем это решение, перейдя к новой симплекс-таблице:
| | Своб. член | х1 | х6 | х5 |
| Z1 | -6659,375 | -7,5 | -15,625 | -10,9375 |
| х4 | 22,875 | | -0,875 | |
| х3 | 32,96875 | | -0,46875 | |
| х2 | 0,46875 | 0,875 | 0,78125 | -0,70313 |
| х7 | 0,625 | | 0 | |
| х8 | 7,53125 | | -0,78125 | |
Далее генеральный столбец выбрать нельзя. Значит, оптимальное решение имеет вид Хопт=(0; 0,46875; 32,96875; 22,875; 0; 0; 0,625; 7,53125), Zmin=-6659,375.
Xmax=(0; 0,46875; 32,96875)
Zmax=6659,375.
Так как в условии задачи указано, что спрос на шайбы не превосходит 0,625т, а спрос на гайки не превышает 8т, то мы полностью удовлетворяем условие задачи.
Вывод: при объеме выпуска 0 тонн шайб, 0,46875 тонн гаек и 32,96875 тонн болтов максимальная прибыль от реализации крепежных изделий составит 6659,375 у.е.
б) с использованием надстройки «Поиск решения» MSExcel.
Построив математическую модель, можно перейти к построению табличной модели. Для этого введем данные – параметры, которые характеризуют выпуск крепежных изделий, в единую таблицу.

В колонке «Запас ресурса» указаны ограниченные месячные запасы ресурсов, которыми располагает предприятие. Целевая функция. В ячейке В11 будет отображаться значение целевой функции. Формула, по которой это значение будет рассчитано, определяется выражением: