90х₁+140х₂+200х₃

Используя обозначения соответствующих ячеек в Excel, получим следующее:

=СУММПРОИЗВ(B10:D10;B7:D7)

Ограничения задачи представляют собой сумму произведений каждой из ячеек переменных (B10, D10) на соответствующую ячейку для коэффициентов конкретного ограничения (B7, D7).

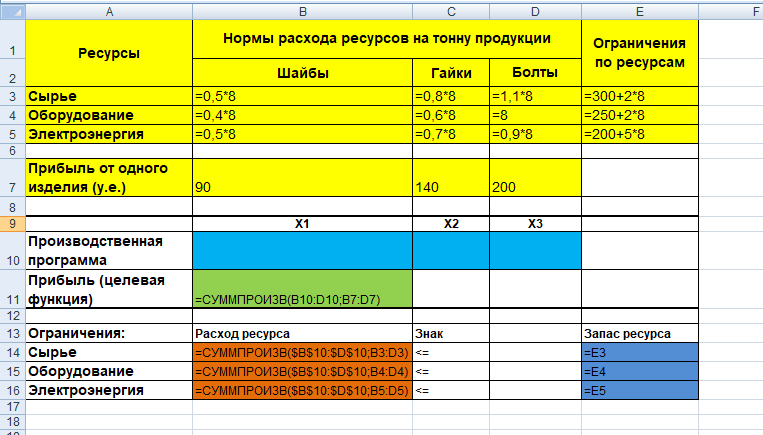
Таким образом, для первого ограничения в ячейку В14 будет введена формула:

=СУММПРОИЗВ($B$10:$D$10;B3:D3),

где символ $ означает, что при копировании этой формулы в другие места листа Excel номер строки 10 не изменится. Скопируем эту формулу в ячейки В15 и В16. В формуле будет меняться только номер строки во втором массиве. Этот номер является строкой, где записано ограничение.



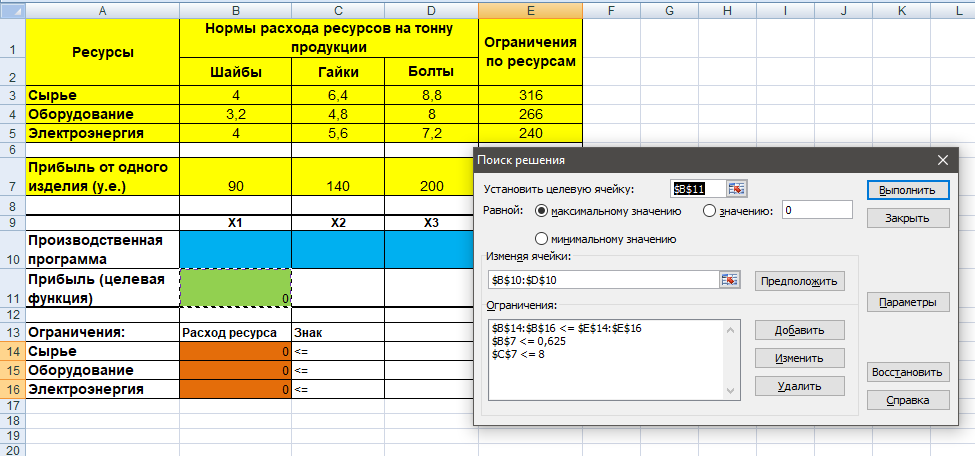
С помощью «Поиска решения» найдем решение данной задачи. В диалоговом окне «Поиска решения» требуется ввести необходимые параметры.



Результаты поиска решения следующие:



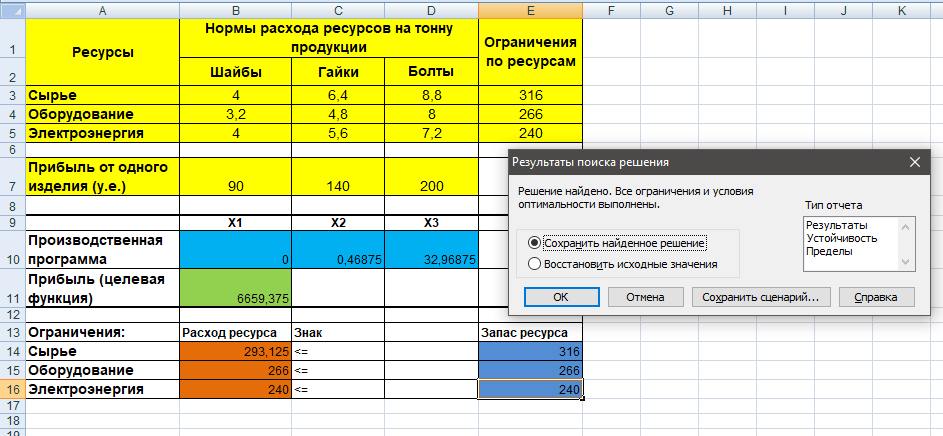
Вывод: при объеме выпуска 0 тонн шайб, 0,46875 тонн гаек и 32,96875 тонн болтов максимальная прибыль от реализации крепежных изделий составит 6659,375 у.е.

ЗАКЛЮЧЕНИЕ
В курсовой работе рассмотрены варианты решений оптимизационных экономических задач методами линейного программирования.

Метод математического программирования является основным инструментом описания оптимальных решений. Оптимальным решением считается такой способ действия, который в наибольшей степени способствует достижению поставленной в задаче цели. Наиболее простыми и лучше всего изученными среди задач математического программирования являются задачи линейного программирования, изучающие методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием.

В настоящее время линейное программирование является одним из наиболее употребительных аппаратов математической теории оптимального принятия решения. Для решения задач линейного программирования разработано сложное программное обеспечение, дающее возможность эффективно и надежно решать практические задачи больших объемов. Эти программы и системы снабжены развитыми системами подготовки исходных данных, средствами их анализа и представления полученных результатов.

---

Современные методы линейного программирования достаточно надежно решают задачи общего вида с несколькими тысячами ограничений и десятками тысяч переменных. Для решения сверхбольших задач используются уже, как правило, специализированные методы.

В результате выполнения работы можно сделать следующие выводы:

- сформированы математические модели задач;

- получены решения задач с помощью надстройки «Поиск решения» табличного процессора Excel;

- анализ решения показал, что ресурс электроэнергия является недефицитными, поэтому при расширении производства следует начинать с сокращения запасов электроэнергии;

- анализ ввода в производство нового ограничения продукции показал, что данное ограничение не изменит доход предприятия.

В данной курсовой работе были рассмотрены и решены основные задачи линейного программирования: задачи оптимизации производства, задача составления смеси и составления расписания. Для решения данных задач были применены методы линейного программирования, а именно: графический метод и симплекс-метод, а так же использовалась надстройка Microsoft Excel «Поиск решения».

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Ишханян М.В., Фроловичев А.И. Методы оптимальных решений: учебное пособие. – М.: МИИТ, 2015. – 132 с.

2. Фроловичев А.И. Конспект лекций по дисциплине «Методы оптимальных решений» 2021/2022 учебный год. 

---

Смотрите также файлы

• Тесты тут httpst mehelp synergy По назначению и характеру использования информационные технологии.pdf

• Состав, структура и динамика основных средств ооо "жкх холмогоры".doc

• Применение радиоактивных изотопов в сельском хозяйстве.docx

• Вопросы к экзамену Роль экономического анализа в управлении и последовательность его проведения.docx

• Срок прохождения практики с 20 г по 20 г.docx