Файл: Правительство Российской Федерации.docx

Скачать файл (0,20Мб)

Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 07.11.2023

Просмотров: 100

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Правительство Российской Федерации

Пермский филиал федерального государственного автономного образовательного учреждения высшего профессионального образования

«Национальный исследовательский университет
«Высшая школа экономики»

Финансовый менеджмент

(основы финансовых расчетов)

к.э.н., доцент департамента

экономики и финансов

Жукова Наталья Юрьевна
Zhukovanu08@mail.ru

2022

ВВЕДЕНИЕ
Рассмотрим два инвестиционных проекта А и В, которые генерируют потоки денежных средств начиная с конца первого года и окончанием в конце четвертого года (издержки на реализацию проектов одинаковы, выплачиваются в текущий момент). Какой из проектов более предпочтителен?

год	Проект А	Проект В
1	500	900
2	600	600
3	700	500
4	800	400

Условные обозначения:

проценты за весь срок ссуды (interest);
первоначальная сумма долга или современная (текущая) стоимость (present value);
ставка процентов за период (interest rate);

наращенная сумма или будущая стоимость (future value), т.е. первоначальная сумма долга с начисленными на нее процентами к концу срока ссуды;

срок ссуды в годах.

Простые проценты

Задачи на формулу простых процентов на практике встречаются редко, поскольку к этим задачам прибегают в случаях:

выдачи краткосрочных ссуд, т.е. ссуд, срок которых либо равен году, либо меньше его, с однократным начисление процентов;

когда проценты не присоединяются к сумме долга, а периодически выплачиваются.

Задача 1

Вкладчик положил в банк, выплачивающий 5% годовых простых по депозитам сумму 1500 рублей. Какая сумма будет на счету у вкладчика а) через 3 года, б) через 5 лет и 3 месяца, если начисляются простые проценты.

Задача 2

а) Какую сумму надо положить в банк, выплачивающий 6% простых в год, чтобы через 2 года 6 месяцев получить 10000 рублей?

б) Какую сумму надо положить в банк, чтобы через 10 лет купить квартиру стоимостью 2800000 рублей, если по вкладам банк выплачивает 9% простых годовых?

Задача 3

В банк положили 1500 рублей, через 1 год и 3 месяца на счету было 1631,25. Сколько % простых выплачивает банк в год?

Задача 4

Г-н Иванов занял у г-на Петрова деньги, получив от него 9800 и выдав вексель, по которому обязался выплатить 10000 рублей через 3 месяца. Под какой простой годовой процент выдан этот вексель?

Векселем называется безусловное письменное обязательство векселедателя (заемщика) выплатить векселедержателю (кредитору) в указанное время и в указанном месте указанную сумму (номинальную стоимость векселя).

Задача 5

Сколько времени необходимо для того, чтобы получить из 1000 рублей 1200 рублей на депозитном счете, если банк начисляет 8% простых в год?

Задача (самостоятельно)

Можно приобрести машину за 5 тыс.долларов наличными или заплатив 5,4 тыс.долларов через год. Если у покупателя на счету в банке не менее 5 тыс.долларов, и банк платит 7% простых годовых, то какой вариант приобретения автомобиля предпочтительнее?

Потребительский кредит

Потребительским кредитом называется ссуда размером PVс годовой процентной ставкой r, предоставленная на срокn (в годах) и предусматривающая погашение долговой суммы (с учетом процентных денег) при помощи l одинаковых платежей, осуществляемых через равные периоды времени, причем в случае простых процентов размер каждого погашающего платежа равен

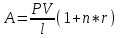Задача 6

Покупатель приобрел холодильник, цена которого 20000 руб. в кредит, уплатив сразу 5000 руб. и обязавшись уплатить остальное в течение 6 месяцев, делая ежемесячные равные платежи. Какую сумму он должен выплачивать ежемесячно, если продавец требует за кредит 6% простых в год?

Простой дисконт

Финансовая сделка, когда проценты с наращенной суммы удерживаются непосредственно при выдаче ссуды. Процесс начисления и удержания процентов вперед, до наступления срока погашения долга, называют учетом, а сами проценты в виде разности наращенной и первоначальной сумм долга дисконтом (discount).

Задача 7

Финансовая компания дает ссуду 5000 рублей на 3 года под простой дисконт, равный 5% в год. Какую сумму получит клиент в момент получения ссуды?

Задача 8

Г-н Сидоров желает получить ссуду 10000 (на руки) на 3 месяца. Сколько он должен вернуть через 3 месяца, если возьмет ссуду под 8% простого дисконта?

Задача 9

Сколько должен вернуть Сидоров, если он возьмет ссуду 10000 под 8% простых годовых на тот же срок?

Банковский учет

Операция учета (учет векселей) заключается в том, что банк или другое финансовое учреждение до наступления платежа по векселю покупает его у предъявителя по цене ниже суммы векселя, т.е. приобретает его с дисконтом. Сумма, которую получает векселедержатель при досрочном учете векселя, называется дисконтированной величиной векселя. При этом банк удерживает в свою пользу проценты (дисконт) от суммы векселя за время, оставшееся до срока его погашения.
Учетом (дисконтированием) векселя называется его покупка по цене, меньшей номинальной стоимости.
Дисконтом называется разница между номинальной стоимостью векселя и ценой его покупки.
Для расчета дисконта используется учетная ставка (простая учетная ставка):

D = FV - PV = FV * n* d = FV *t / T *d ,

где n – продолжительность срока в годах от момента учета до даты выплаты известной суммы в будущем.

Отсюда:

PV = FV - FV * n * d = FV *(1 - n *d).

Очевидно, что чем выше значение учетной ставки, тем больше дисконт. Дисконтирование по простой учетной ставке чаще всего производится по французской практике начисления процентов, т.е. когда временная база принимается за 360 дней, а число дней в периоде берется точным.

Задача 10

Тратта (переводной вексель) выдана на 10000 рублей с уплатой 14 октября 2014 г. владелец векселя учел его в банке 15 августа по учетной ставке 10%. Сколько он получил? Какую сумму он получит, если срок уплаты по векселю 14 октября 2015 года?

Переменные ставки
Ставка процентов не является застывшей на вечные времена величиной, поэтому в финансовых операциях предусматривают дискретно изменяющиеся во времени процентные ставки. Пусть на интервалах начисления (в годах) n₁, n₂, …, n_kприменяются простые процентные ставки r₁, r₂, …, r_k соответственно. Тогда наращенную сумму определяют по формуле:

FV= PV*(1+n₁*r₁+ n₂*r₂+…+ n_k*r_k) =

.

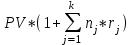Пример . Вклад в размере 3000 руб. был положен в банк. В первой половине года применялась простая процентная ставка r₁ = 15 % годовых, вовторой половине года –

r₂ = 12 % годовых. Определить наращенную сумму.
Решение.

При наращении простых процентов процентные деньги растут в арифметической прогрессии. Графически это показано на рис. 1, где Р – начальная сумма, отрезки Р_кТ_к – наращенные суммы и отрезки Р_кМ_к – процентные деньги.

Рис. 1. Наращение простых процентов

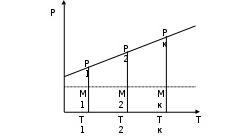
Модификация формулы:

,

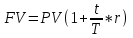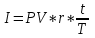где t – число дней ссуды, т.е. продолжительность срока на который выдана ссуда;

T – расчетное число дней в году (временная база).
Различные способы рассмотрения срока ссуды:

с приближенным числом дней ссуды, это способ называется немецким и часто упоминается как способ 360/360. Число Т – продолжительность года условно принимают за 360 дней, целого месяца – за 30 дней, поэтому число t состоит из полного числа месяцев плюс точное число дней в оставшемся неполном месяце минус один день (день выдачи и день погашения ссуды считаются одним днем). Этот способ обычно используется в Германии, Дании, Швеции.
с точным числом дней ссуды, или «французская практика расчета», когда продолжительность года условно принимается за 360 дней, а продолжительность ссуды рассчитывается точно по календарю минус один день (день выдачи и день погашения считаются одним днем). Этот способ имеет распространение во Франции, Бельгии, Испании, Швеции и обозначается АСТ/360.
точные проценты с точным числом дней ссуды, или «английская практика» (которая обозначается АСТ/АСТ), когда продолжительность года и продолжительность ссуды берутся точно по календарю (минус 1 день).

Для упрощения процедуры расчета точного числа дней финансовой операции пользуются специальными таблицами порядковых номеров дней года, в которых все дни в году последовательно пронумерованы. Точное количество дней получается путем вычитания номера первого дня финансовой операции из номера последнего дня финансовой операции.

Сложные проценты

Способы начисления процентов

Задача 1

Банк начисляет ежегодно 8% сложных. Клиент положил в этот банк 20000. Какая сумма будет на счету:

А) через 5 лет Б) через 6 лет и 3 месяца

Задача 2

Банк начисляет ежегодно 12% сложных. Клиент положил в этот банк 20000. Какая сумма будет на счету через 5 лет при начислении процентов а) 1 раз в квартал, б) ежемесячном начислении?

Задача 3

Г-н Смирнов может вложить деньги в банк, выплачивающий j

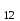=24%. Какую сумму ему следует вложить, чтобы получить через 2 года и 6 месяцев 3000 рублей?
Задача 4

Г-н Филиппов хочет вложить 5000 рублей, чтобы через 2 года получить 7000 рублей. Под какую процентную ставку он должен вложить свои деньги?

Задача 5

Определить годовую ставку начисляемых ежегодно процентов, если вложенная сумма денег удваивается через 8 лет.

Задача 6

За какой срок первоначальный капитал в 50000 руб. увеличится до 200000 руб., если: а)начисляются 20% годовых сложных; б)проценты начисляются ежеквартально?

Задача 7

Условия как в задаче 10 по теме 1.

Вексель выдан на 10000 рублей с уплатой 14 октября этого года. Банк учел 15 августа по сложной учетной ставке 10%. За сколько купил вексель банк у владельца? Сколько получит владелец векселя, если срок погашения по векселю 14 октября следующего года?

Сравнение силы роста простых и сложных процентов представлены на рис. 3.

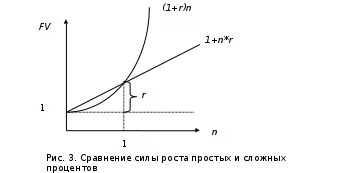
Как видно из рис.2, при кратковременных ссудах начисление по простым процентам предпочтительнее, чем по сложным процентам, при сроке в один год разница отсутствует, но при среднесрочных и долгосрочных ссудах наращенная сумма значительно выше рассчитанная по сложным процентам, чем по простым.

Таким образом, для лиц, предоставляющих кредит:

более выгодна схема простых процентов, если срок ссуды менее года (проценты начисляются однократно в конце года);
более выгодной является схема сложных процентов, если срок ссуды превышает год;
обе схемы дают одинаковый результат при продолжительности периода один год и однократном начислении процентов.

Достаточно часто в финансовых контрактах при предоставлении кредитов на срок, меньший 1 года, расчеты, как правило, по схеме простых процентов. При предоставлении кредитов на срок, больший 1 года, возможны три случая: