ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 90
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Контрольные вопросы
-
Понятие «влажный воздух». Особенности изменения состояния влажного воздуха в отличие от идеальной газовой смеси. -
Состояние водяных паров во влажном воздухе. -
Понятие о температуре точки росы. Методика определения tросы по Hd-диаграмме. -
Основные характеристики влажного воздуха. Определение d,
, H, pn и pв. -
Устройство, принцип действия и назначение психрометра. -
Hd-диаграмма влажного воздуха. Графическое представление процессов нагревания и сушки влажным воздухом. -
Методика расчета количества теплоты, затраченной на нагревание воздуха. Цель нагревания. -
Методика расчета массы вещества, отводимой от высушиваемого материала в процессе сушки. -
Понятие о погрешностях измерения, источники погрешностей. Методика расчета систематических погрешностей измерения температур воздуха на входе в установку и на входе из неё.
| | Приложение |
| Психрометрическая таблица влажного воздуха |  |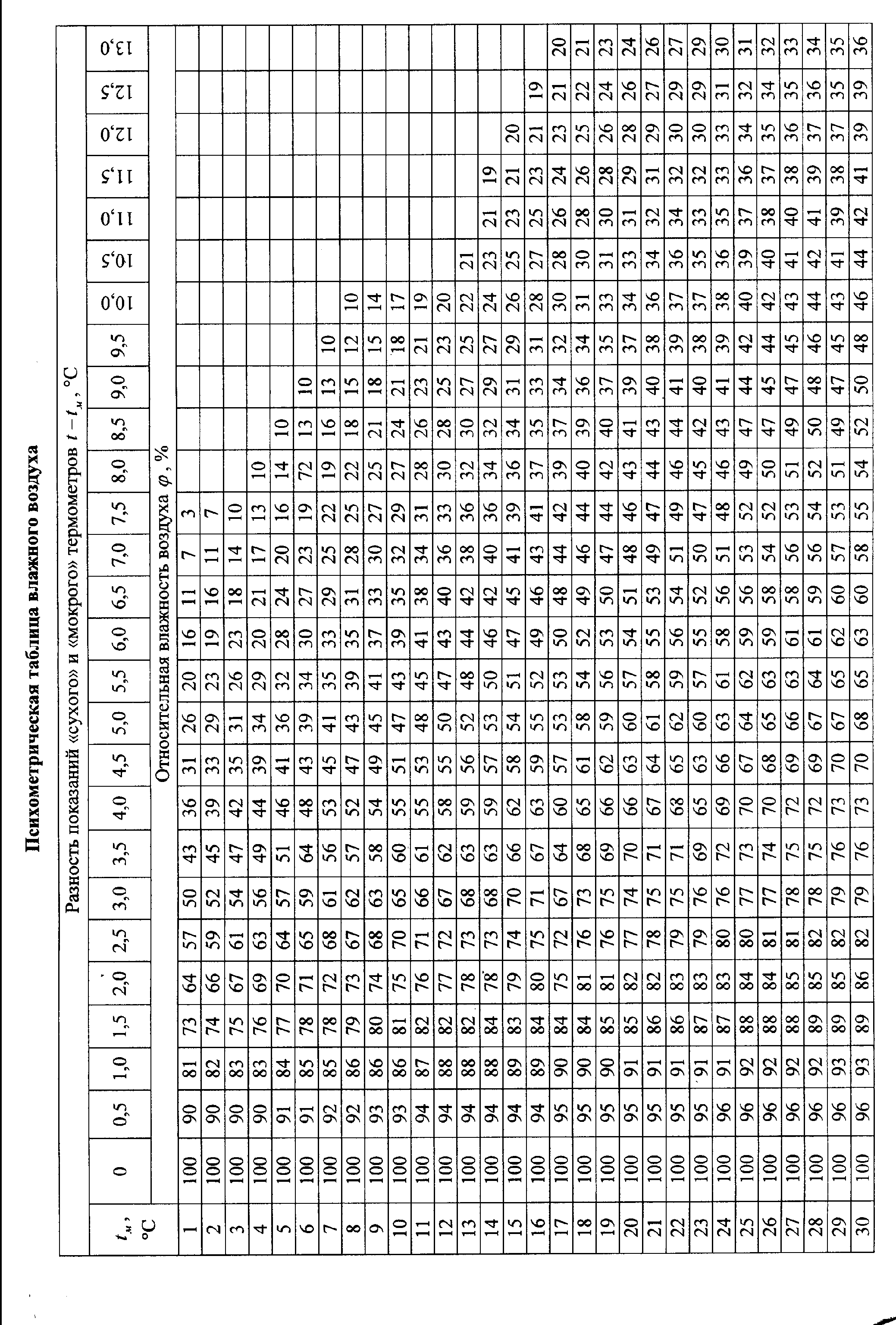
Лабораторная работа № 22
Измерение теплоемкости воздуха
Цель работы: Ознакомиться с понятием теплоемкости вещества, освоить технику измерения теплоемкости воздуха методом проточного калориметрирования.
Задание
-
Провести опыты по определению удельной изобарной теплоемкости воздуха при тепловом режиме, указанном преподавателем. -
Рассчитать средние значения теплоемкостей Cpm и Cvm, изменения внутренней энергии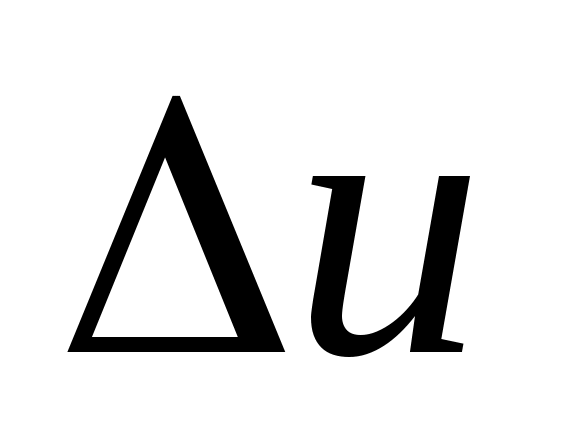
, энтальпии 
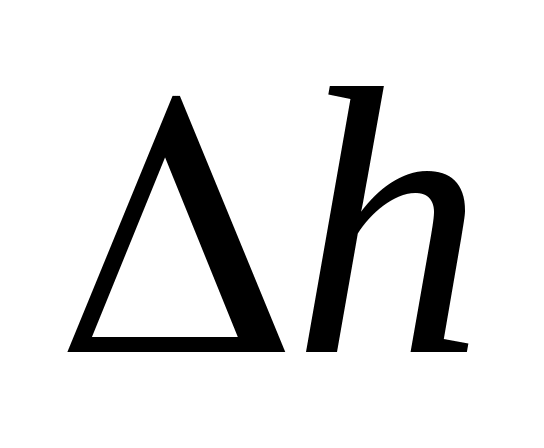и энтропии 
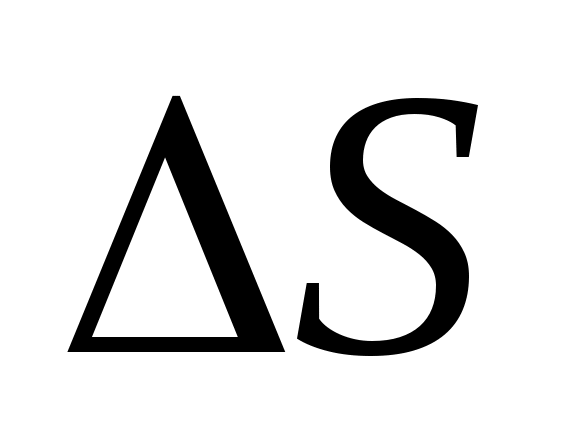, а также показатель адиабаты воздуха k в условиях опыта. -
Составить отчет о выполненной работе, который должен содержать: задание, основы теории (кратко), схему экспери-ментальной установки, таблицу опытных данных, обработку опытных данных и результаты опытов в виде таблицы.
Основы теории
При проведении расчетов процессов и аппаратов химической технологии часто приходится определять количество подведенной или отведенной теплоты. Наиболее просто это сделать, используя теплоемкость теплоносителей.
Удельной теплоемкостью называется количество теплоты, которое необходимо подвести к единице количества вещества, чтобы изменить его температуру на 1 градус. В связи с этим определением различают:
-
удельную массовую теплоемкость
, 
, откуда 
, кДж; (1)-
удельную объемную теплоемкость
, 
, откуда 
, кДж; (2)-
удельную мольную теплоемкость
, 
, откуда 
, кДж, (3)где m – масса газа, кг;
Vн.у., нм3 – объем газа, приведенный к нормальным условиям (
, Рн=760 мм рт. ст.=1,013105 Па, Тн=273 К);L – число киломолей вещества (
), кмоль;
молекулярная масса газа, кг/кмоль;х – индекс, указывающий характер процесса подвода теплоты Qx, например, при
(Qp), при 
(Qv).Поэтому различают:
Ср – изобарная теплоемкость,
Сv – изохорная теплоемкость.
Эти теплоемкости для идеальных газов связаны уравнением Майера:
. (4)С=f(t)-нелинейная
СХ=a+bt+et2+…
а
С
Т
СХ=const в
б
С=f(t)-линейная
СХ=a+bt
t
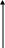
Рис.1. Зависимость теплоемкости от температуры
еплоемкость зависит от температуры в общем случае нелинейно (рис. 1 а). При определении количества теплоты для нагревания при
от t1 до t2 обычно применяют средние теплоемкости 
(здесь индекс «m» означает «средний»!), которые при нелинейной зависимости рассчитываются по средним табличным значениям теплоемкостей 
в интервале температур от 0 до t:
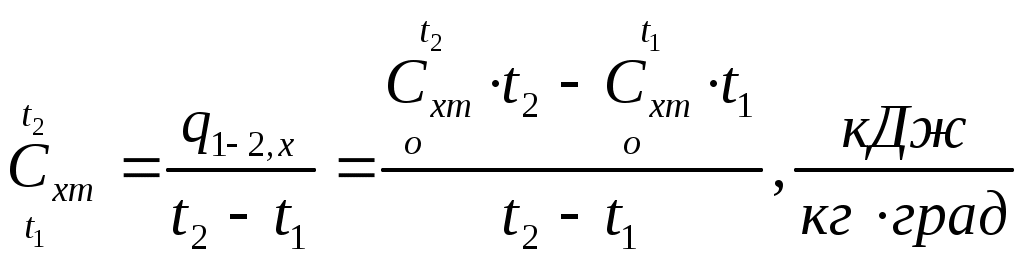, (5)где
удельная массовая теплота, кДж/кг.Следовательно
, (6)
, (7)т.е. наиболее точно теплоту можно подсчитать как по значениям теплоемкостей, так и по значениям энтальпий h (при
) и внутренних энергий u (при 
). Значения 
, u и h приводятся в справочной литературе в виде таблиц /2/.В пределе при уменьшении интервала температур в выражении (5) получим теплоемкость при заданной температуре
t, называемую истинной теплоемкостью, Сх,ист.
. (8)Со средней теплоемкостью она связана соотношением
, 
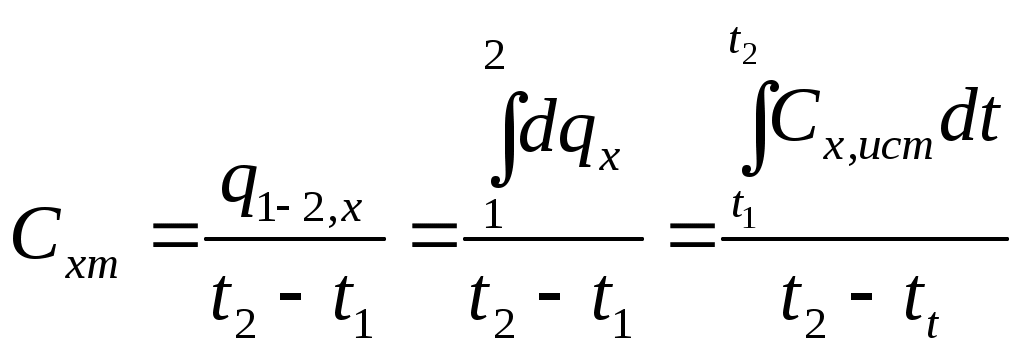. (9)Для приближенных расчетов можно учесть линейную зависимость теплоемкости от температуры (рис. 1б):
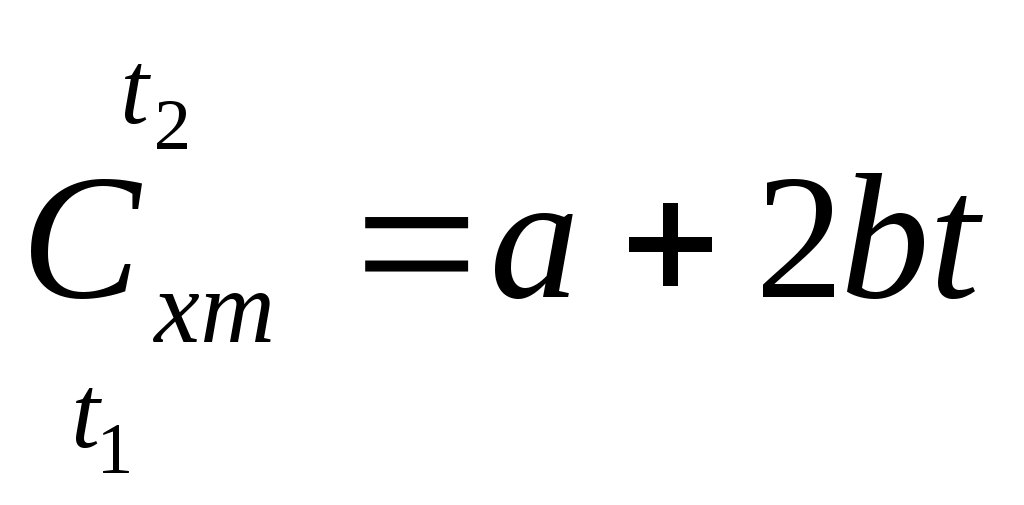, (10)где a и b – индивидуальные коэффициенты (из таблиц /2/),
.В соответствии с молекулярно-кинетической теорией внутренняя энергия газов распределяется равномерно по степеням свободы i поступательного и вращательного движения молекул. Для одноатомной молекулы i=3 степеням свободы поступательного движения, т.е. изменяется положение молекулы в координатах x, y и z. Для двухатомных молекул к трем степеням свободы поступательного движения добавляются две степени свободы вращательного движения i = 3+2 = 5. С некоторой корректировкой для трех- и многоатомных газов число степеней свободы принимается равным i= 7.
Для идеальных газов при не очень высоких температурах на каждую степень свободы при
расходуется энергия 
кДж/(кмольград). Поэтому постоянные (рис.1, в) мольные теплоемкости 
можно определить по числам степеней свободы i, а 
по (i + 2) из таблицы 1.Таблица 1
| Атомность газов | , кДж/(кмольград) |  ,кДж/(кмольград) |
| 1 атомные |  |  |
| 2 атомные |  |  |
| 3 и многоатомные |  |  |
Для пересчета различных удельных теплоемкостей удобны соотношения:
, 
; 
, 
;
, , (11)где
удельный объем 1 кмоля газа при нормальных условиях, 
.Измерение теплоемкости Срт воздуха
методом проточного калориметрирования
В лабораторном калориметре (рис. 2) к потоку газа подводится теплота от электронагревателя и измеряются все величины, необходимые для расчета теплоемкости: расход газа, количество подведенной теплоты, температуры газа на входе в калориметр и на выходе из него.
Расчетное уравнение для определения теплоемкости Срт в таком калориметре может быть получено следующим образом. Запишем уравнение первого закона термодинамики для стационарного потока газа для сечения 1 на входе и 2 на выходе:
, (12)где
тепловой поток – количество теплоты, подведенной от электронагревателя в единицу времени, Дж/с или Вт;
массовый расход газа, кг/с;h – энтальпия газа, Дж/кг;
W – скорость газа, м/с;
g – ускорение свободного падения, м/с2;
y – координата сечений 1 и 2 канала по высоте, м.
В данном случае работой, затрачиваемой на изменение кинетической энергии газа
