ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 91
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, можно пренебречь, так как скорости газа W1 и W2 мало отличаются друг от друга. Работа, затрачиваемая на изменение потенциальной энергии 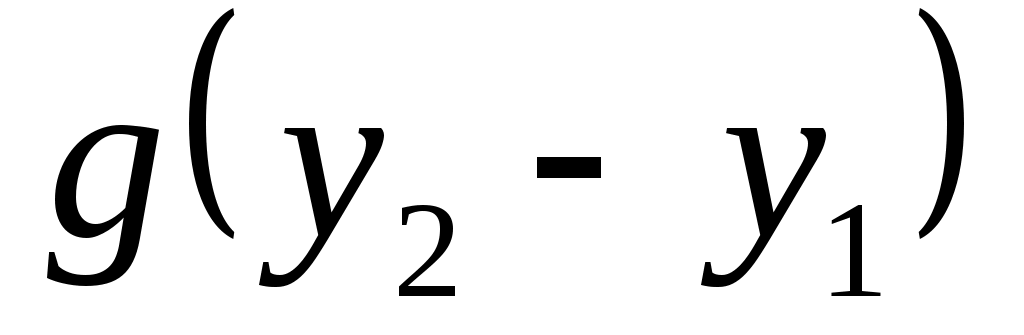 , равна нулю, поскольку калориметр расположен горизонтально
, равна нулю, поскольку калориметр расположен горизонтально 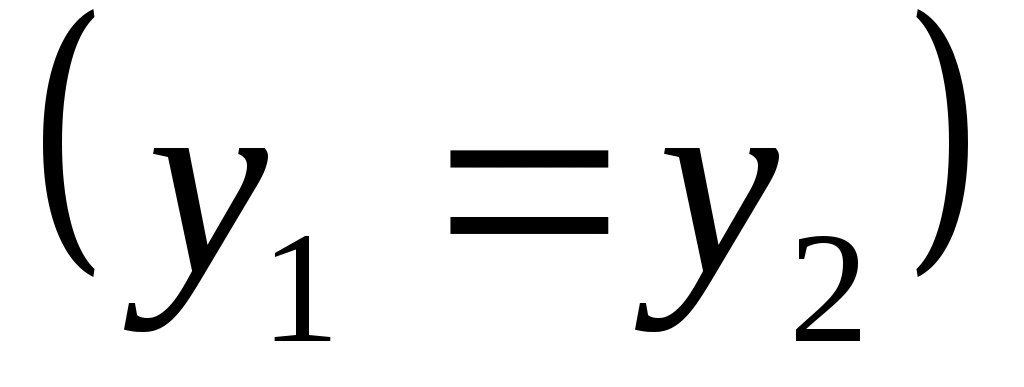 .
.
Таким образом, уравнение (12) принимает вид:
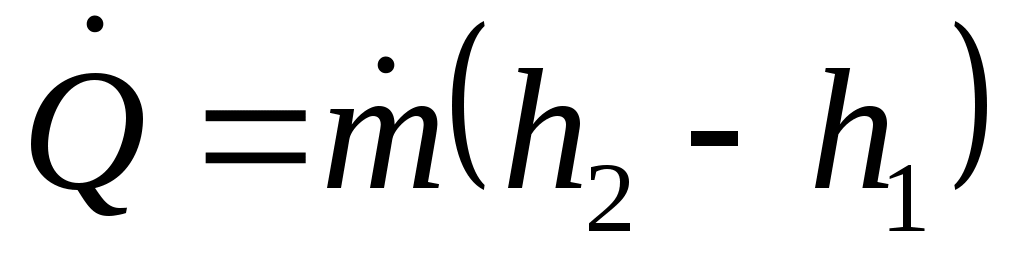 . (13)
. (13)
Проинтегрировав известное выражение для идеального газа
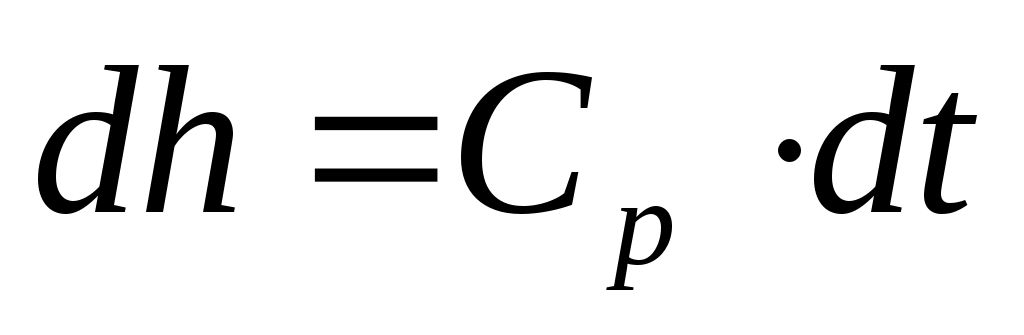 (14)
(14)
в интервале температур от t1 до t2, получим:
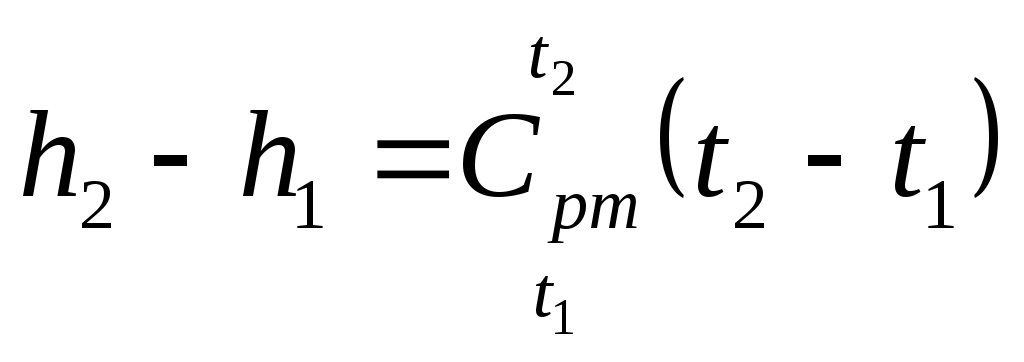 , (15)
, (15)
где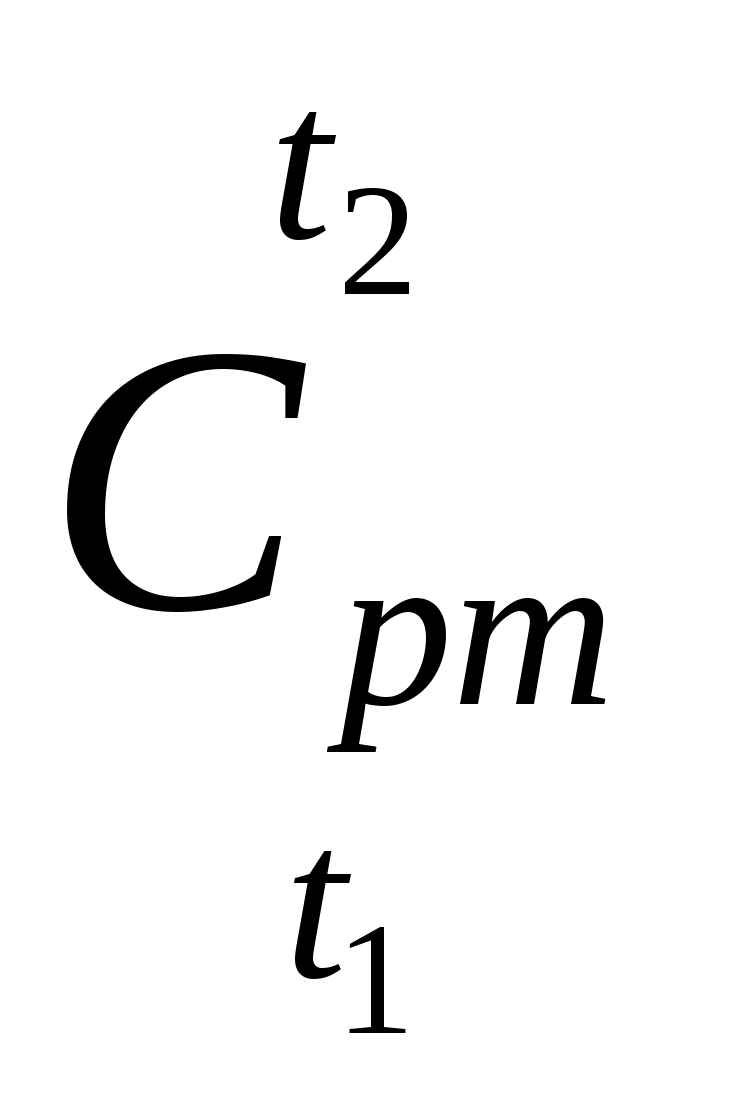 средняя теплоемкость при
средняя теплоемкость при  в интервале температур от t1 до t2.
в интервале температур от t1 до t2.
Из уравнений (13) и (15) следует:
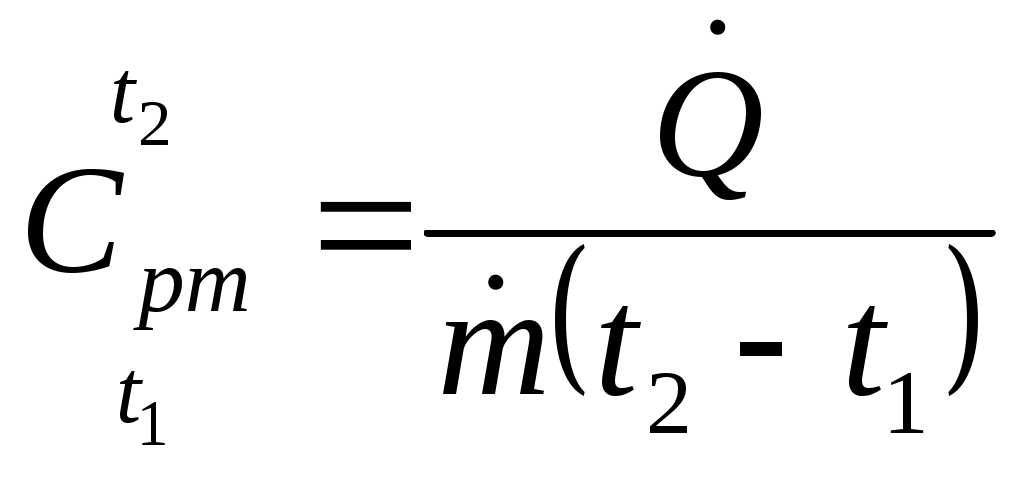 . (16)
. (16)
Проведение опытов
Рис.2. Схема экспериментальной установки:
1 – проточный калориметр, изготовленный из стекла; 2 – вакууммированная оболочка, предназначенная для уменьшения потерь тепла в окружающую среду; 3 – электронагреватель; 4 – дифференциальная термопара, 5,8 – лабораторные автотрансформаторы; 6 – стабилизатор напряжения; 7 – переключатель; 9 – милливольтметр; 10 – вольтметр; 11 – амперметр; 12 – вентилятор; 13 – ротаметр.
Н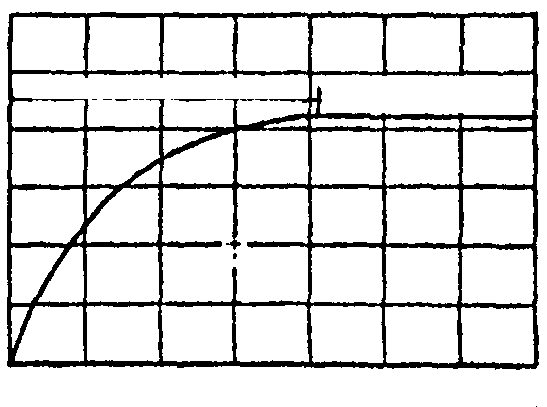 а графике стационарности (рис. 3) через каждые 2 мин наносить показания милливольтметра е, мВ до наступления стационарного режима.
а графике стационарности (рис. 3) через каждые 2 мин наносить показания милливольтметра е, мВ до наступления стационарного режима.
Таблица 2
где Прот. – показания ротаметра; объемный расход – определяется по градуировочному графику; I – сила тока в электронагревателе – показания амперметра; Uэл –падение напряжения на электронагревателе – измеряется с помощью вольтметра; е – термо-э.д.с. – показания милливольтметра;
объемный расход – определяется по градуировочному графику; I – сила тока в электронагревателе – показания амперметра; Uэл –падение напряжения на электронагревателе – измеряется с помощью вольтметра; е – термо-э.д.с. – показания милливольтметра;  изменение температуры газа в калориметре – определяется по градуировочному графику; В – барометрическое давление, р – давление газа, равное атмосферному, т.е. барометрическому давлению, р=В.
изменение температуры газа в калориметре – определяется по градуировочному графику; В – барометрическое давление, р – давление газа, равное атмосферному, т.е. барометрическому давлению, р=В.
Обработка опытных данных
Таблица 3
Вычислить расхождения с экспериментальными данными
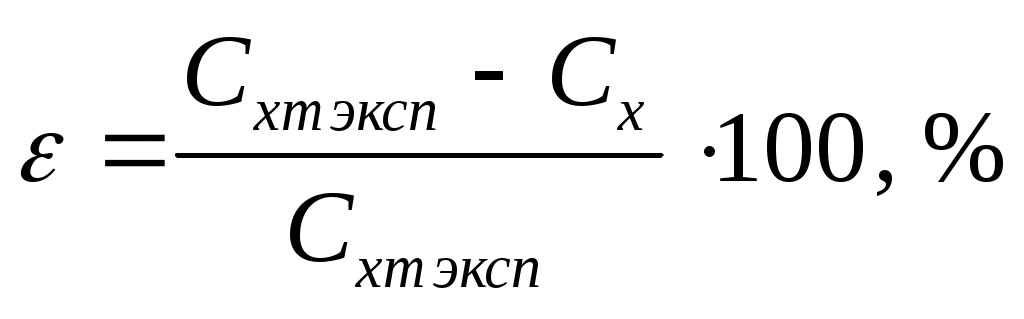 .
.
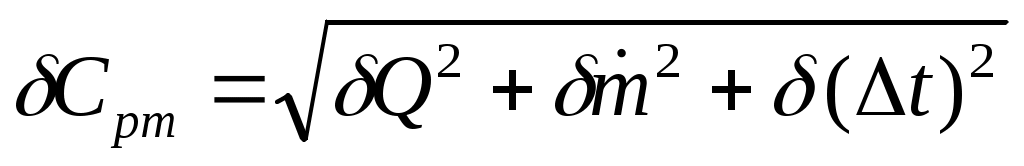 .
.
Подробно материал к этому пункту изложен в разделе «Оценка погрешности эксперимента».
Контрольные вопросы
Лабораторная работа № 23
Исследование pv-диаграммы углекислого газа.
Опыт Эндрюса
Цель работы: ознакомиться с общими свойствами идеальных и реальных газов; освоить методику экспериментального определения зависимости p-v-t реальных газов.
Задание.
Основы теории
Идеальным газом называется воображаемый газ, молекулы которого представляют собой материальные точки, не имеющие собственного объема и не взаимодействующие между собой. Зависимость между основными термодинамическими параметрами такого газа определяется уравнением состояния идеального газа – уравнением Клапейрона-Менделеева:
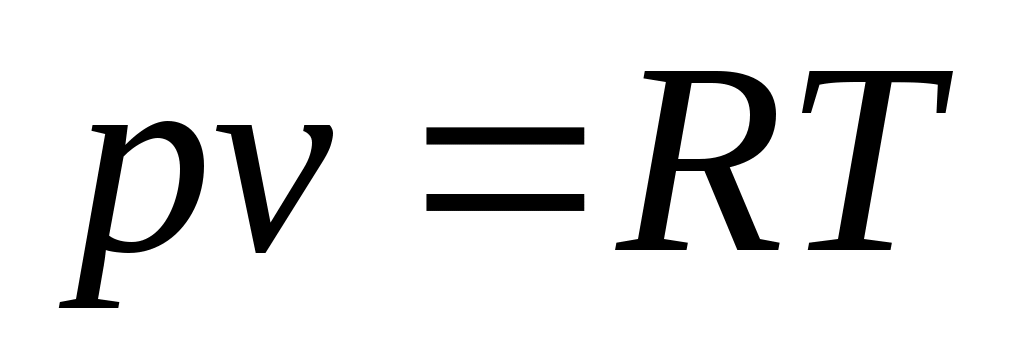 , (1)
, (1)
где
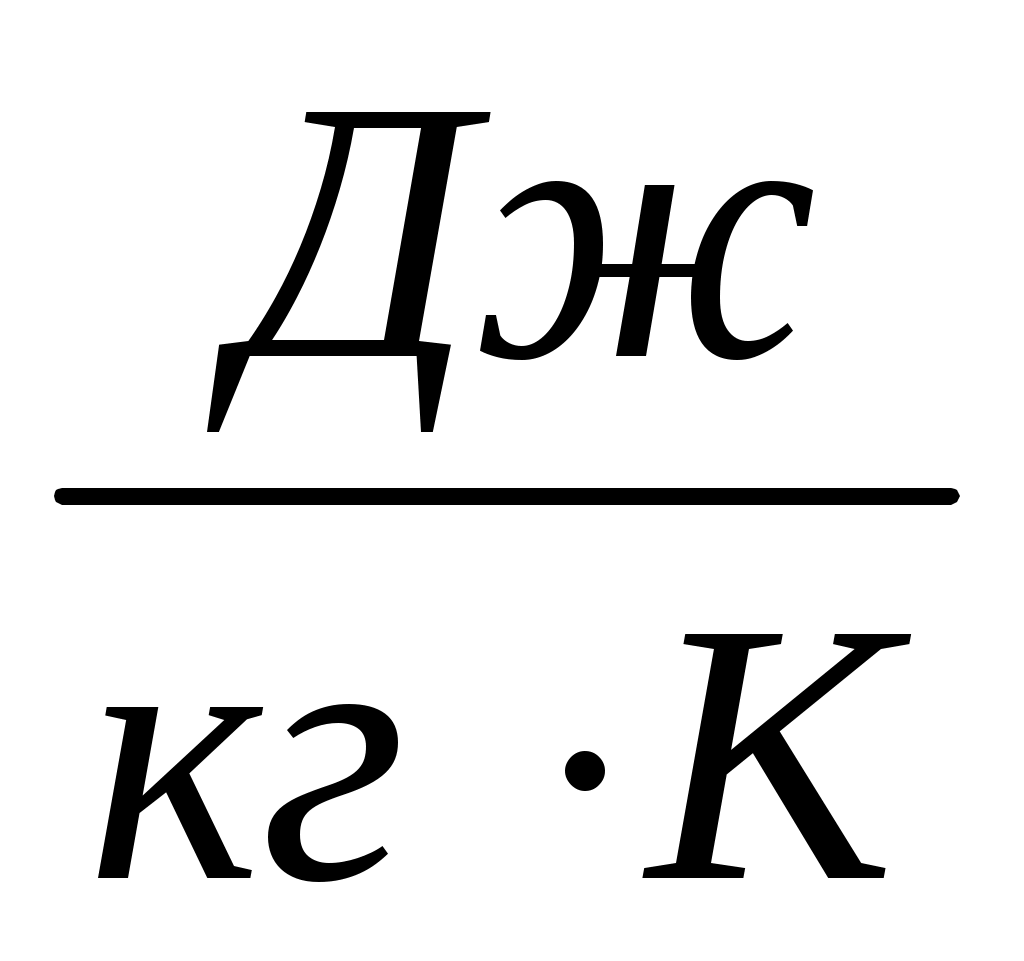 газовая постоянная;
газовая постоянная;
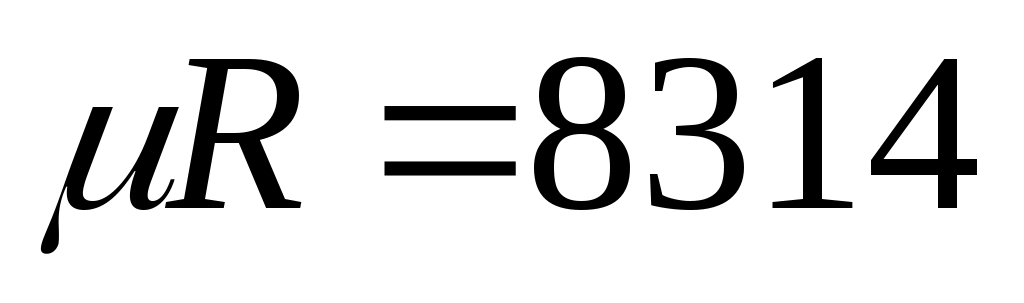
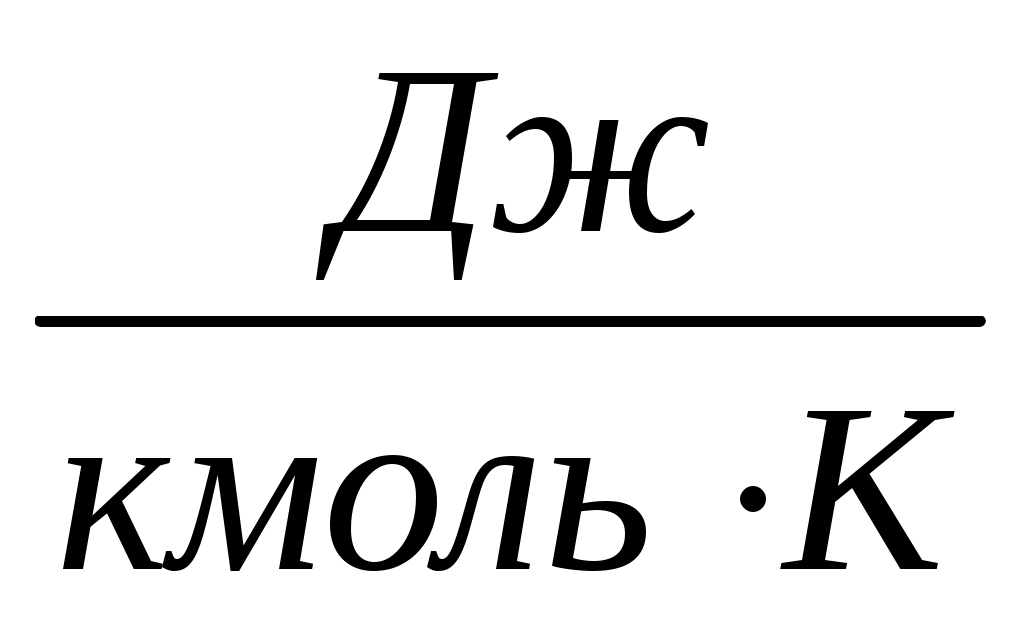 универсальная газовая постоянная.
универсальная газовая постоянная.
Реальные газы состоят из молекул, имеющих конечный собственный объем, между которыми действуют силы межмолекулярного взаимодействия (силы притяжения и отталкивания). Эти газы описываются уравнением (1) только при малых плотностях, когда среднее расстояние между центрами молекул сравнительно велико, и эти силы не проявляются. В более плотных реальных газах со значительно меньшим расстоянием между молекулами необходимо учитывать и эти силы, и собственный объем молекул. Поведение реальных газов качественно отражает уравнение Ван-дер-Ваальса:
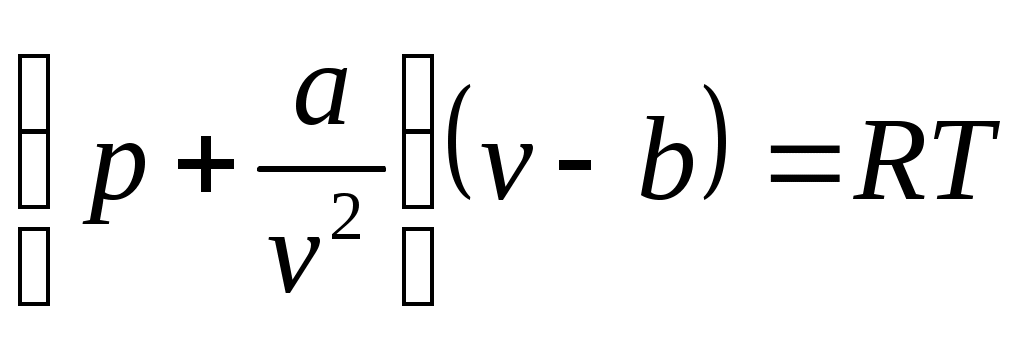 , (2)
, (2)
где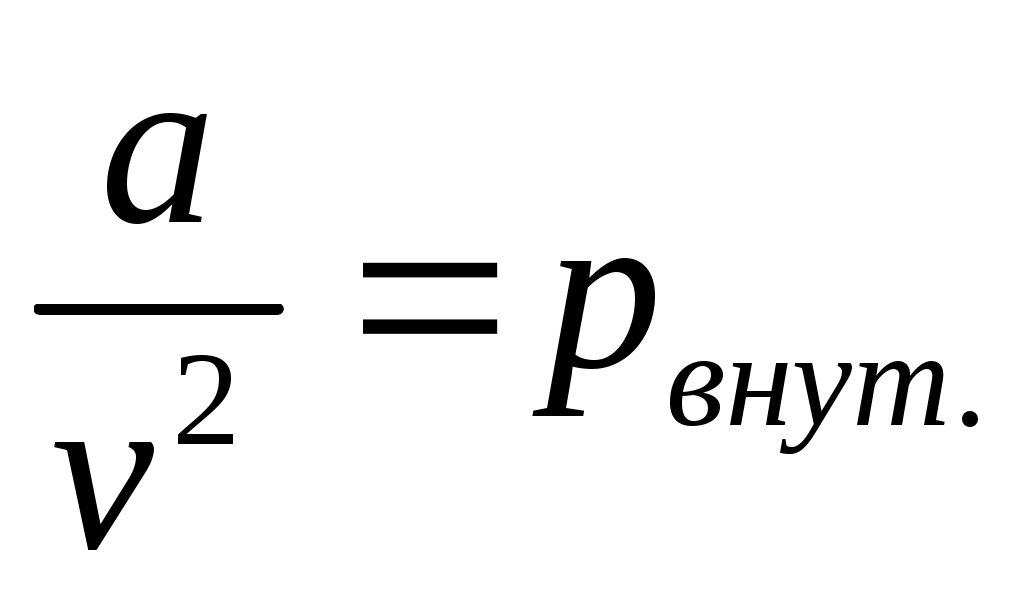 называют внутренним давлением (для жидкостей оно велико), учитывает силы взаимодействия между молекулами;
называют внутренним давлением (для жидкостей оно велико), учитывает силы взаимодействия между молекулами;
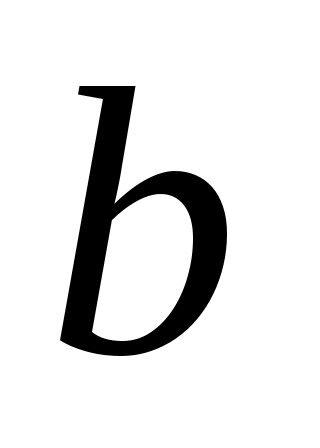 учитывает собственный объем молекул это наименьший объем, до которого можно сжать газ.
учитывает собственный объем молекул это наименьший объем, до которого можно сжать газ.
Для количественных расчетов уравнение (2) часто малопригодно, т.к. при высоких плотностях, а следовательно, при высоких давлениях параметры, рассчитанные по этому уравнению, расходятся с действительными (экспериментальными) значениями.
Уравнение Ван-дер-Ваальса можно представить в приведенных параметрах состояния. Если переменные p, v и T отнести к их значениям в критической точке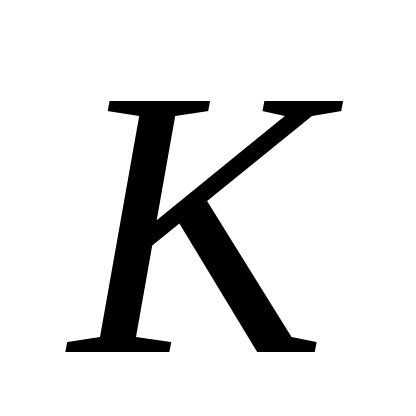
Таким образом, уравнение (12) принимает вид:
Проинтегрировав известное выражение для идеального газа
в интервале температур от t1 до t2, получим:
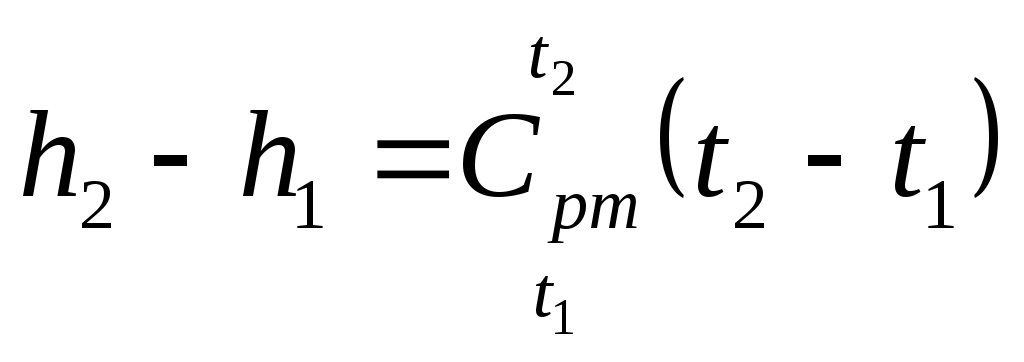 , (15)
, (15)где
Из уравнений (13) и (15) следует:
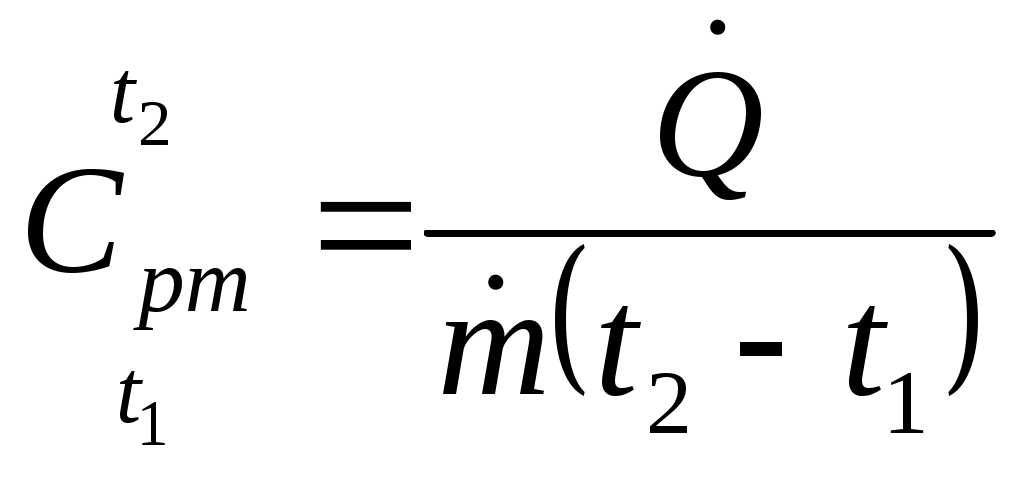 . (16)
. (16)Проведение опытов
-
В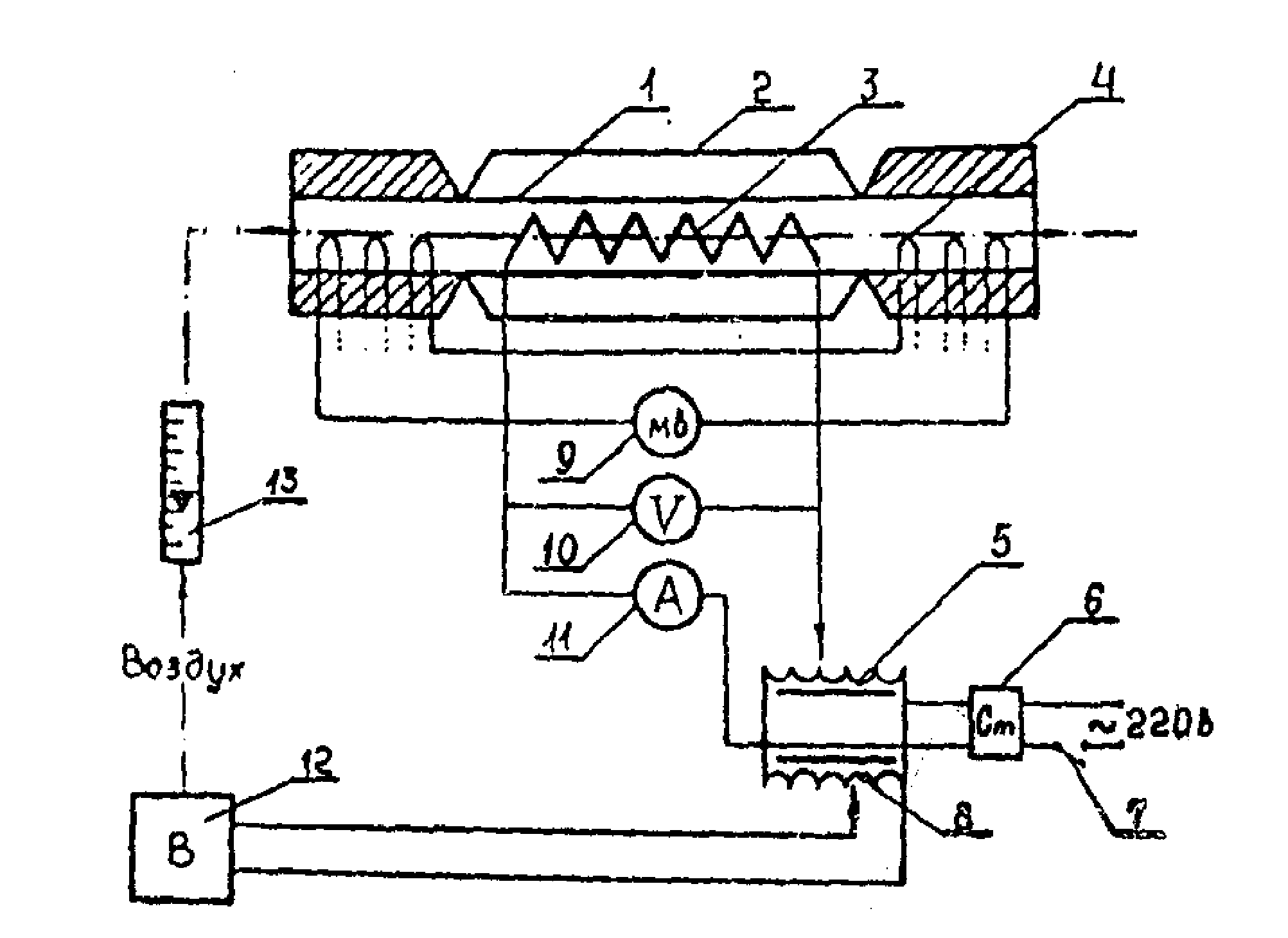
t1
t2
ключить установку (рис. 2).
Рис.2. Схема экспериментальной установки:
1 – проточный калориметр, изготовленный из стекла; 2 – вакууммированная оболочка, предназначенная для уменьшения потерь тепла в окружающую среду; 3 – электронагреватель; 4 – дифференциальная термопара, 5,8 – лабораторные автотрансформаторы; 6 – стабилизатор напряжения; 7 – переключатель; 9 – милливольтметр; 10 – вольтметр; 11 – амперметр; 12 – вентилятор; 13 – ротаметр.
-
Установить заданные значения силы тока и расхода воздуха при помощи трансформаторов 5 и 8. -
П
Нестационарный режим
4 12 20 ,
мин
Рис.3. График стационарности.
е,
мВ
25
15
5
0
Стационарный режим
 осле включения установки, в которой исследуются тепловые процессы, требуется некоторое время, в течение которого происходит стабилизация измеряемых величин. Нестационарный период прогревания элементов установки постепенно сменяется стационарным и измеряемые величины становятся достоверными.
осле включения установки, в которой исследуются тепловые процессы, требуется некоторое время, в течение которого происходит стабилизация измеряемых величин. Нестационарный период прогревания элементов установки постепенно сменяется стационарным и измеряемые величины становятся достоверными.
Н
 а графике стационарности (рис. 3) через каждые 2 мин наносить показания милливольтметра е, мВ до наступления стационарного режима.
а графике стационарности (рис. 3) через каждые 2 мин наносить показания милливольтметра е, мВ до наступления стационарного режима.-
После наступления стационарного режима, о чем свидетельствует неизменность е t2t1 в течение 3-х измерений, занести показания приборов в таблицу опытных данных, таблица 2,
Таблица 2
| Прот. делений | м3/с | I, A | Uэл, В | е, мВ | С | t1, С | t2, С | B, мм рт. ст. | р=В, Па |
| | | | | | | | | | |
где Прот. – показания ротаметра;
Обработка опытных данных
-
Рассчитать значения теплоемкостей и некоторые характеристики процесса. Результаты занести в таблицу обработки опытных данных (таблица 3).
Таблица 3
| Расчетная величина | Формула | Значение |
| Тепловой поток, выделяемый в электронагревателе | | |
| Массовый расход воздуха | | |
| Средняя массовая изобарная теплоемкость воздуха в интервале температур t1 и t2 | 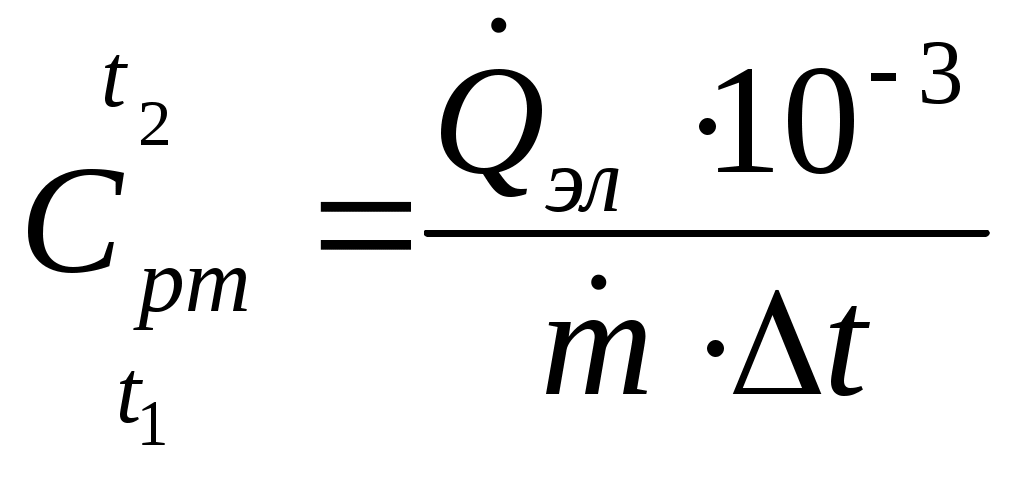 , кДж/(кгград) , кДж/(кгград) | |
| Средняя массовая изохорная теплоемкость воздуха в интервале температур t1 и t2 | 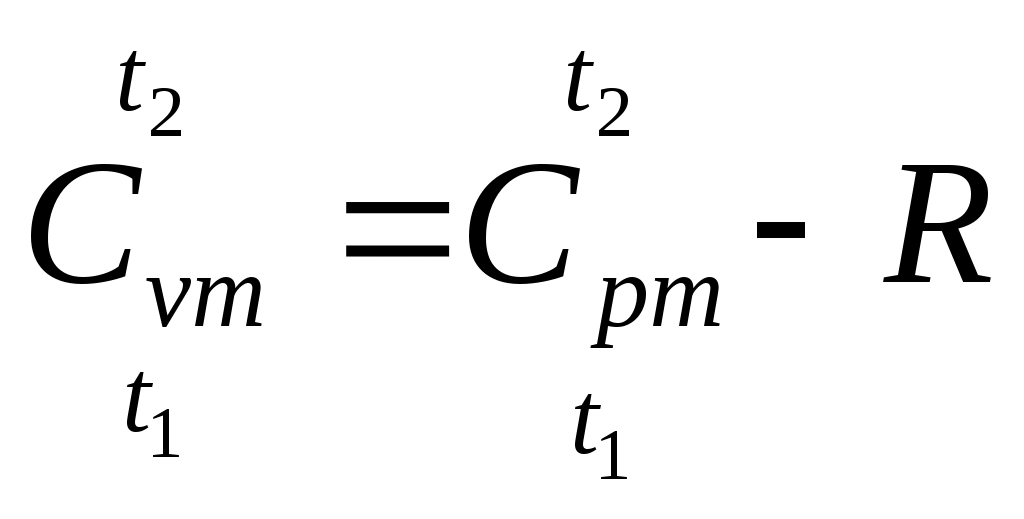 , кДж/(кгград) , кДж/(кгград)где | |
| Изменение внутренней энергии | 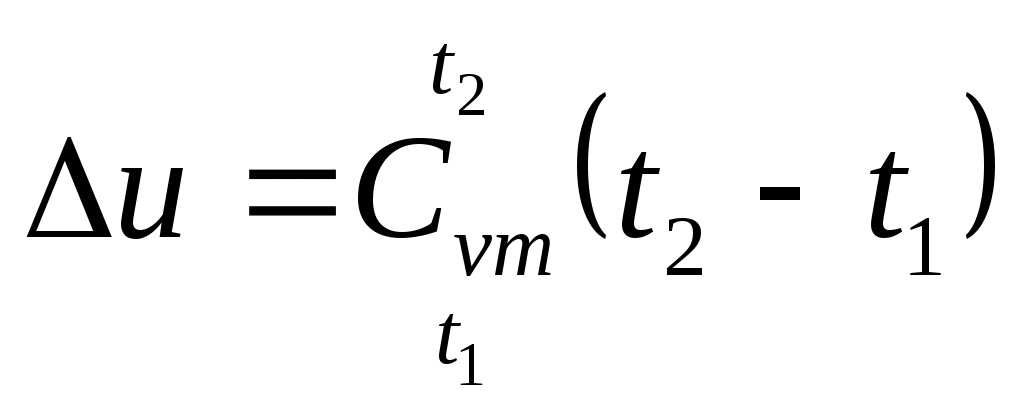 , кДж/кг , кДж/кг | |
| Изменение энтальпии | 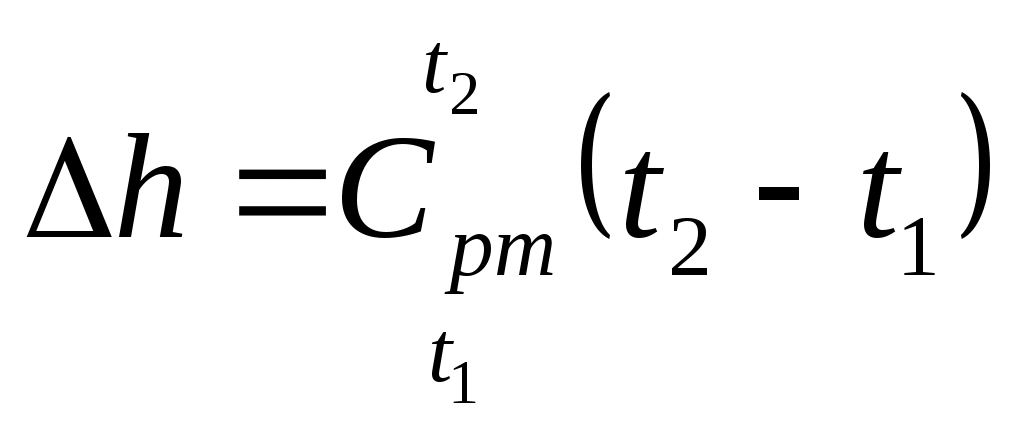 , кДж/кг , кДж/кг | |
| Изменение энтропии в процессе при | 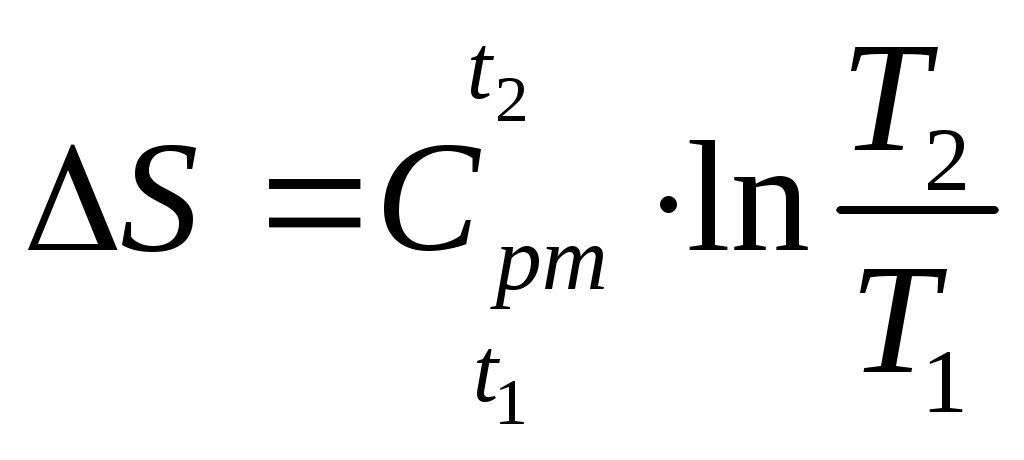 , кДж/(кгград) , кДж/(кгград) | |
| Изменение энтропии в процессе при | 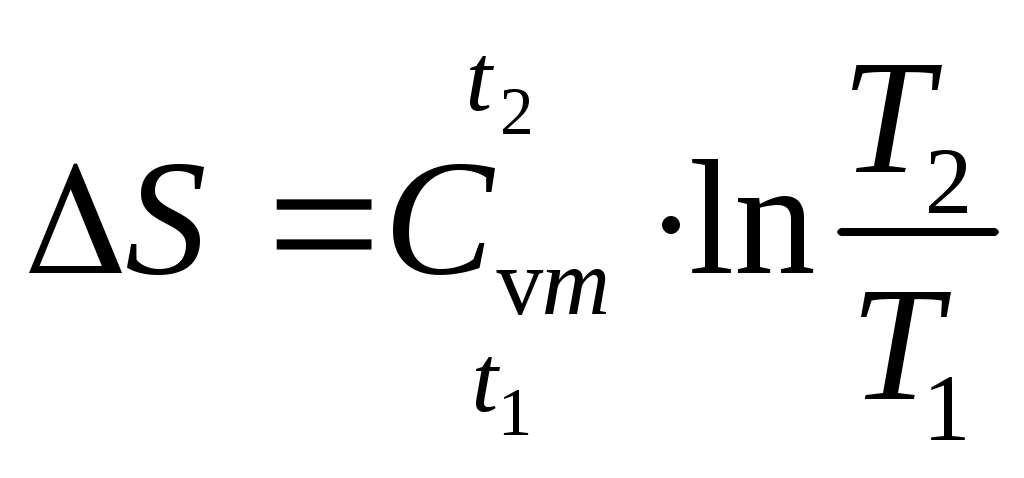 , кДж/(кгград) , кДж/(кгград) | |
| Показатель адиабаты | | |
-
Определить теплоемкости Сvи Cp воздуха, используя молекулярно-кинетическую теорию газов (таблица 1) и соотношения (11).
Вычислить расхождения с экспериментальными данными
-
Рассчитать систематическую погрешность измерений при экспериментальном определении Срт:
Подробно материал к этому пункту изложен в разделе «Оценка погрешности эксперимента».
Контрольные вопросы
-
Удельные теплоемкости газов. Определение, обозначения и размерности. Использование для расчетов Qx. -
Зависимость теплоемкости от характера процесса подвода теплоты. Уравнение Майера. -
Зависимость теплоемкости от температуры. Понятие о средней теплоемкости. -
Сущность метода проточного калориметрирования. Схема экспериментальной установки. -
Первый закон термодинамики для газового потока. Расчетное выражение для определения теплоемкости. -
Методика расчета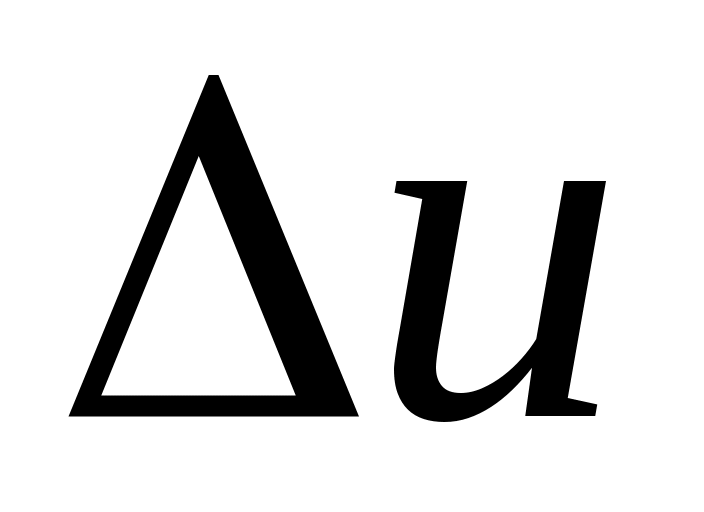 ,
,  и
и .
. -
Элементы молекулярно-кинетической теории теплоемкости. -
Понятие об истинной теплоемкости и ее связи со средней теплоемкостью. -
Техника проведения теплотехнического эксперимента. Понятие о стационарном режиме.
Лабораторная работа № 23
Исследование pv-диаграммы углекислого газа.
Опыт Эндрюса
Цель работы: ознакомиться с общими свойствами идеальных и реальных газов; освоить методику экспериментального определения зависимости p-v-t реальных газов.
Задание.
-
Провести опыты по изотермическому сжатию углекислого газа (СО2) при температурах, указанных преподавателем: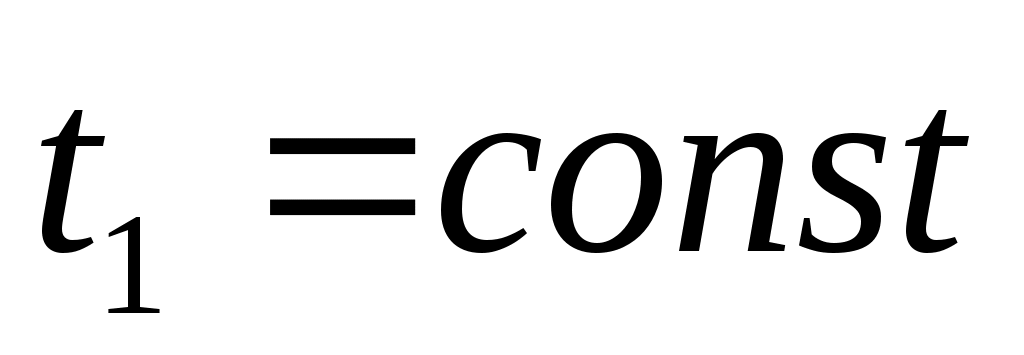 ,
, 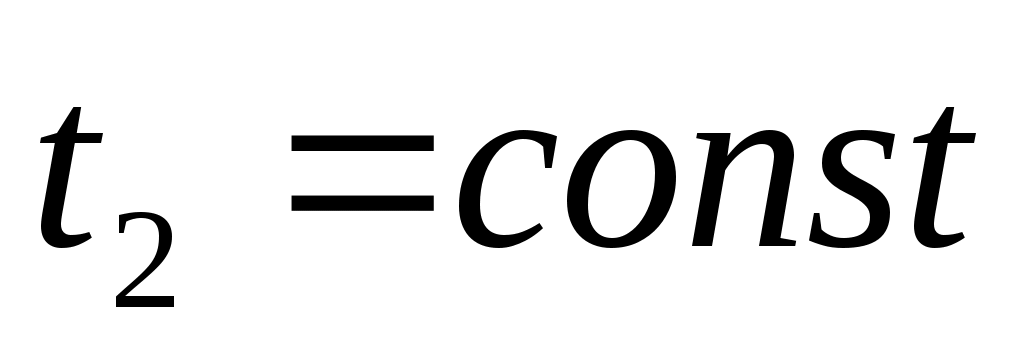 ,
, 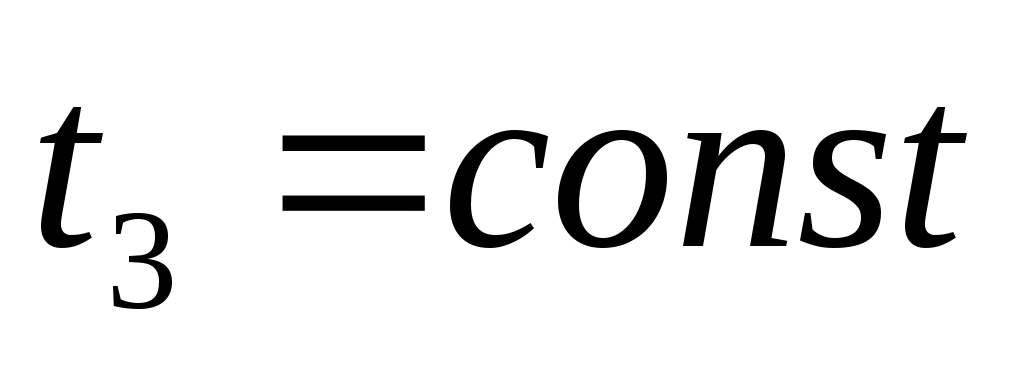 .
. -
На основании опытных данных построить pv-диаграмму для исследованного газа. -
Рассчитать коэффициент неидеальности .
. -
Составить отчет о выполненной работе, который должен содержать: задание, основы теории (кратко), схему экспериментальной установки, таблицу опытных данных, результаты обработки и pv-диаграмму, выполненную на миллиметровой бумаге.
Основы теории
Идеальным газом называется воображаемый газ, молекулы которого представляют собой материальные точки, не имеющие собственного объема и не взаимодействующие между собой. Зависимость между основными термодинамическими параметрами такого газа определяется уравнением состояния идеального газа – уравнением Клапейрона-Менделеева:
где
Реальные газы состоят из молекул, имеющих конечный собственный объем, между которыми действуют силы межмолекулярного взаимодействия (силы притяжения и отталкивания). Эти газы описываются уравнением (1) только при малых плотностях, когда среднее расстояние между центрами молекул сравнительно велико, и эти силы не проявляются. В более плотных реальных газах со значительно меньшим расстоянием между молекулами необходимо учитывать и эти силы, и собственный объем молекул. Поведение реальных газов качественно отражает уравнение Ван-дер-Ваальса:
где
Для количественных расчетов уравнение (2) часто малопригодно, т.к. при высоких плотностях, а следовательно, при высоких давлениях параметры, рассчитанные по этому уравнению, расходятся с действительными (экспериментальными) значениями.
Уравнение Ван-дер-Ваальса можно представить в приведенных параметрах состояния. Если переменные p, v и T отнести к их значениям в критической точке