ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 92
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(далее в опыте Эндрюса эта точка будет рассмотрена подробнее), то можно получить приведенные значения объема 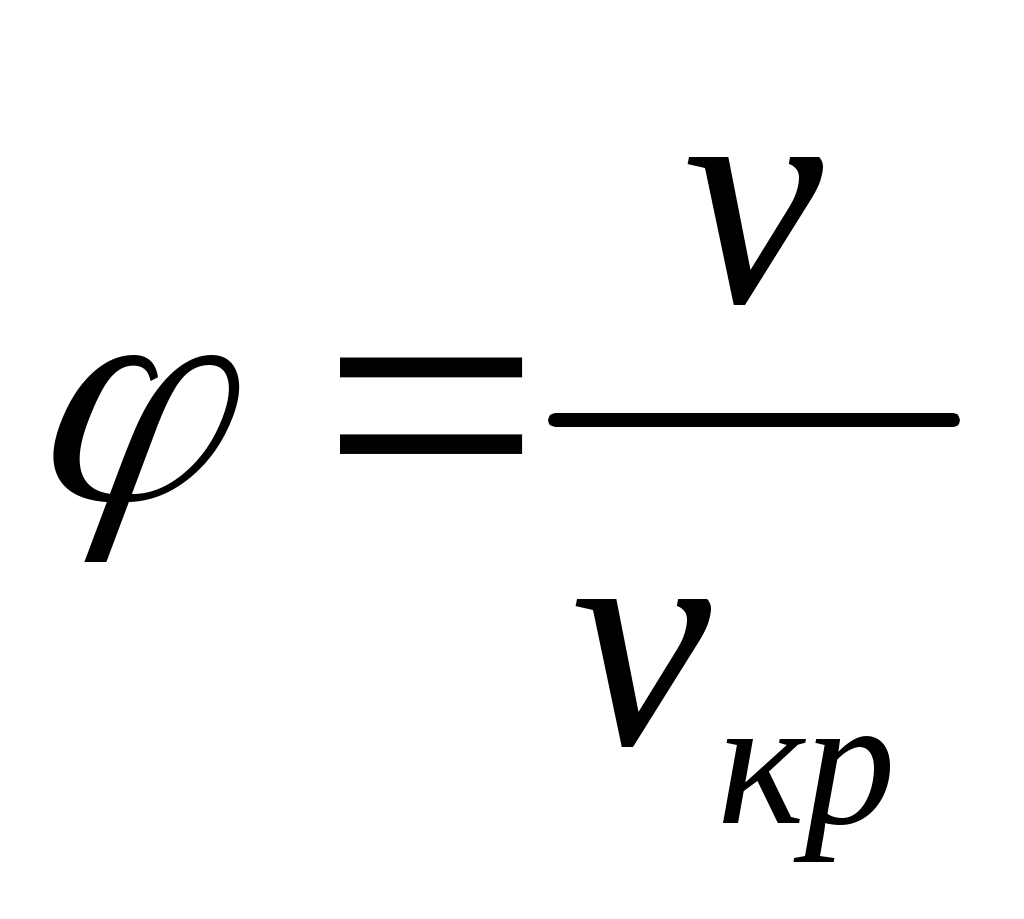 , давления
, давления 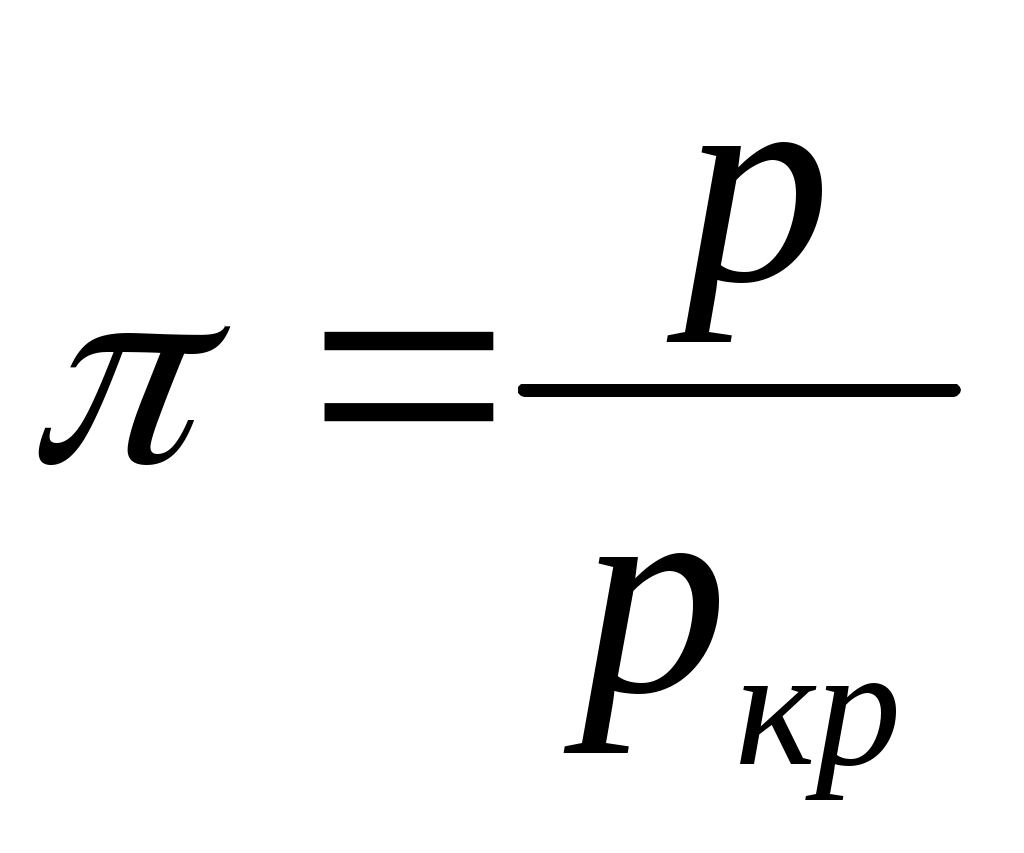 и температуры
и температуры 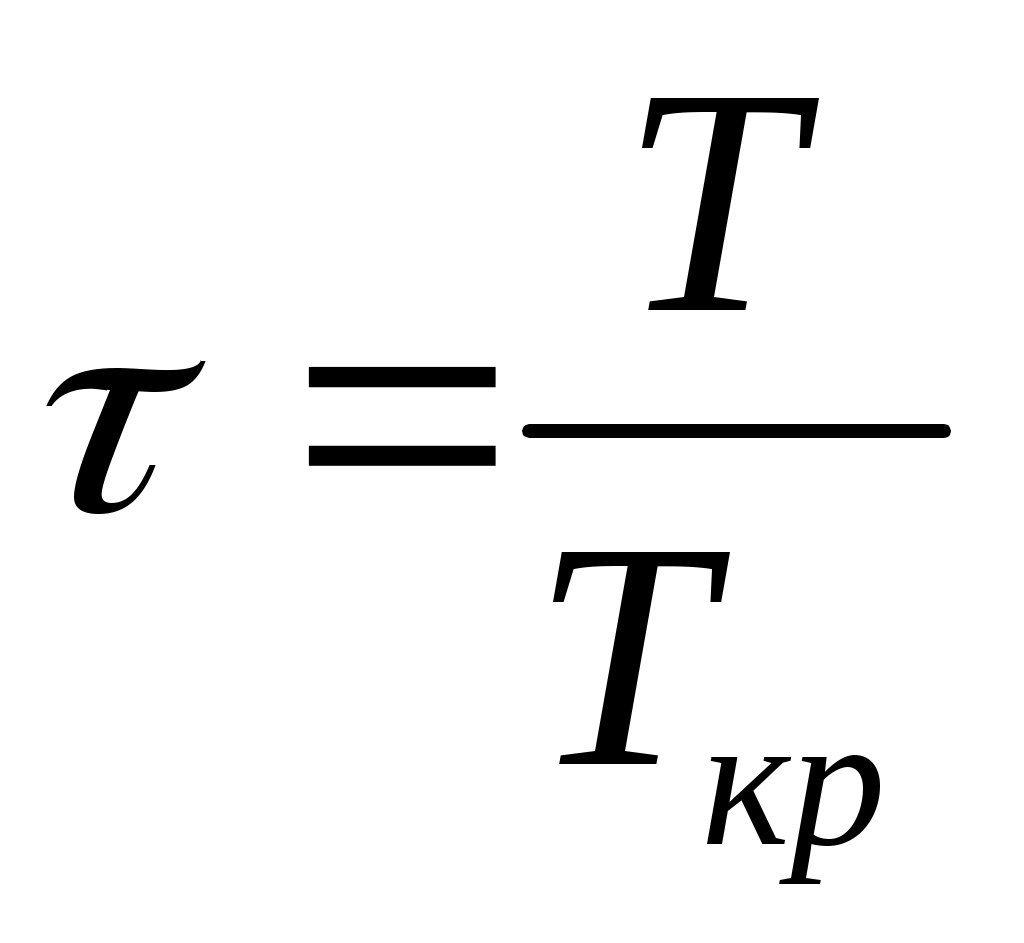 и записать так называемое приведенное уравнение состояния:
и записать так называемое приведенное уравнение состояния:
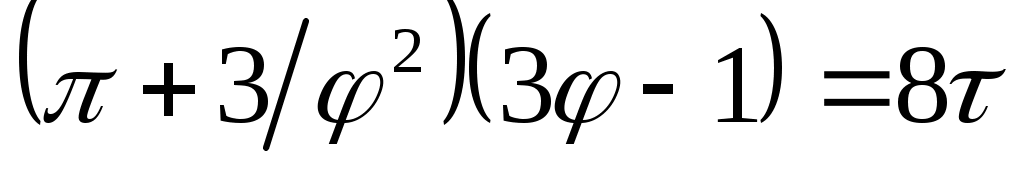 . (3)
. (3)
Состояния веществ, находящихся при одинаковых ,
,  и
и  , называются соответственными состояниями.
, называются соответственными состояниями.
Уравнения типа (2) и (3) получаются в случае, если ограничиться рассмотрением только парных взаимодействий между молекулами, т.е. в группах по две молекулы. Поэтому эти уравнения применимы в области не очень высоких давлений.
С повышением давления необходимо учитывать образование устойчивых молекулярных образований из трех, четырех и более молекул, распад которых возможен только при подводе энергии извне, т.е. при нагревании. Такой газ можно рассматривать как «смесь» нескольких газов, частицами которых являются одиночные, двойные, тройные и т.д. группы молекул.
Уравнение состояния реальных газов формально можно записать в виде:
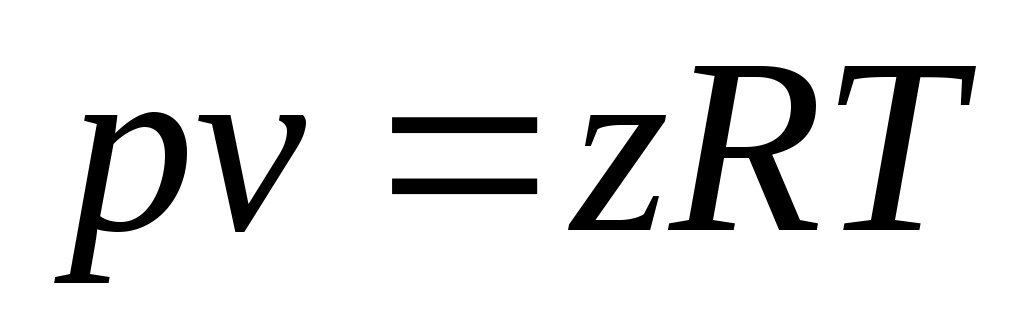 , (4)
, (4)
где z коэффициент сжимаемости (для идеальных газов z = 1) можно представить в виде вириального уравнения, учитывающего и взаимодействия более высокого порядка:
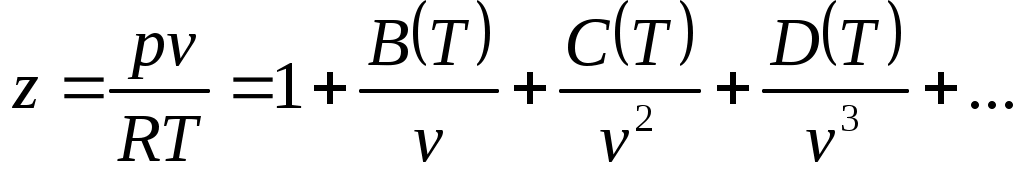 . (5)
. (5)
Правую часть этого уравнения можно рассматривать как разложение в ряд коэффициента z по степеням плотности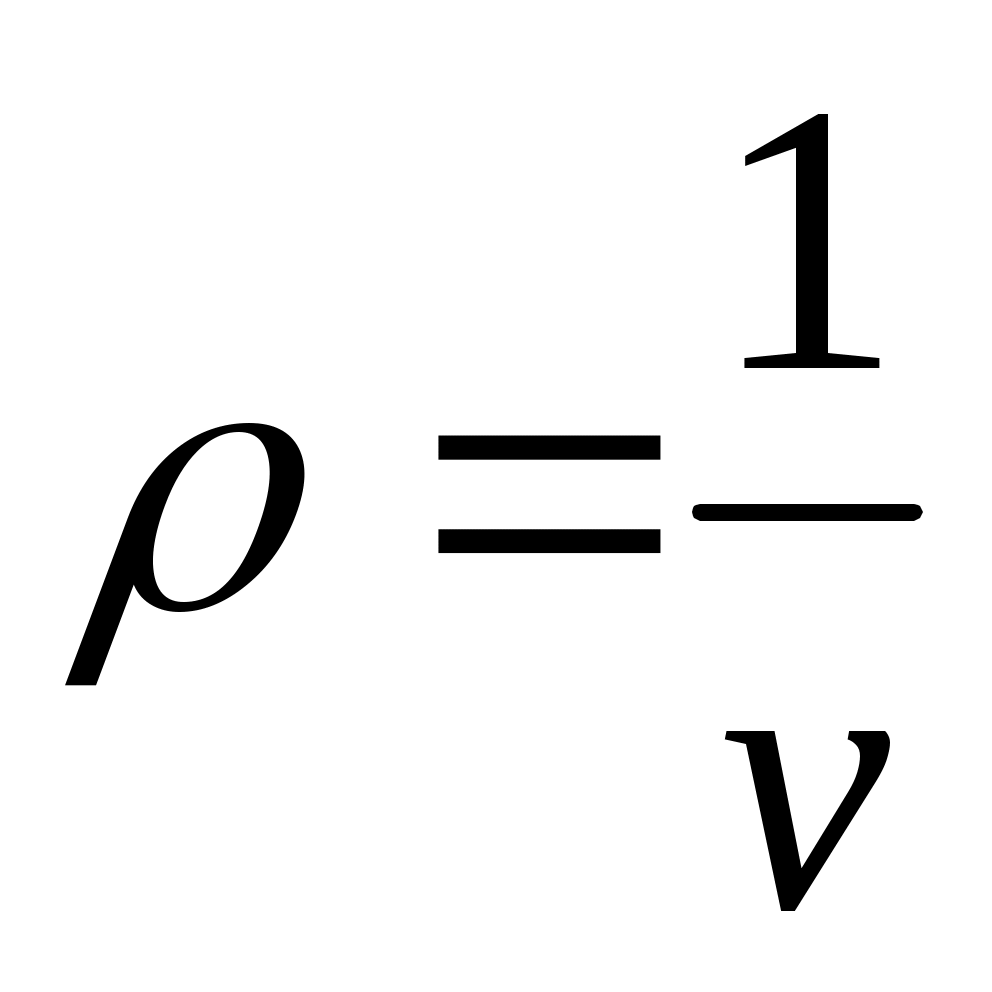 . Зависящие от температуры функции
. Зависящие от температуры функции 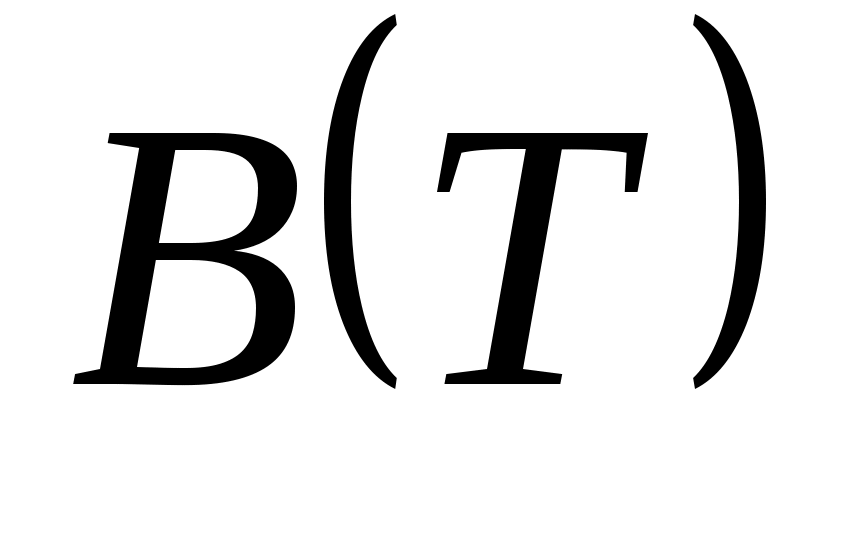 ,
, 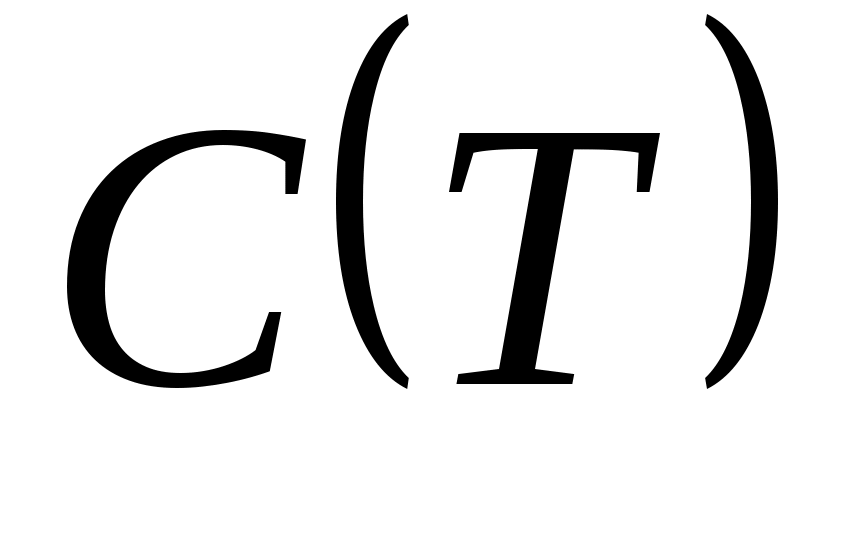 ,
, 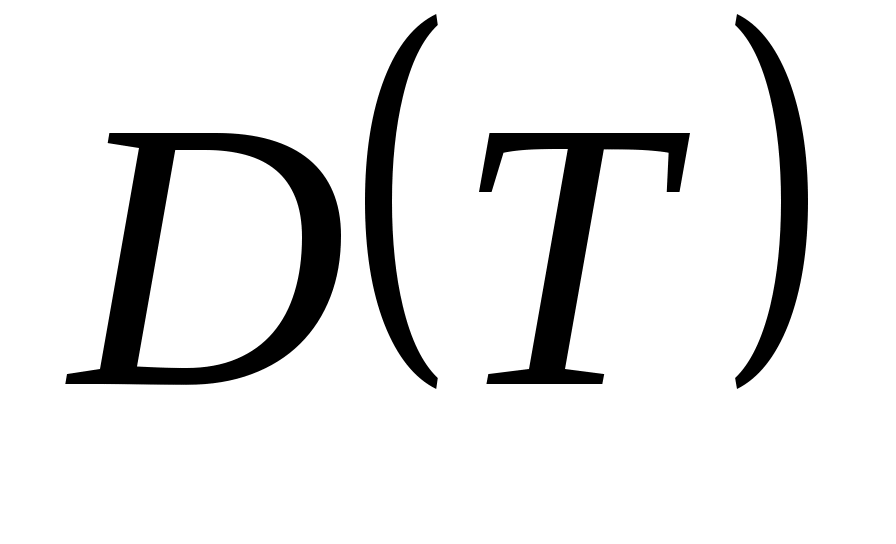 … выступают здесь как вириальные (от латинского vires силы) коэффициенты, учитывающие соответственно парные, тройные, четверные и т.д. взаимодействия. Область справедливости вириального разложения ограничивается сходимостью рядов. Ряды расходятся при плотностях, соответствующих жидкому состоянию. Уравнение (5) оказывается справедливым для газов умеренной плотности.
… выступают здесь как вириальные (от латинского vires силы) коэффициенты, учитывающие соответственно парные, тройные, четверные и т.д. взаимодействия. Область справедливости вириального разложения ограничивается сходимостью рядов. Ряды расходятся при плотностях, соответствующих жидкому состоянию. Уравнение (5) оказывается справедливым для газов умеренной плотности.
Второй вириальный коэффициент может быть определен по значениям потенциальной энергии взаимодействия силам притяжения и отталкивания двух молекул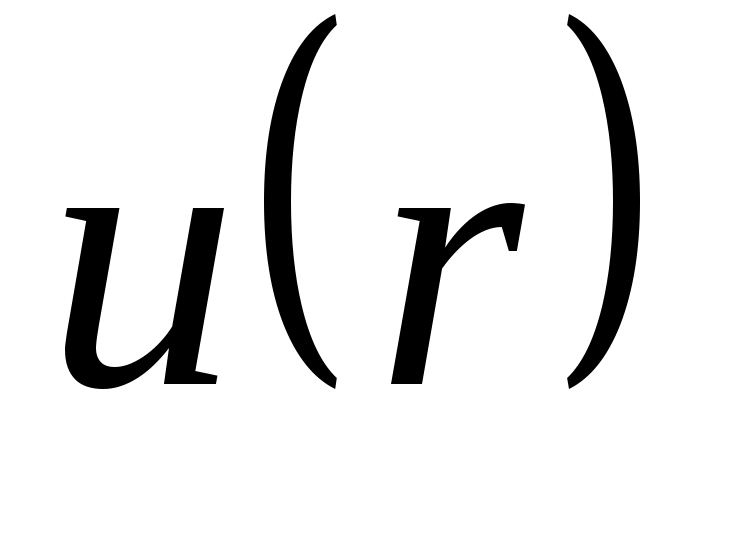 в зависимости от расстояния между ними:
в зависимости от расстояния между ними:
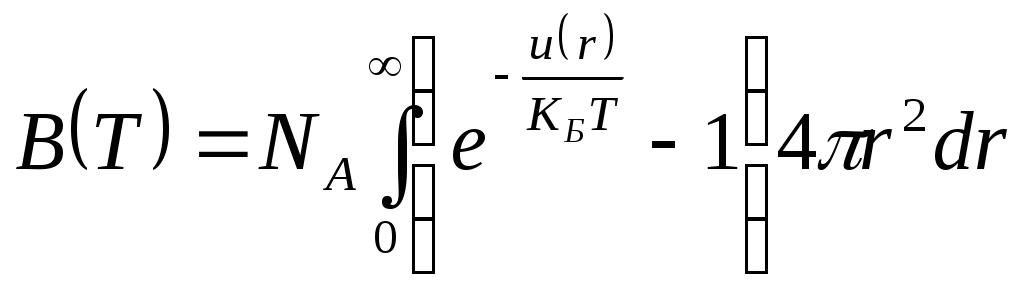 , (6)
, (6)
где NA число Авогадро, NA = 6,0221026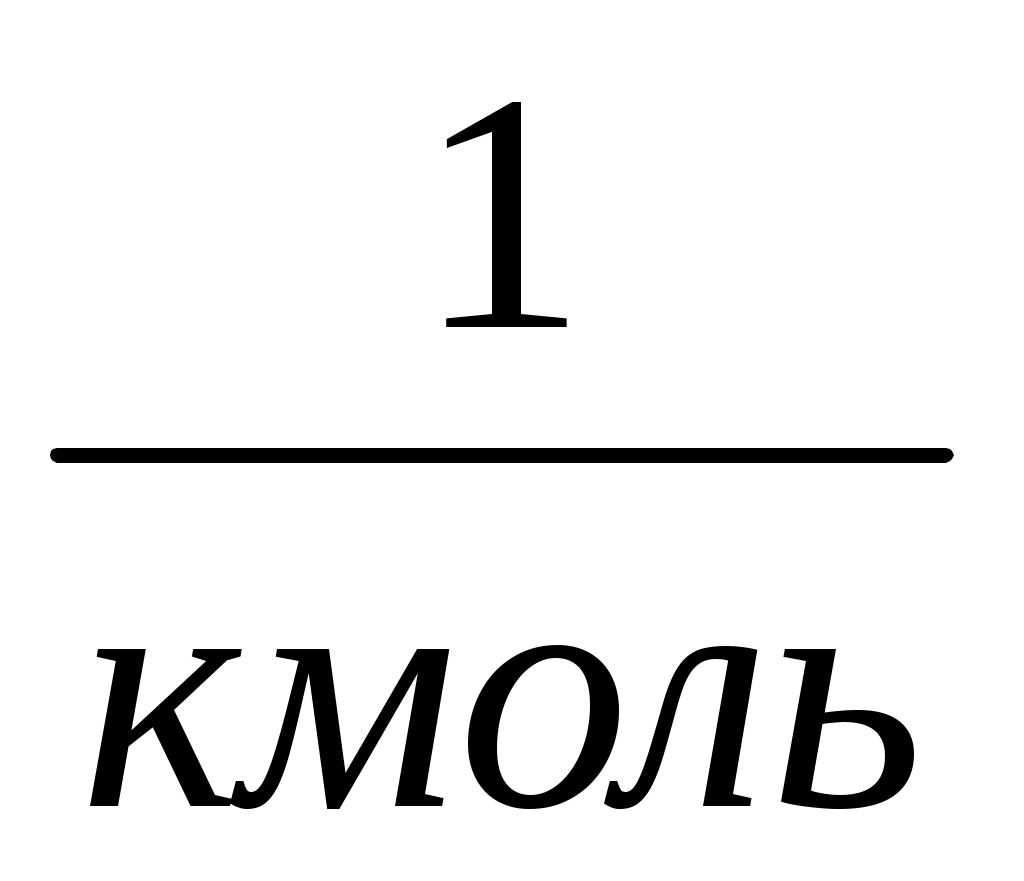 ;
;
КБ постоянная Больцмана, КБ = 1,3810-23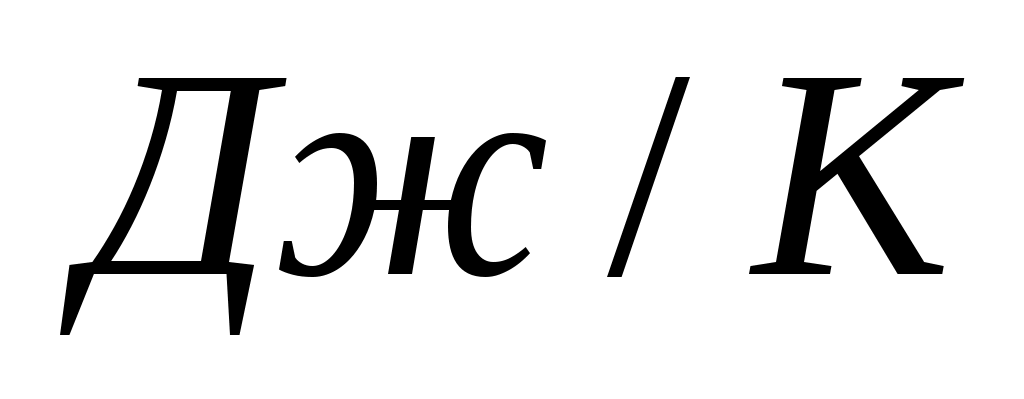 ;
;
кстати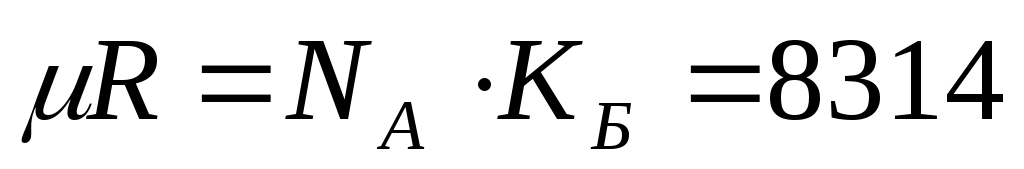
 универсальная газовая постоянная.
универсальная газовая постоянная.
Определение последующих вириальных коэффициентов для газов достаточно большой плотности облегчается при наличии экспериментально полученных данных по теплофизическим свойствам этих газов (теплоемкость, вязкость, теплопроводность и т.п.).
К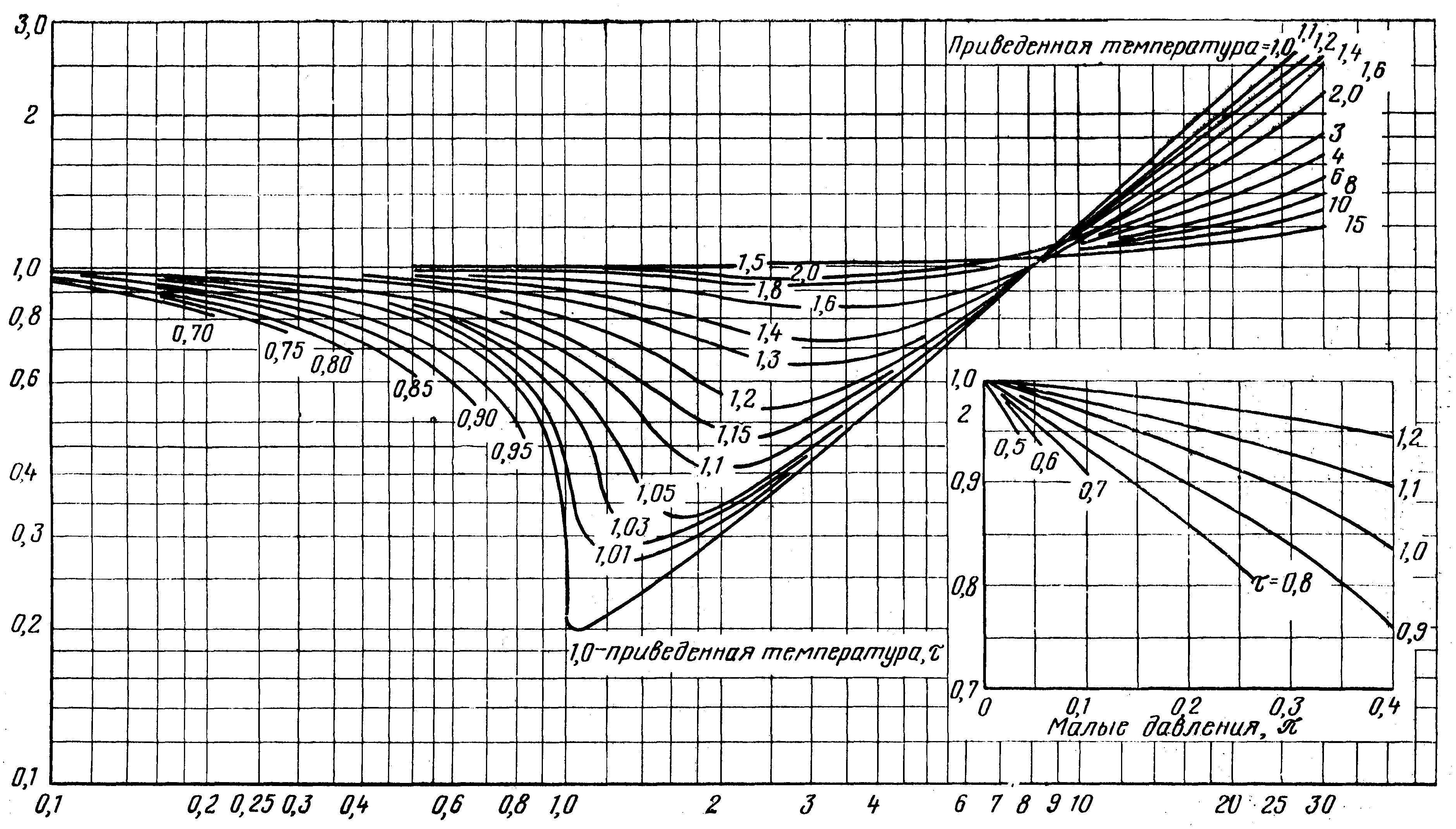
оэффициент неидеальности z может быть найден также по зависимости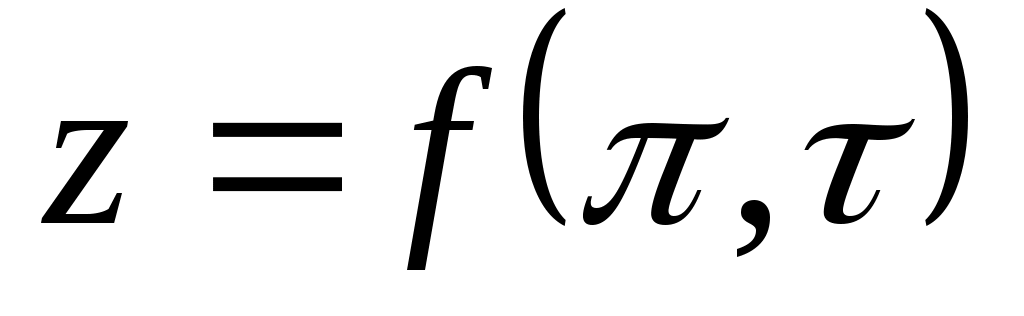 из
из 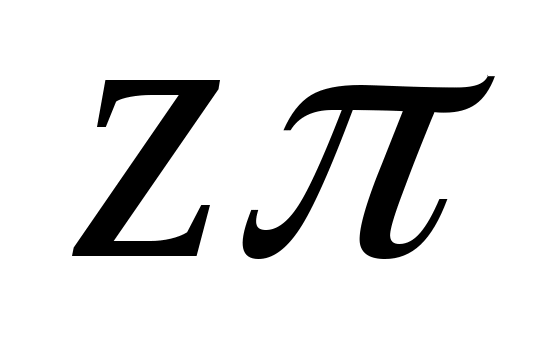 - диаграммы (рис.1).
- диаграммы (рис.1).
Р
z
ис.1. z–диаграмма реального газа.
Рассчитанное значение откладывается на соответствующей оси этой диаграммы и из этой точки проводится прямая, перпендикулярная оси
откладывается на соответствующей оси этой диаграммы и из этой точки проводится прямая, перпендикулярная оси  до пересечения с кривой, соответствующей рассчитанному значению . Точка пересечения позволяет определить искомую величину коэффициента неидеальности на оси z .
до пересечения с кривой, соответствующей рассчитанному значению . Точка пересечения позволяет определить искомую величину коэффициента неидеальности на оси z .
Точность расчетов в этом случае окажется такой же, как и по уравнению Ван-дер-Ваальса (2) или приведенному уравнению (3)
Опыт Эндрюса
Свойства реальных газов не только в количественном, но и в качественном отношении отличаются от свойств реальных газов. Теория идеальных газов не может объяснить фазовые превращения газа и жидкости, она не может установить границы области фазовых переходов, параметры критического состояния.
В 1869 г. английский физик Эндрюс впервые на основании проведенных им экспериментов по изотермическому сжатию СО2 построил pv-диаграмму для реального газа и показал на ней характерные граничные линии и области состояний.
Р
2”
2’
2
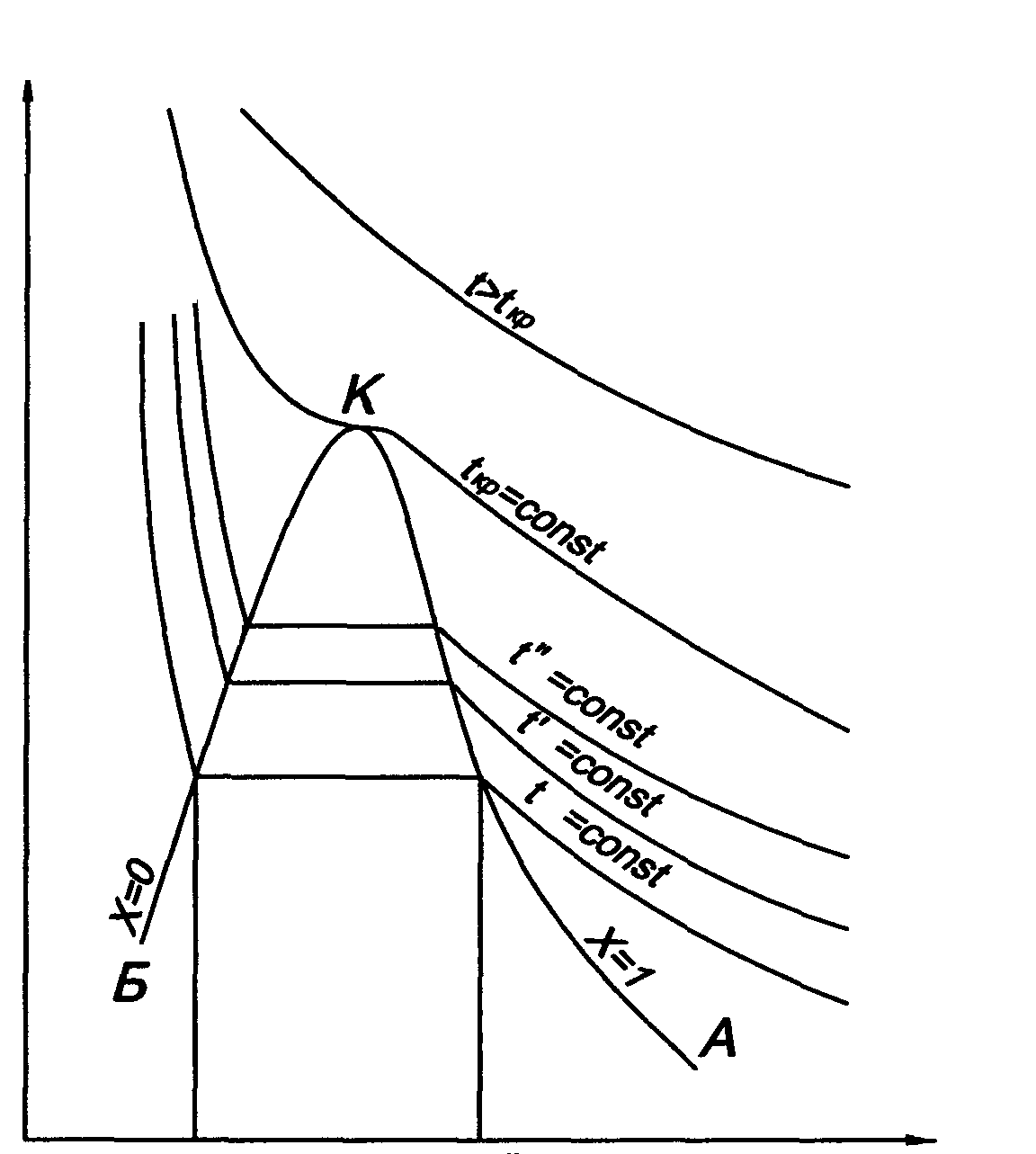
Рис.2. pv-диаграмма реальных газов
р
v
4”
4’
4
1 ”
1’
1
р
анее было известно, что одни газы путем сжатия при комнатной температуре удается перевести в жидкое состояние, другие нет. Не было объяснения этому явлению.
П
v
4”
4’
4
1”
1’
1
3”
3’
3
2”
2’
2
роследить за поведением газа в процессе изотермического (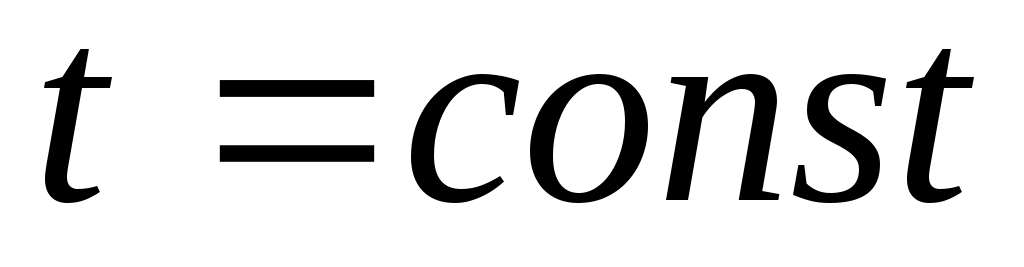 ) сжатия можно по pv-диаграмме, рис. 2. Участок 1-2 кривой сжатия соответствует изменению параметров p и v газообразного состояния вещества. В точке 2 давление газа достигает величины рн – давления насыщения при данной температуре t и газ начинает конденсироваться при
) сжатия можно по pv-диаграмме, рис. 2. Участок 1-2 кривой сжатия соответствует изменению параметров p и v газообразного состояния вещества. В точке 2 давление газа достигает величины рн – давления насыщения при данной температуре t и газ начинает конденсироваться при 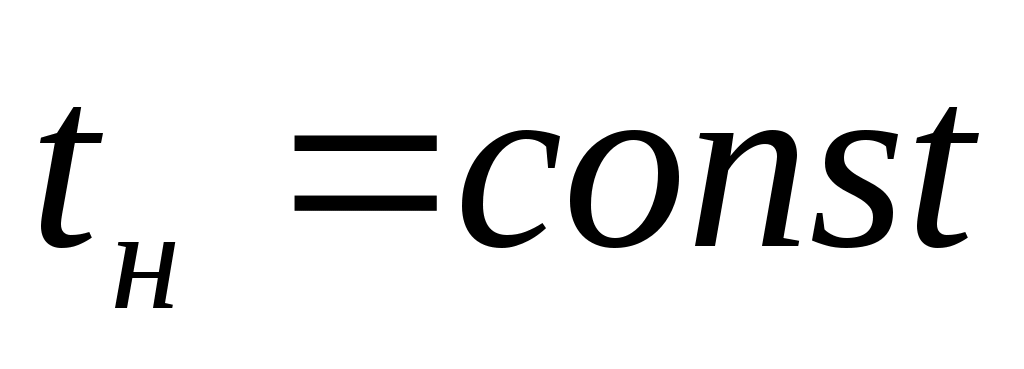 и
и 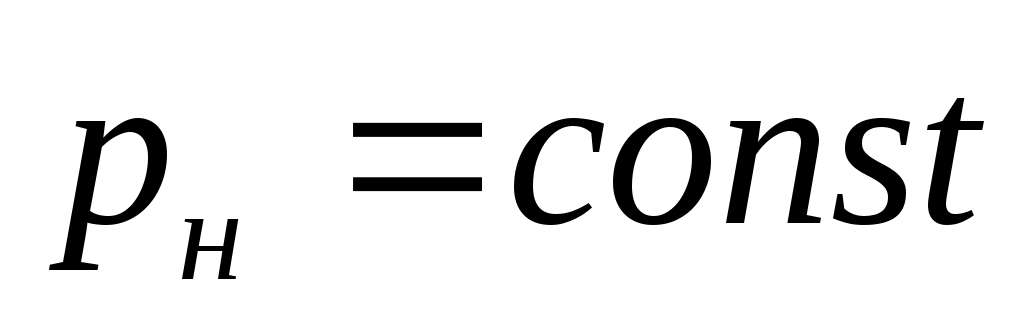 , процесс 2-3.
, процесс 2-3.
В точке 3 процесс конденсации завершается.
Кривая 3-4 соответствует процессу сжатия жидкой фазы при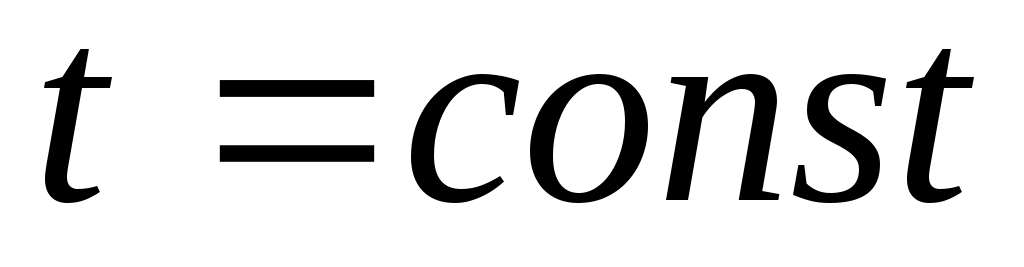 . Поскольку жидкость плохо сжимается, объем здесь меняется мало, а давление резко возрастает.
. Поскольку жидкость плохо сжимается, объем здесь меняется мало, а давление резко возрастает.
Исследуя зависимость vот р на разных изотермах t, t’, t” и т.д., Эндрюс установил, что чем выше температура, тем меньше разница между удельными объемами сухого насыщенного пара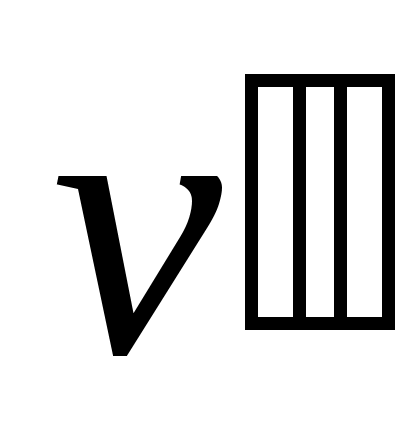 и насыщенной жидкости
и насыщенной жидкости 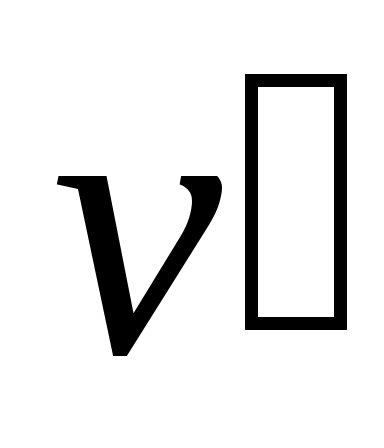 . С повышением температуры
. С повышением температуры 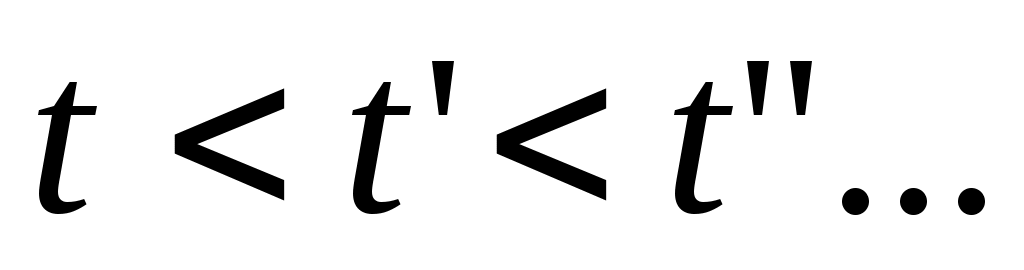 точки 2,
точки 2, 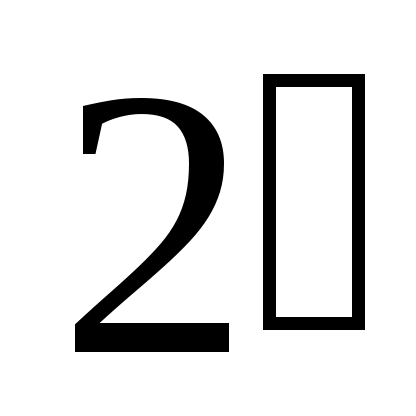 ,
,  …, образующие верхнюю пограничную кривую АК (линия сухого насыщенного пара
…, образующие верхнюю пограничную кривую АК (линия сухого насыщенного пара
, x = 1), сближаются соответственно с точками 3, ,
,  …, образующими нижнюю пограничную кривую БК (линия кипящей жидкости, х = 0). Здесь х – степень сухости,
…, образующими нижнюю пограничную кривую БК (линия кипящей жидкости, х = 0). Здесь х – степень сухости,
х =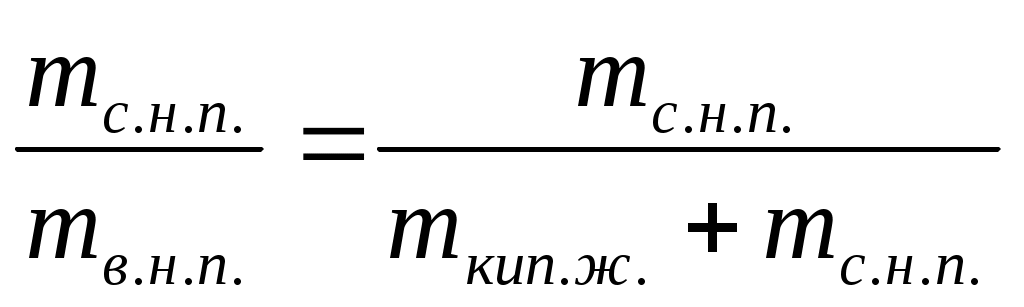 ,
,
где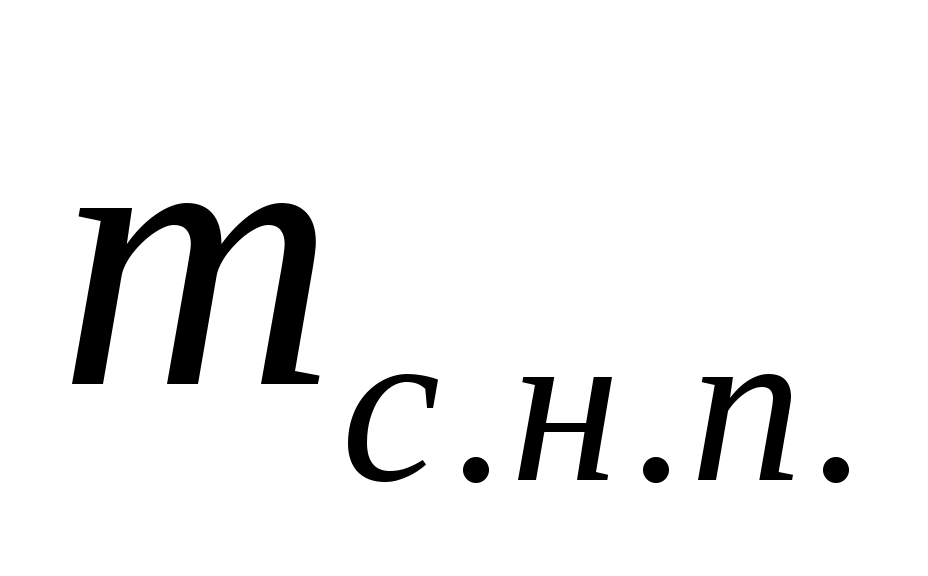 масса сухого насыщенного пара,
масса сухого насыщенного пара,
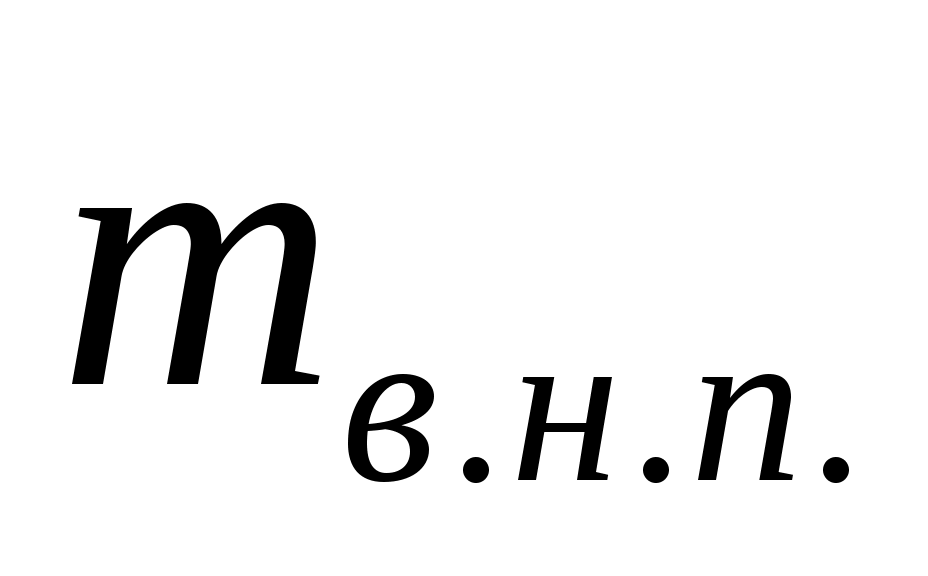 масса влажного насыщенного пара – смеси кипящей жидкости и сухого насыщенного пара.
масса влажного насыщенного пара – смеси кипящей жидкости и сухого насыщенного пара.
Разность удельных объемов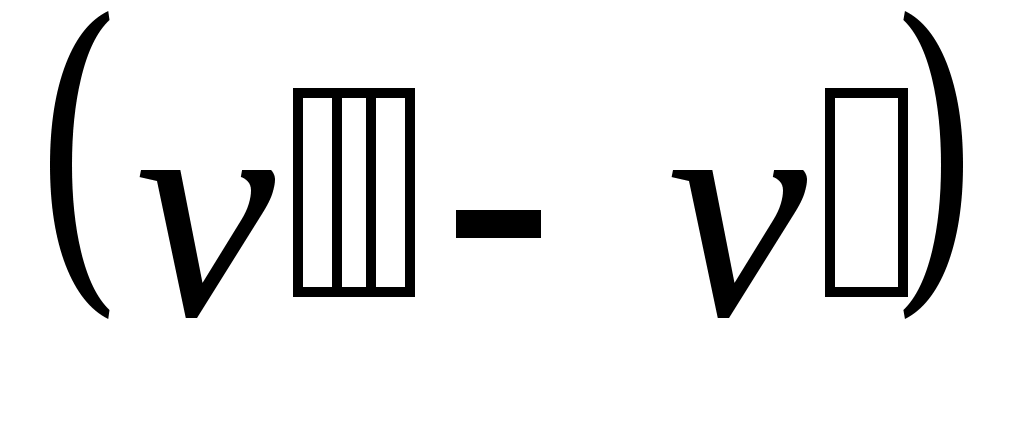 уменьшается до тех пор, пока при некоторой температуре tкр не станет равной нулю, т.е.
уменьшается до тех пор, пока при некоторой температуре tкр не станет равной нулю, т.е. 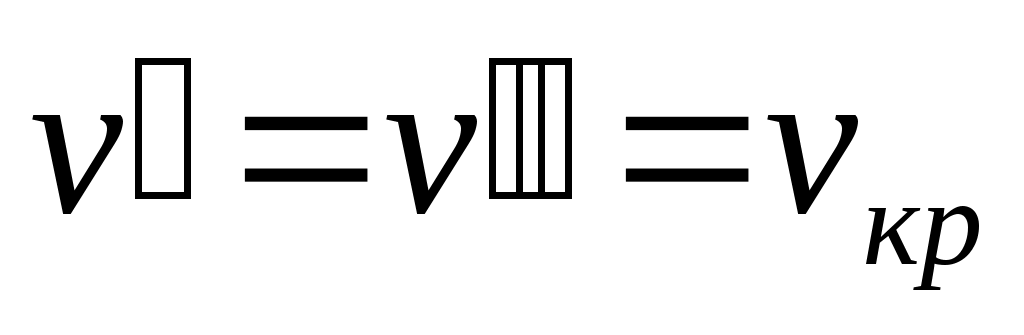 . Состояние в точке К с параметрами ркр, vкр и tкр назвали критическим. В этой точке исчезают различия между жидкой и газовой фазами.
. Состояние в точке К с параметрами ркр, vкр и tкр назвали критическим. В этой точке исчезают различия между жидкой и газовой фазами.
Таким образом, для реального газа в pv-диаграмме можно выделить три характерные области:
Нетрудно видеть, что при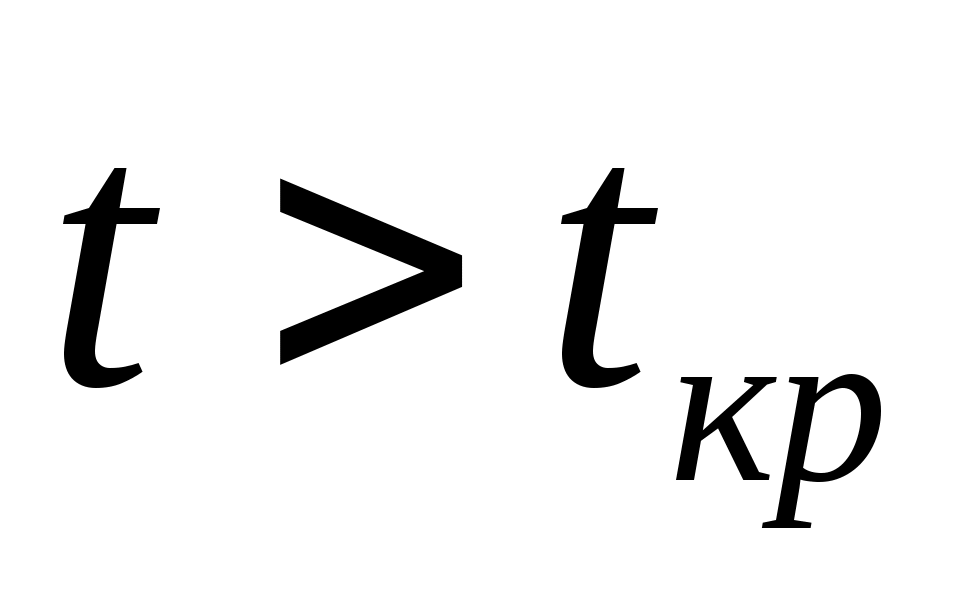 путем простого изотермического сжатия попасть в область фазовых переходов нельзя. Этим объясняется то, что газы, у которых
путем простого изотермического сжатия попасть в область фазовых переходов нельзя. Этим объясняется то, что газы, у которых 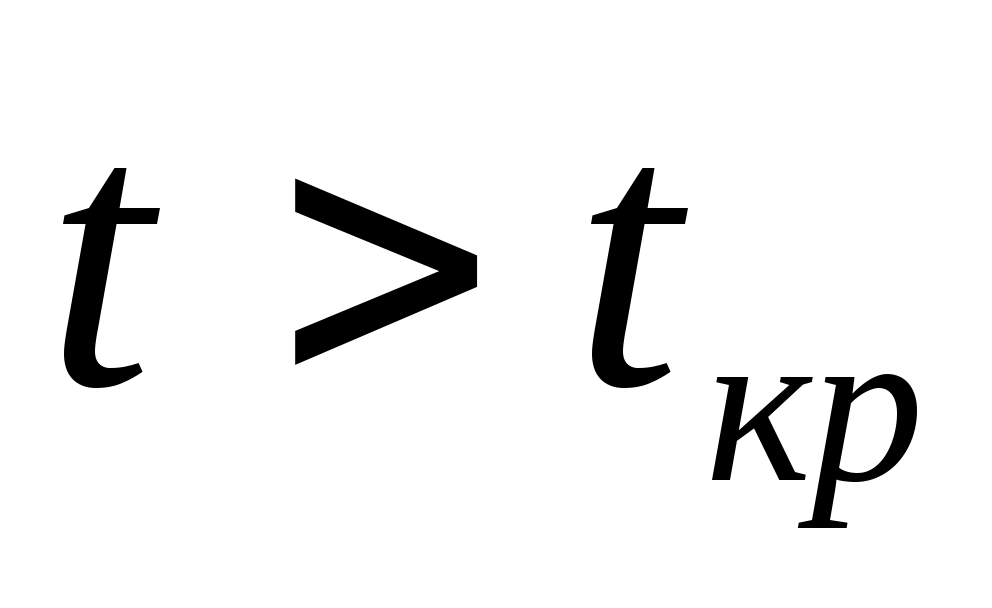 , без понижения температуры не переходят в жидкое состояние.
, без понижения температуры не переходят в жидкое состояние.
В таблице 1 приведены критические параметры некоторых реальных газов.
Таблица 1
Вещество в критическом состоянии имеет ряд особенностей. Критическая изотерма tкр. в критической точке К имеет горизонтальную касательную и перегиб, т.е.
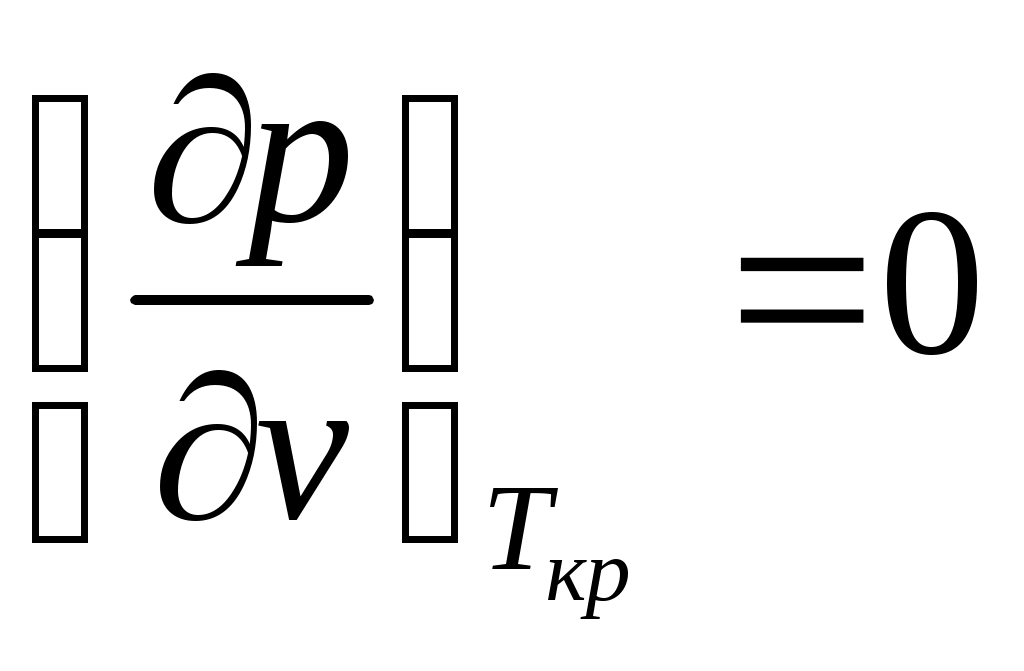 и
и 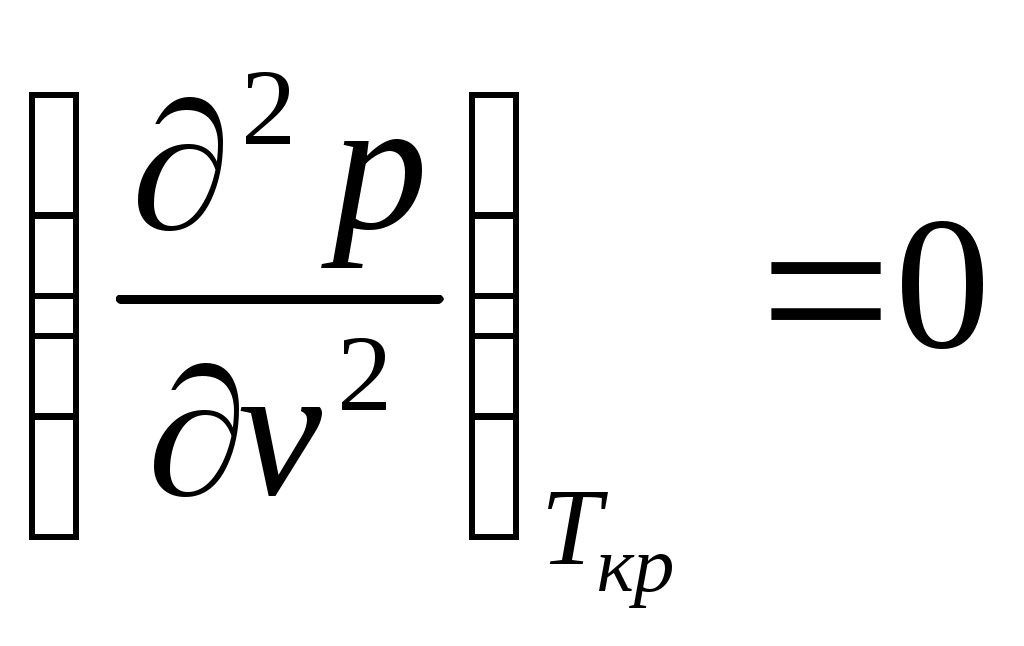 . (7)
. (7)
Вблизи этой точки наблюдается скачек теплоемкости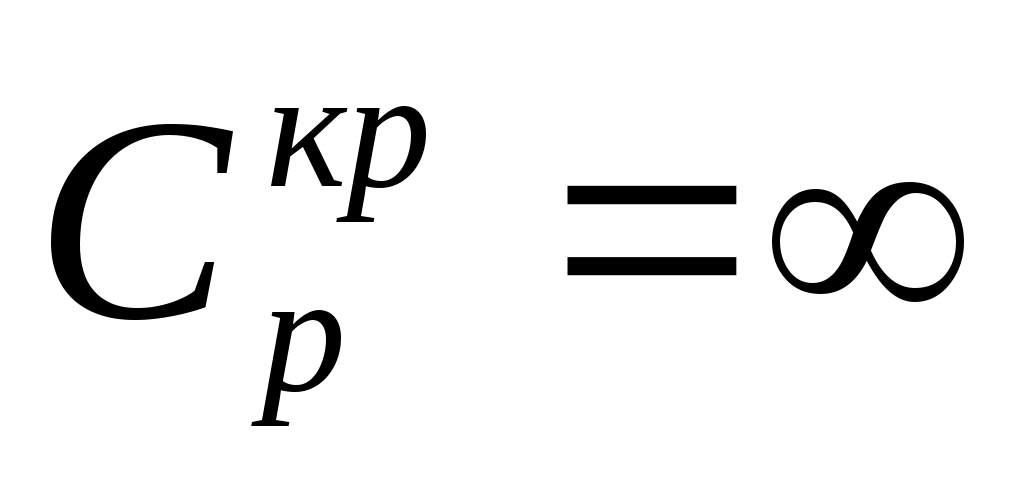 . В точке К теплота парообразования
. В точке К теплота парообразования 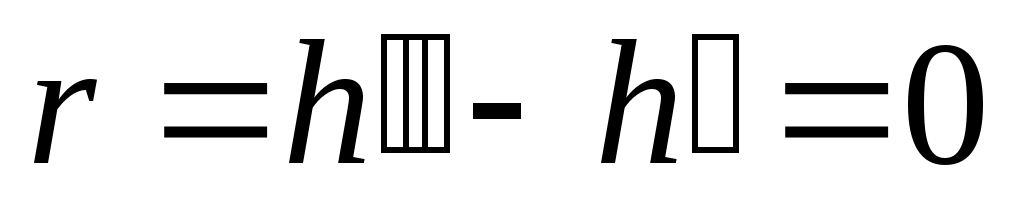 , становятся равными нулю силы поверхностного натяжения
, становятся равными нулю силы поверхностного натяжения 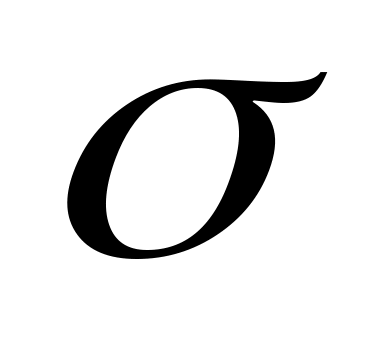 , которые являются наиболее ярким проявлением межмолекулярного взаимодействия. Поэтому в этой точке отсутствует межфазная поверхность, здесь наблюдается высокая растворяющая способность вещества.
, которые являются наиболее ярким проявлением межмолекулярного взаимодействия. Поэтому в этой точке отсутствует межфазная поверхность, здесь наблюдается высокая растворяющая способность вещества.
Особые свойства веществ в критической и околокритической областях состояния в настоящее время уже находят применение в пищевой, фармацевтической, парфюмерной, химической, нефте- и углеперерабатывающей отраслях промышленности, в решении экологических проблем. В частности, «предложено использование суб- и сверхкритических флюидов в роли экстрагентов и растворителей в процессах выделения, разделения, очистки и фракционирования» /3/. При этом решаются проблемы создания перспективных энергосберегающих и малоотходных технологий.
Состояния веществ, находящихся при одинаковых
Уравнения типа (2) и (3) получаются в случае, если ограничиться рассмотрением только парных взаимодействий между молекулами, т.е. в группах по две молекулы. Поэтому эти уравнения применимы в области не очень высоких давлений.
С повышением давления необходимо учитывать образование устойчивых молекулярных образований из трех, четырех и более молекул, распад которых возможен только при подводе энергии извне, т.е. при нагревании. Такой газ можно рассматривать как «смесь» нескольких газов, частицами которых являются одиночные, двойные, тройные и т.д. группы молекул.
Уравнение состояния реальных газов формально можно записать в виде:
где z коэффициент сжимаемости (для идеальных газов z = 1) можно представить в виде вириального уравнения, учитывающего и взаимодействия более высокого порядка:
Правую часть этого уравнения можно рассматривать как разложение в ряд коэффициента z по степеням плотности
Второй вириальный коэффициент может быть определен по значениям потенциальной энергии взаимодействия силам притяжения и отталкивания двух молекул
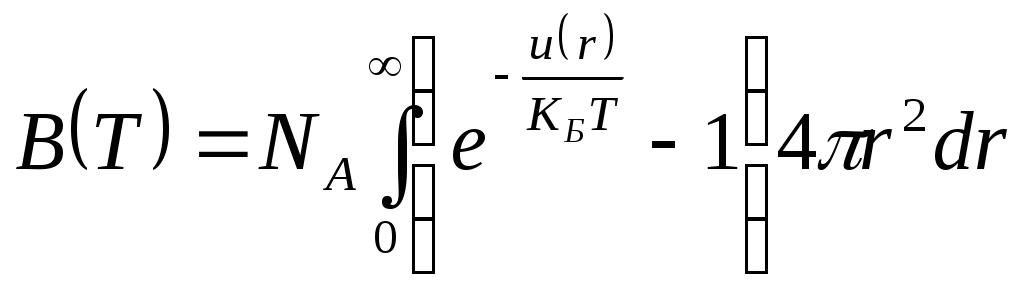 , (6)
, (6)где NA число Авогадро, NA = 6,0221026
КБ постоянная Больцмана, КБ = 1,3810-23
кстати
Определение последующих вириальных коэффициентов для газов достаточно большой плотности облегчается при наличии экспериментально полученных данных по теплофизическим свойствам этих газов (теплоемкость, вязкость, теплопроводность и т.п.).
К

оэффициент неидеальности z может быть найден также по зависимости
Р
z
ис.1. z–диаграмма реального газа.
Рассчитанное значение
Точность расчетов в этом случае окажется такой же, как и по уравнению Ван-дер-Ваальса (2) или приведенному уравнению (3)
Опыт Эндрюса
Свойства реальных газов не только в количественном, но и в качественном отношении отличаются от свойств реальных газов. Теория идеальных газов не может объяснить фазовые превращения газа и жидкости, она не может установить границы области фазовых переходов, параметры критического состояния.
В 1869 г. английский физик Эндрюс впервые на основании проведенных им экспериментов по изотермическому сжатию СО2 построил pv-диаграмму для реального газа и показал на ней характерные граничные линии и области состояний.
Р
2”
2’
2
Рис.2. pv-диаграмма реальных газов
р
v
4”
4’
4
1 ”
1’
1

р
анее было известно, что одни газы путем сжатия при комнатной температуре удается перевести в жидкое состояние, другие нет. Не было объяснения этому явлению.
П
v
4”
4’
4
1”
1’
1
3”
3’
3
2”
2’
2
роследить за поведением газа в процессе изотермического (
В точке 3 процесс конденсации завершается.
Кривая 3-4 соответствует процессу сжатия жидкой фазы при
Исследуя зависимость vот р на разных изотермах t, t’, t” и т.д., Эндрюс установил, что чем выше температура, тем меньше разница между удельными объемами сухого насыщенного пара
, x = 1), сближаются соответственно с точками 3,
х =
где
Разность удельных объемов
Таким образом, для реального газа в pv-диаграмме можно выделить три характерные области:
-
область жидкого состояния – расположена левее кривой х = 0 (БК),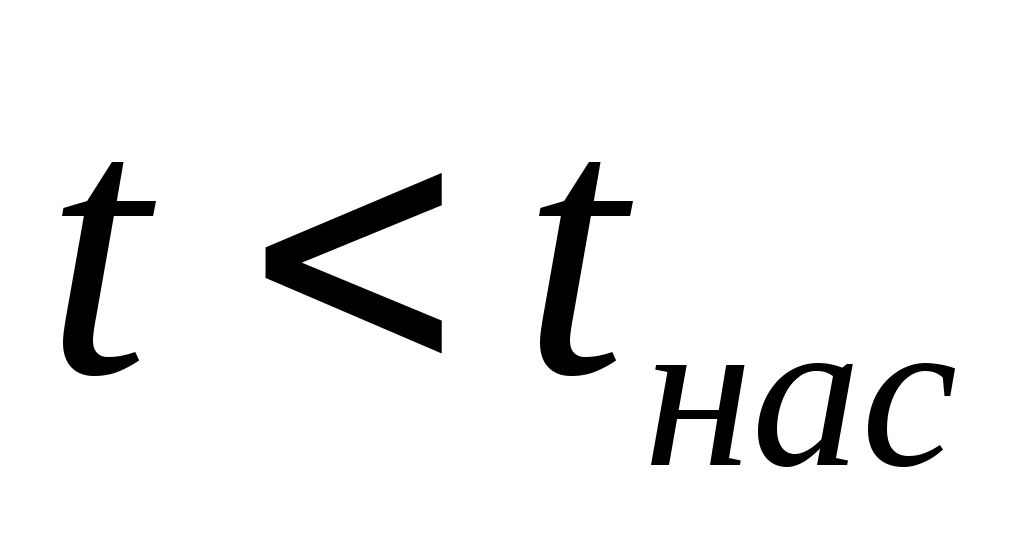 ;
; -
область двухфазных состояний – влажного насыщенного пара, расположенную между линиями х = 0 и х = 1 (между БК и АК),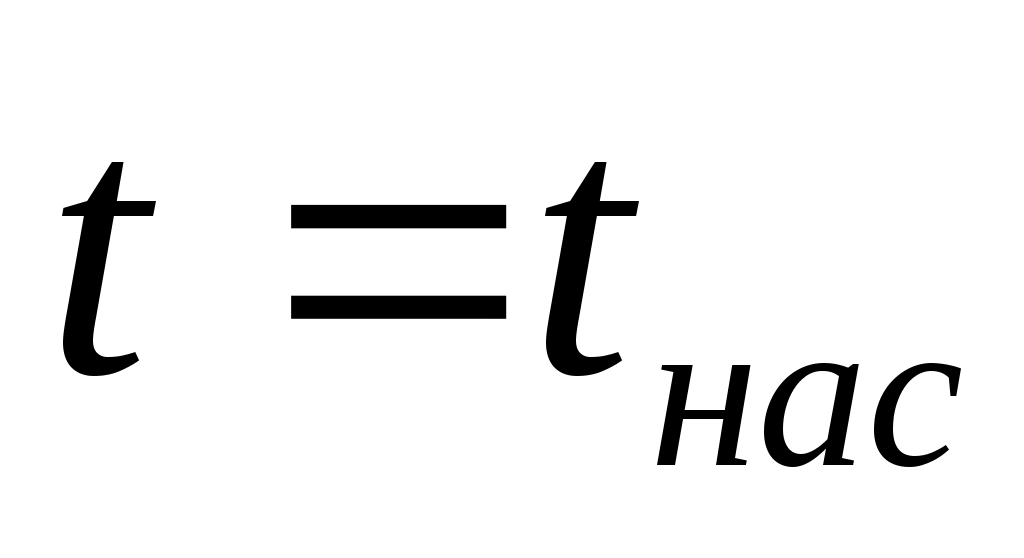 ;
; -
область перегретого пара, расположенную правее кривой х = 1 (АК),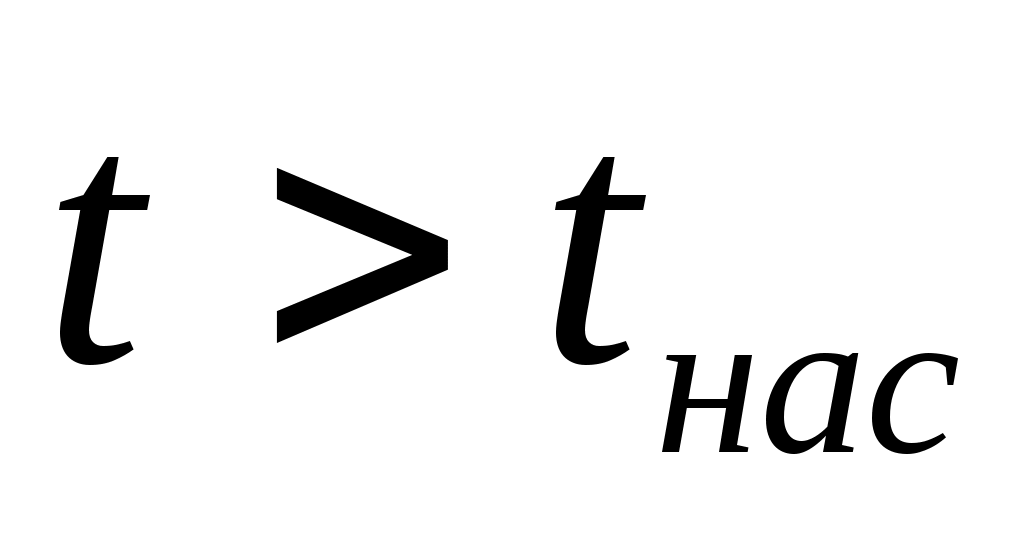 .
.
Нетрудно видеть, что при
В таблице 1 приведены критические параметры некоторых реальных газов.
Таблица 1
| Параметры | Н2 | N2 | CO2 | O2 | H2O | Hg |
| tкр., С | -239,9 | -147,0 | 31,05 | 118,4 | 374,15 | 1480 |
| ркр., МПа | 1,293 | 3,39 | 7,837 | 5,07 | 22,13 | 147,0 |
| vкр., м3/кг | 0,0323 | 0,00322 | 0,002137 | 0,00233 | 0,00326 | |
Вещество в критическом состоянии имеет ряд особенностей. Критическая изотерма tкр. в критической точке К имеет горизонтальную касательную и перегиб, т.е.
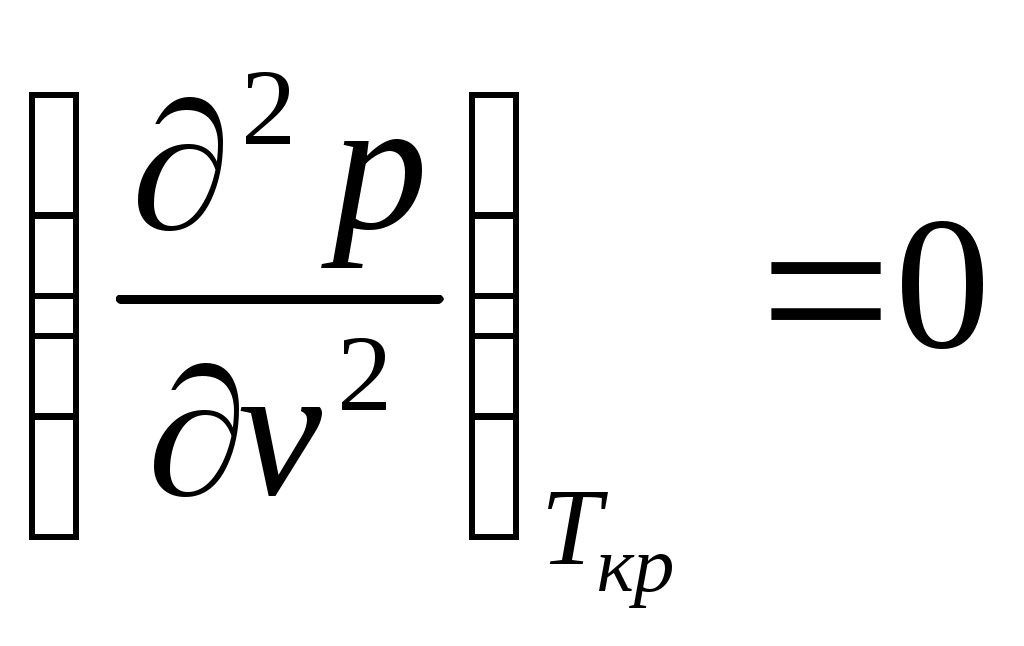 . (7)
. (7)Вблизи этой точки наблюдается скачек теплоемкости
Особые свойства веществ в критической и околокритической областях состояния в настоящее время уже находят применение в пищевой, фармацевтической, парфюмерной, химической, нефте- и углеперерабатывающей отраслях промышленности, в решении экологических проблем. В частности, «предложено использование суб- и сверхкритических флюидов в роли экстрагентов и растворителей в процессах выделения, разделения, очистки и фракционирования» /3/. При этом решаются проблемы создания перспективных энергосберегающих и малоотходных технологий.