Файл: Алгебра 1 семестр.pdf

59

ТЕОРИЯЛЫҚ СҰРАҚТАР 

•

Cызықты  тəуелді  вектолар  деп  қандай  векторларды 

айтамыз? 

•

Векторлық кеңістіктің өлшемі мен базисі деп нені айтамыз? 

•

Сызықты түрлендіру деп нені айтамыз? 

•

Сызықты  түрлендірудің  сипаттамалық  саны  мен  өзіндік 
векторын қалай табады?  

60

ТӨРТІНШІ ЛЕКЦИЯ 

АНАЛИТИКАЛЫҚ ГЕОМЕТРИЯ 

Аналитикалық геометрияның қарапайым есептері 

 1.  Екі  нүкте  ара  қашықтығы.  Жазықтықта 

)

,

(

1

1

y

x

A

  жəне 

)

,

(

2

2

y

x

B

 екі нүкте берілсін. Осы екі нүкте ара қашықтығын, немесе 

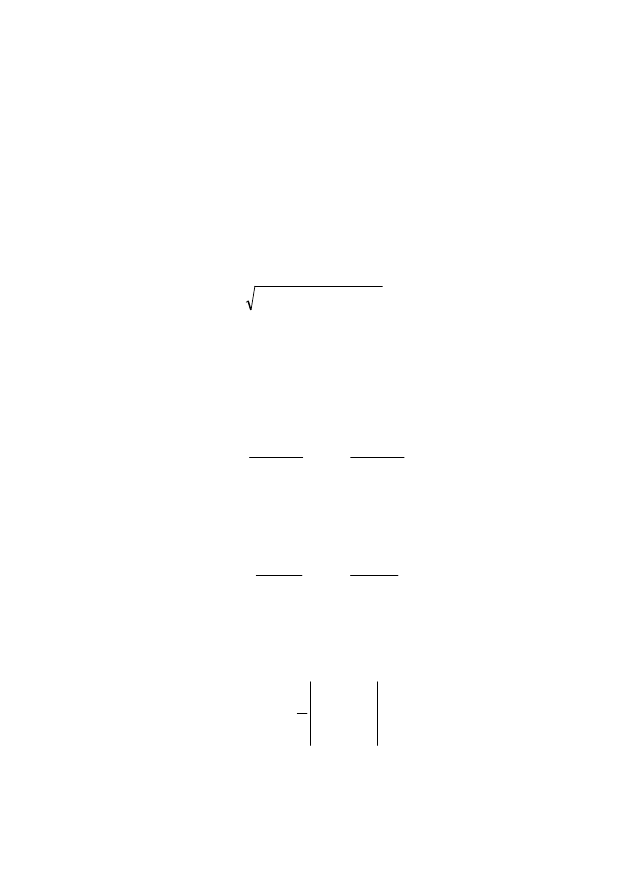
АВ кесіндісінің ұзындығын, мына формуламен есептейді: 

(

) (

)

2

1

2

2

1

2

y

y

x

x

d

−

+

−

=

. 

2.  Кесіндіні  берілген  қатынаста  бөлу.  Жазықтықта 

)

,

(

1

1

y

x

A

жəне 

)

,

(

2

2

y

x

B

  екі  нүкте  берілсін.  АВ  кесіндісін  АМ:МВ=

λ

болатындай қатынаспен бөлетін  М(х,у) нүктесінің координаталары 
мынадай формуламен есептелінеді: 

λ

λ

+

+

=

1

2

1

x

x

x

,   

λ

λ

+

+

=

1

2

1

y

y

y

. 

Дербес  жағдайда,  АВ  кесіндісін  тең  екіге  бөлу  керек  болса, 

яғни 

λ

=1:1=1, формула былай түрленеді: 

2

2

1

x

x

x

+

=

,   

2

2

1

y

y

y

+

=

. 

3. 

Үшбұрыш  ауданы.  Жазықтықта  төбелері 

)

,

(

1

1

y

x

A

, 

)

,

(

2

2

y

x

B

,

)

,

(

3

3

y

x

С

болатын 

үшбұрыш 

ауданы 

мынадай 

формуламен есептелінеді: 

1

1

1

2

1

3

3

2

2

1

1

y

x

y

x

y

x

S

±

=

∆

. 

61

B 

 A 

0

)

,

(

=

y

x

F

2

y

1

y

2

x

1

x

x

y

ЖАЗЫҚТЫҚТАҒЫ СЫЗЫҚ ТЕҢДЕУІ 

  Тік  бұрышты  координат 

жүйесінде, 

қандай 

да 

бір  

сызық берілсін. 

x жəне у айнымалыларды 

байланыстыратын мынадай  

F(x, y)=0   (1) 

теңдеу қарастырайық.  
 

Теңдеулерге мысал келтірсек:  
 

x - 5y – 2 = 0,   x

2

+y

2 

– 16 = 0. 

Аналитикалық  геометрияның  ең  басты  ұғымы  сызық 

теңдеуі болып табылады.  

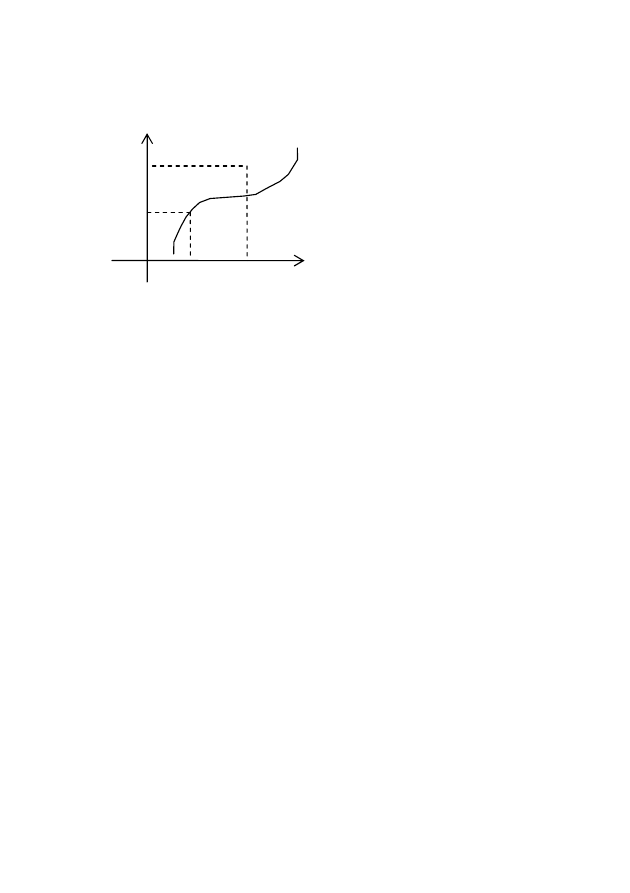
Анықтама.  Егер сызық бойында жатқан кез келген  нүкте 

координаталары  (1)  теңдеуді  қанағаттандырып,  одан  тыс 
жатқан бірде-бір нүкте оны қанағаттандырмаса, онда (1) теңдеу 
берілген сызықтың теңдеуі деп аталады. 

Суретте 

)

,

(

1

1

y

x

A

  нүктесі  сызық  бойында  жатқандықтан, 

оның координаталары (1) теңдеуді тепе теңдікке айналдырады 

0

)

,

(

1

1

≡

y

x

F

, 

ал 

)

,

(

2

2

y

x

B

  нүктесі  сызықтан  тысқары  жатқандықтан,  оның 

координаталары (1) теңдеуді қанағаттандырмайды  

0

)

,

(

2

2

≠

y

x

F

. 

Сызық  теңдеуі  ұғымы  геометриялық  есептерді  алгебралық 

тəсілдермен  шығаруға  мүмкіндік  береді.  Мысалы,    x-y-2=0,     
x

2

+y

2

-16=0  теңдеулерімен  анықталатын  сызықтардың  қилысу 

нүктесін  табу,  осы  теңдеулерден  тұратын  жүйені  шешуге,  яғни 
алгебралық есепті шешуге келтіріледі. 

62

0

B

y

x

M

K

α

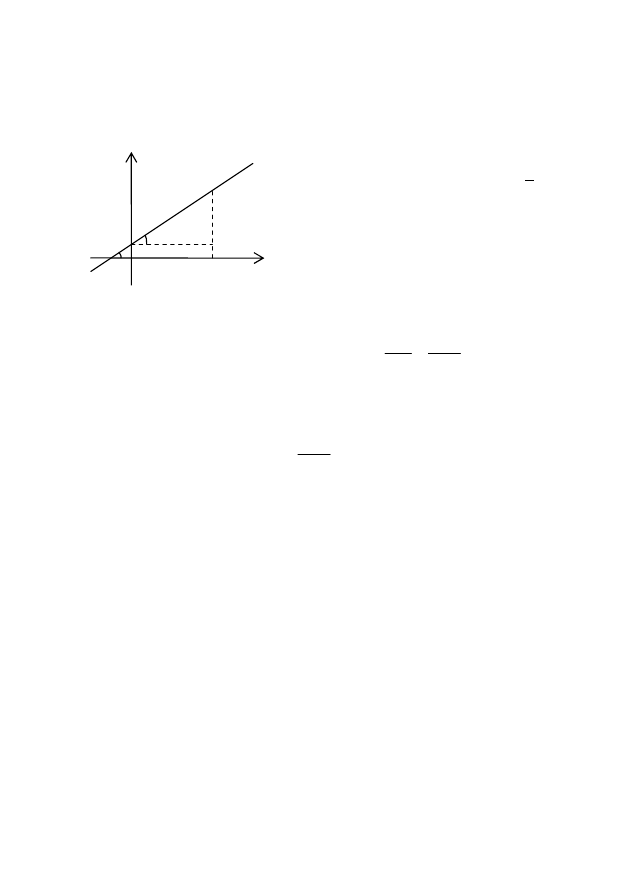
1-сурет 

ТҮЗУДІҢ ТҮРЛІ ТЕҢДЕУЛЕРІ 

       Жазықтықтағы    түзу  (1-
сурет)  Оу  осін  В(0;b)  нүктесінде 

қиып,    Ох  осімен   

α

(0<

α

<

2

π

)  

бұрыш    жасасын.  Түзу  бойынан  
қандай  да  бір  М(х,у)  нүкте 
алайық. 

Түзудің 

Ох 

осімен 

жасаған 

α

бұрышының 

тангенсін    ВМК  үшбұрышынан 
табамыз: 
 

x

b

y

KB

MK

tg

−

=

=

α

      (1) 

k

tg

=

α

 деп белгілеп, түзудің бұрыштық коэффициенті деп атау 

қабылданған. Сонымен: 

x

b

y

k

−

=

. 

Осы қатынастан у-ті тапсақ: 
 

y=kx+b                     (2) 

Түзу  бойында  жатқан  кез  келген  нүктенің  координатасы  (2) 
теңдеуді  қанағаттандырады  да  түзуден  тыс  жатқан  нүктелер  бұл 
теңдеуді қанағаттандырмайды.  
 

(2)  теңдеу  түзудің  бұрыштық  коэффициентімен  берілген 

теңдеуі деп аталады.  
 

Дербес жағдайларын қарастырайық. 

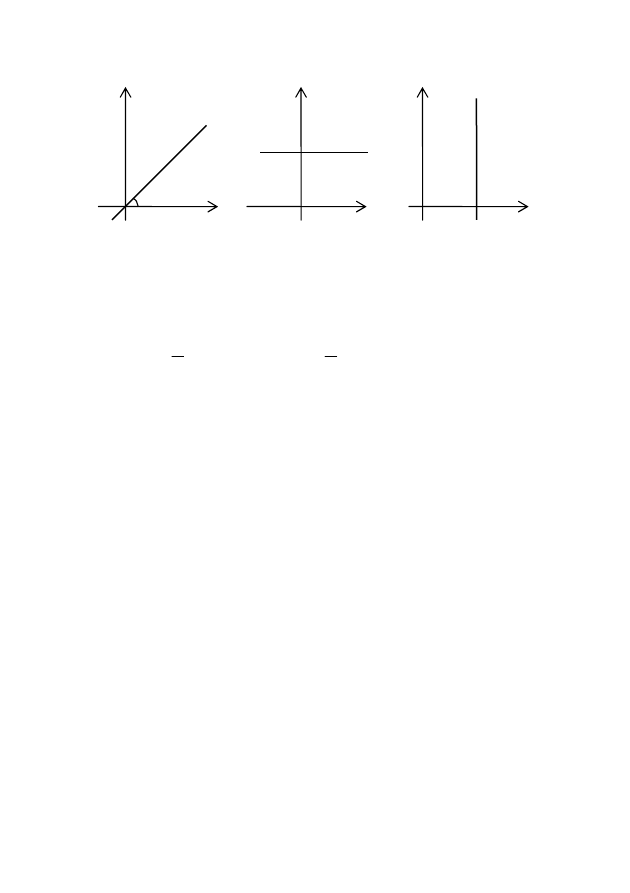
1.  Түзудің  бұрыштық  коэффициентімен  берілген  теңдеуіндегі  b=0 
болсын.  Онда  түзу  теңдеуі    y=kx  түрге  келеді  де,  түзу  координат 
басынан өтеді (2-сурет) 

63

2.  Егер 

0

=

α

  болса,  онда 

0

=

α

tg

  болады  да,  түзу  теңдеуі  y=b 

түрге  келеді  де,  түзу  Ох  осіне  параллель  болады  (3-сурет).  Ал  Ох 
осінің теңдеуі  y=0  болады. 

3.  Егер 

2

π

α

=

  болса,  онда 

2

π

tg

k

=

  мəні  болмайды,  түзу  Ох  осіне 

перпендикуляр болады. Айталық түзу Ох осінен а тең кесінді қиып 
өтеді, сонда түзу теңдеуі х=а түрде болады (4-сурет). Ал Оу осінің 
теңдеуі  х=0  болады. 
 

Мынадай теорема айтуға болады. 

Теорема.  Тік  бұрышты  координаталар  жүйесінде  кез 

келген түзу бірінші ретті теңдеумен беріледі  
 

Ах+Ву+С=0                                 (3) 

Жəне керісінше, (3) теңдеу (А, В, С коэффициенттердің бəрі бір 
мезгілде 

нолге 

тең 

болмаған 

кезде) 

тік 

бұрышты 

координаталар жүйесінде қандай да бір түзуді анықтайды. 
 

(3) теңдеуді əдетте түзудің жалпы теңдеуі деп атайды. 
 
Берілген бағыт жəне берілген нүкте арқылы өткен түзу 

теңдеуі. Көп жағдайда түзу теңдеуін оның бойында жатқан белгілі   

)

,

(

1

1

1

y

x

M

  нүкте  мен  k  бұрыштық  коэффициенті  арқылы  жазу 

керек болады (5-сурет).  

y

x=a 

y

0

=

y

b

y

=

b

a

0

0

0

y

α

x

x

x

2-сурет                          3-сурет                      4-сурет