Добавлен: 02.02.2019
Просмотров: 5530
Скачиваний: 25

9
Мысалы,
−
=
1
7
3
0
1
2
A
матрицасы
мен
−
=
5
0
2
3
1
4
0
2
1
B
матрицасын көбейтейік. Бірінші матрица үш тік жолдан, ал екінші
матрица үш жатық жолдан тұрғандықтан бұл матрицаларды
көбейтуге болады. Көбейтінді матрицаның өлшемін анықтайық:
3
2
3
3
3
2
x
C
x
B
x
A
=
⋅
,
яғни,
=
23
22
21
13
12
11
3
2
c
c
c
c
c
c
C
x
. k=3 болғандықтан (1) формуланы
қолданғанда үш қосылғыш болады:
j
i
j
i
j
i
b
a
b
a
b
a
ij
c
3
3
2
2
1
1
+
+
=
,
3
,
2
,
1
,
3
,
2
,
1
=
=
j
i
.
11
с
элементін табу үшін формуладағы i=1, j=1 деп аламыз, сонда
6
2
0
4
1
1
2
31
13
21
12
11
11
11
=
⋅
+
⋅
+
⋅
=
+
+
=
b
a
b
a
b
a
c
,
яғни А матрицаның 1-жатық жол элементтерін В матрицаның 1-тік
жолының сəйкес элементтеріне көбейтіп қостық. Осылай С
матрицаның барлық элементтері табылады:
C=
⋅
−
1
7
3
0
1
2
−
5
0
2
3
1
4
0
2
1
=
⋅
−
⋅
+
⋅
⋅
−
−
⋅
+
⋅
⋅
−
⋅
+
⋅
⋅
+
⋅
+
⋅
⋅
+
−
⋅
+
⋅
⋅
+
⋅
+
⋅
5
1
3
1
0
3
0
1
)
1
(
7
2
3
2
1
4
7
1
3
5
0
3
1
0
2
0
0
)
1
(
1
2
2
2
0
4
1
1
2
=
=
−
−
2
1
27
3
3
6
.

10
Қосу жəне көбейту амалдарының мынадай қасиеттері
бар:
1) A+B=B+A
5) (A+B)C=AC+BC
2) (A+B)+C=A+(B+C)
6)
λ
(AB)=(
λ
A)B=A(
λ
B)
3)
λ
(A+B)=
λ
A+
λ
B
7) A(BC)=(AB)C
4) A(B+C)=AB+AC
Бұл қасиеттер сандарға жасалатын амалдар қасиеттеріне
ұқсас. Енді матрицаның өзіндік ерекшелігіне байланысты
қасиеттерін қарастырайық.
8) Біріншіден, екі матрицаның АВ көбейтіндісі болғанмен ВА
көбейтіндісі болмауы мүмкін. Мысалы,
3
3
3
2
x
x
B
A
⋅
көбейтіндісі бар,
бірақ
3
2
3
3
x
x
A
B
⋅
көбейтіндісі жоқ, себебі бірінші матрицаның тік
жолдар саны екінші матрицаның жатық жолдар санына тең емес;
екіншіден, АВ жəне ВА көбейтінділері бар болғанмен, олардың
өлшемдері əртүрлі болуы мүмкін. Мысалы,
2
3
3
2
x
x
B
A
⋅
жəне
3
2
2
3
x
x
A
B
⋅
көбейтінділер бар, бірақ өлшемдері əртүрлі:
2
2
2
3
3
2
x
x
x
C
B
A
=
⋅
,
3
3
3
2
2
3
x
x
x
C
A
B
=
⋅
;
үшіншіден, АВ жəне ВА көбетінділер бар жəне олардың өлшемдері
бірдей болғанмен, жалпы жағыдайда, көбейтудің коммутативті
заңы орындалмайды, яғни АВ
≠
BA.
Мысал.
−
=
4
3
2
1
A
мен
−
=
1
5
0
2
B
матрицалары
берілген. АВ жəне ВА көбейтінділерін табау керек.
Шешуі. Берілген матрицалар өлшемдері 2х2 квадрат
матрицалар, оларды көбейтуге болады:
=
+
+
+
+
−
=
−
⋅
−
=
⋅
4
26
2
8
4
0
20
6
2
0
10
2
1
5
0
2
4
3
2
1
B
A
.
−
−
=
+
−
+
−
+
−
=
−
⋅
−
=
⋅
14
2
4
2
4
10
3
5
0
4
0
2
4
3
2
1
1
5
0
2
A
B
.

11
Көріп отырғанымыздай АВ
≠
BA.
9) А-квадрат матрица болса, онда мына теңдік орындалады:
АЕ = ЕА = А.
4. Матрицаны транспонерлеу. Қандай да бір А
матрицасының жатық жолын сəйкес тік жол етіп жазғаннан пайда
болған матрицаны берілген матрицаның транспонерленген
матрицасы деп атайды да,
A
′
деп белгілейді. Берілген
матрицаның
өлшемі
mxn
болса,
оның
транспонерленген
матрицасының өлшемі nxm болады. Мысалы,
−
=
1
7
3
0
1
2
3
2x
A
матрицасының бірінші жатық жолын бірінші тік жол етіп, ал
екінші жатық жолын екінші тік жол етіп жазып оның
транспонерленген матрицасын
−
=
′
1
0
7
1
3
2
2
3x
A
аламыз.
АНЫҚТАУЫШ. МИНОР ЖƏНЕ АЛГЕБРАЛЫҚ
ТОЛЫҚТАУЫШ
Квадрат матрицаны сипаттауға қажетті анықтауыш ұғымын
енгізейік.
Екінші ретті матрицаның
=
22
21
12
11
a
a
a
a
A
анықтауышы
немесе екінші ретті анықтауыш деп мынадай санды айтады:
21
12
22
11
22
21
12
11
a
a
a
a
a
a
a
a
A
−
=
=
=
∆
Мысалы,
1
2
3
5
матрицаның анықтауышын есептейік:
12
1
2
3
1
5
1
2
3
5
−
=
⋅
−
⋅
=
.
Ал үшінші ретті матрицаға
=
33
32
31
23
22
21
13
12
11
a
a
a
a
a
a
a
a
a
A
үшінші ретті
анықтауыш сəйкес келеді:
11
32
23
33
21
12
31
22
13
13
32
21
31
23
12
33
22
11
33
32
31
23
22
21
13
12
11
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
A
−
−
−
−
+
+
=
=
=
∆
.
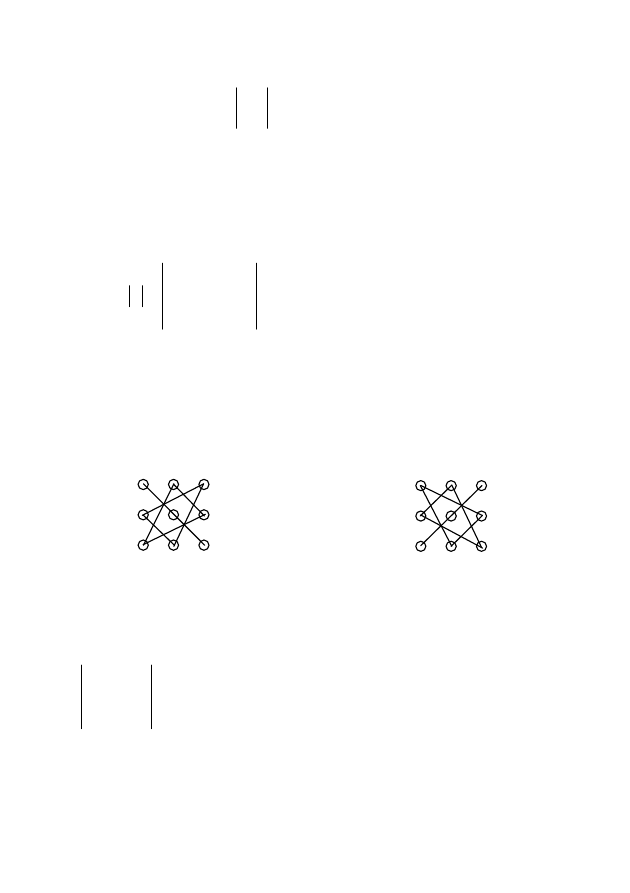
Бұл анықтауыштың есептелуін үшбұрыш ережесі немесе Саррус
ережесімен оңай есте сақтауға болады. Бұл ереже бойынша
алғашқы оң таңбалы үш қосылғыш 1-схема, ал кейінгі теріс
таңбалы үш қосылғыш 2-схемамен есептелінеді.
33
32
31
23
22
21
13
12
11
a
a
a
a
a
a
a
a
a
1-схема 2-схема
Мысалы, мынадай үшінші ретті анықтауышты есептейік:
55
0
15
8
60
0
2
1
)
3
(
0
)
1
(
5
3
1
2
4
4
)
3
(
5
1
0
3
)
1
(
2
1
1
3
1
0
2
5
4
3
1
−
=
+
+
−
−
+
−
=
=
⋅
−
⋅
−
−
⋅
⋅
−
⋅
⋅
−
⋅
−
⋅
+
⋅
⋅
+
−
⋅
⋅
=
−
−

13
Реті үштен көп болатын анықтауыштарды есептеу үшін
жаңа ұғымдар қажет болады.
Анықтама. n-ретті квадрат матрицаның
i
–жатық
жолы мен
j
–тік жолын сызып тастағаннан кейін пайда
болған (n–1)-ретті анықтауықты
ij
a
элементінің миноры деп
атайды жəне
ij
M
деп белгілейді.
Үшінші ретті марицаның
21
a
элементінің миноры мынадай
екінші ретті анықтауыш болады:
32
13
33
12
33
32
13
12
21
a
a
a
a
a
a
a
a
M
−
=
=
.
ij
a
элементінің
алгебралық
толықтауышы
деп
мынадай санды айтады:
ij
j
i
ij
M
A
+
−
=
)
1
(
Үшінші
ретті
марицаның
21
a
элементінің
алгебралық
толықтауышы мынадай сан:
21
21
1
2
21
)
1
(
M
M
A
−
=
−
=
+
Мысалы,
−
−
=
1
3
1
0
2
5
4
3
1
A
матрицасының бірінші жатық
жолдағы
элементтерінің
миноры
мен
алгебралық
толықтауыштарын есептейік:
1
11
=
a
,
2
)
3
(
0
)
1
(
2
1
3
0
2
11
−
=
−
⋅
−
−
⋅
=
−
−
=
M
,
2
)
1
(
11
1
1
11
−
=
−
=
+
M
A
,