Добавлен: 02.02.2019
Просмотров: 5532
Скачиваний: 25
64
0
B
A
y
x
2
y
1
y
2
x
1
x
7-сурет
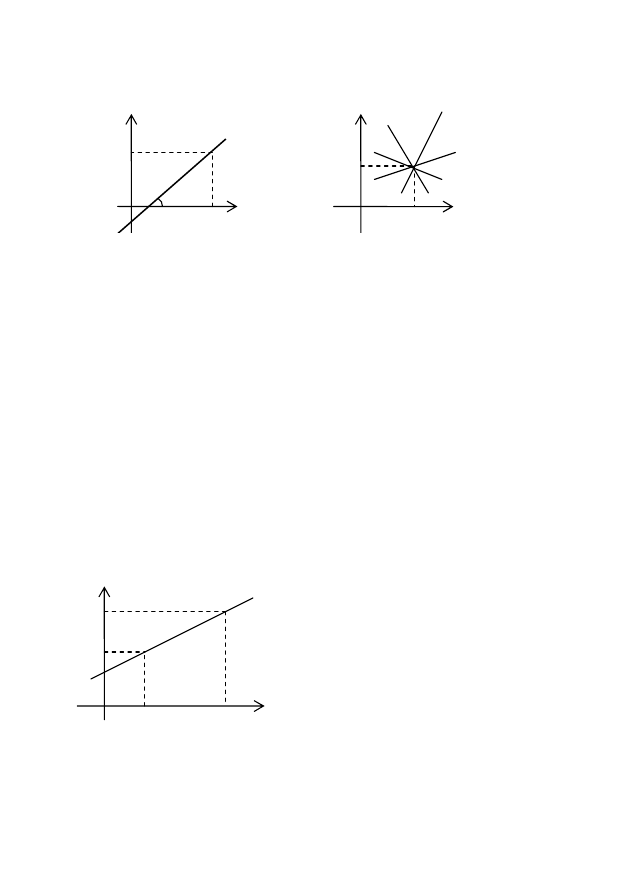
Түзу теңдеуін (2) түрінде жазайық, y=kx+b, мұндағы b
əзірше белгісіз. Түзу
)
,
(
1
1
1
y
x
M
нүктесі арқылы өтетіндіктен, нүкте
координатасы түзу теңдеуін қанағаттандыруы керек: y
1
=kx
1
+b.
Осы теңдіктен белгісіз b табылады, b = y
1
- kx
1.
Табылған мəнді
теңдеудегі орнына қойып, берілген бағыт жəне берілген нүкте
арқылы өткен түзу теңдеуін аламыз:
y =k(x – x
1
)+ y
1
(4)
Егер (4) теңдеудегі k ерікті мəн қабылдаса, онда теңдеу
)
,
(
1
1
1
y
x
M
нүктесі арқылы өтетін түзулер шоғының теңдеуін
анықтайды (6-сурет).
Берілген екі нүкте арқылы өткен түзу теңдеуі.
)
,
(
1
1
y
x
A
жəне
)
,
(
2
2
y
x
B
нүктелері берілсін. АВ түзуінің теңдеуін жазу үшін
А нүктесі арқылы өткен түзулер
шоғының теңдеуін жазамыз:
y =k(x – x
1
)+ y
1.
АВ
түзуі
)
,
(
2
2
y
x
B
нүктесі
арқылы
өтетіндіктен,
нүкте
координатасы
түзу
теңдеуін қанағаттандыруы керек:
y
2
=k(x
2
– x
1
)+ y
1.
Осы теңдіктен
белгісіз
k
табылады,
0
0
α
0
y
0
M
0
x
0
M
0
y
0
x
x
x
y
y
5-сурет 6-сурет
65
a
b
A
0
B
y
x
8-сурет
ϕ
2
α
1
α
0
y
x
9-сурет
1
2
1
2
x
x
y
y
k
−
−
=
. Табылған мəнді теңдеудегі орнына қойып, берілген
екі нүкте арқылы өткен түзу теңдеуін аламыз:
1
2
1
1
2
1
x
x
x
x
y
y
y
y
−
−
=
−
−
(5)
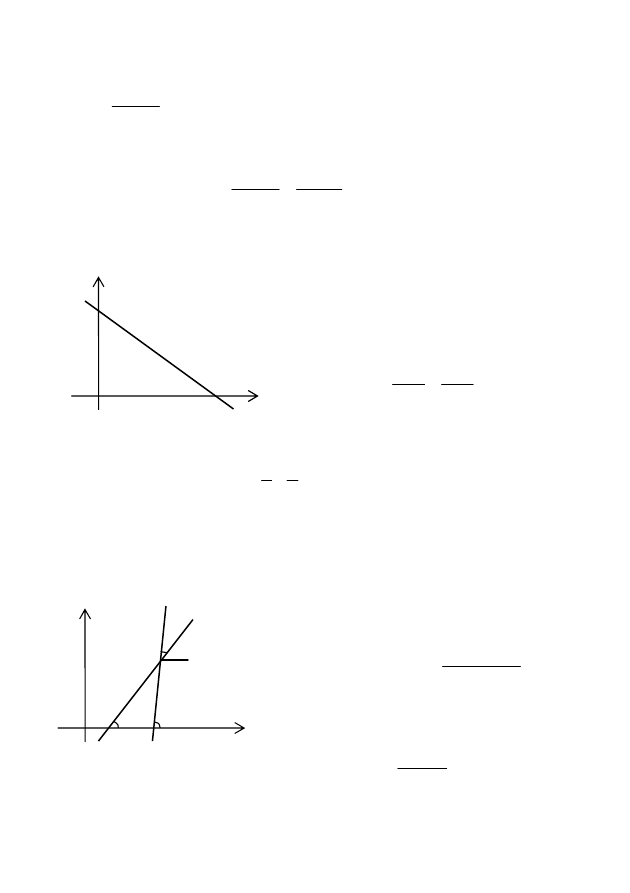
Түзудің “кесіндідегі” теңдеуі. Түзу Ох осінен а-ға тең, Оу
осінен b-ға тең кесінді қиып өтсін (8-
сурет). Түзу А(а;0) жəне В(0;b)
нүктелері арқылы өтеді деп, (5)
теңдеуді қолданайық. Сонда түзу
теңдеуі мынадай түрде жазылады:
a
a
x
b
y
−
−
=
−
−
0
0
0
Енді
ықшамдасақ,
түзудің
“кесіндідегі” теңдеуін аламыз:
1
=
+
b
y
a
x
(6)
Суреттен көрініп тұрғандай
1
2
α
α
ϕ
−
=
.
Осыдан
2
1
1
2
1
2
1
)
(
α
α
α
α
α
α
ϕ
tg
tg
tg
tg
tg
tg
+
−
=
−
=
немесе
2
1
1
2
1
k
k
k
k
tg
+
−
==
ϕ
(7)
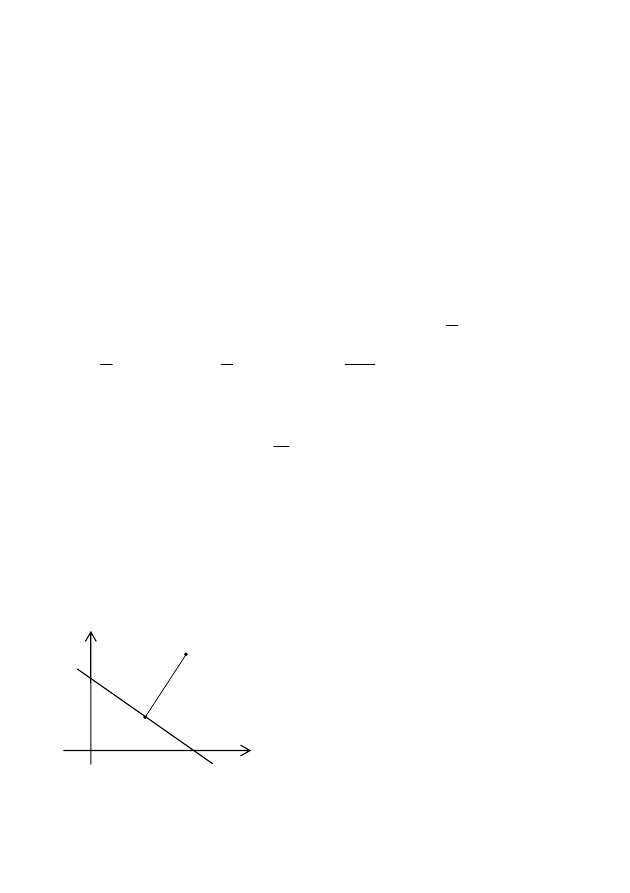
Екі түзу арасындағы бұрыш. Екі түзу
берілсін:
y=k
1
x+b
1
, y=k
2
x+b
2
. Мұндағы
1
1
α
tg
k
=
,
2
2
α
tg
k
=
. Екі түзу
арасындағы
ϕ
бұрышты табу керек (9-сурет).
66
x
)
,
(
0
0
y
x
M
)
,
(
1
1
y
x
N
0
y
10-сурет
(7) формула берілген екі түзу арасындағы бұрышты анықтайды. Ал
екінші бұрыш
ϕ
π
−
тең болады.
Екі түзудің параллелдік жəне перпендикулярлық
шарты. Егер екі түзу параллель болса, онда
ϕ
=0 болады да
tg
ϕ
=0. Бұл жағдайда (7) формула мынадай түрге келеді:
k
2
– k
1
= 0. Осыдан екі түзудің параллелдік шарты шығады:
k
2
= k
1
, (8)
яғни екі түзудің бұрыштық коэффициенттері тең болса, ол түзулер
параллель болады жəне керісінше.
Егер екі түзу перпендикуляр болса, онда
2
π
ϕ
=
болады да,
1
2
2
α
π
α
+
=
,
1
1
1
2
1
)
2
(
α
α
α
π
α
tg
ctg
tg
tg
−
=
=
+
=
. Осыдан екі түзудің
перпендикулярлық шарты шығады:
k
2
=
1
1
k
−
, (9)
яғни екі түзудің бұрыштық коэффициенттері мəндері бойынша
кері, таңбалары бойынша қарама-қарсы болса, ол түзулер
перпендикуляр болады жəне керісінше.
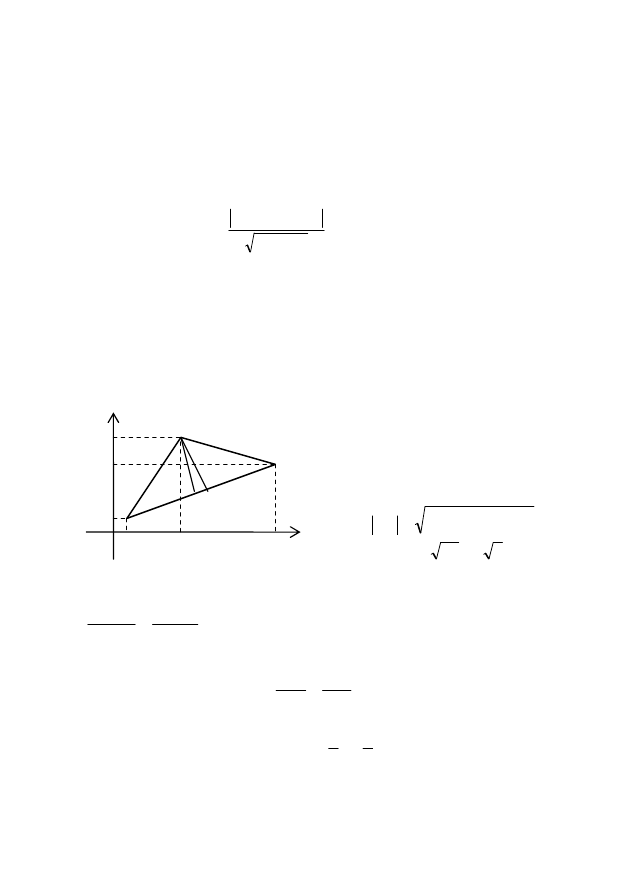
Нүктеден түзуге дейінгі қашықтық. Тік бұрышты
координаталар жүйесінде қандай да бір түзу Ах+Ву+С=0 жəне
түзуден тыс жатқан нүкте М(х
0
,у
0
) берілсін (10-сурет).
Нүктеден
түзуге
дейінгі
қашықтық
деп
нүктеден
түзуге
түсірілген
перпендикуляр
ұзындығын
айтамыз. Суретте ол d=MN.
Осы ара қашықтықты табу
үшін: а) Берілген түзуге
перпендикуляр жəне М(х
0
,у
0
)
нүктесі арқылы өтетін түзу
67
Y
X
Е
D
B
C
A
11-сурет
теңдеуін тауып аламыз; б) Берілген түзу мен MN түзулерінің
теңдеуін жүйе етіп шешіп, олардың қилысу нүктесі N
)
,
(
1
1
y
x
табамыз; в) екі нүктенің ара қашықтығын есептейтін формула
көмегімен d=MN ара қашықтықты есептейміз. Нəтижесінде
мынадай формула алынады:
2
2
0
0
B
A
C
By
Ax
d
+
+
+
=
(10)
Мысал. Төбелері А(1;1), В(7;4), С(4;5) болатын үшбұрыштың
а) АВ қабырғасының ұзындығын;
б) АВ жəне АС түзулерінің теңдеуін;
в) А ішкі бұрышын;
г) С төбесінен жүргізілген биіктік пен медиана теңдеулерін;
д) С төбесінен АВ қабырғасына дейінгі қашықтықты табу
керек.
Шешуі. а) Кесінді ұзындығын
есептейтін формула бойынша АВ
қабырғасының
ұзындығын
есептейміз:
(
) (
)
5
3
45
2
1
4
2
1
7
=
=
=
−
+
−
=
AB
б) АВ түзуінің теңдеуін
1
2
1
1
2
1
x
x
x
x
y
y
y
y
−
−
=
−
−
формуланы пайдаланып табамыз. Мұндағы
)
,
(
1
1
y
x
жəне
)
,
(
2
2
y
x
нүктелер А жəне В нүктелерінің
координаталары болады:
1
7
1
1
4
1
−
−
=
−
−
x
y
, ықшамдасақ,
2
1
2
1
+
=
x
y
теңдеуін аламыз.

68
Дəл осы жолмен АС түзуінің теңдеуін аламыз:
1
4
1
1
5
1
−
−
=
−
−
x
y
,
осыдан
3
1
3
4
−
=
x
y
.
в) А ішкі бұрышын есептеу үшін (7) формуланы пайдаланамыз.
Ол үшін АВ жəне АС түзулерінің коэффициенттерін алдыңғы
пункттегі теңдеулерінен аламыз да,
2
1
=
AB
k
,
3
4
=
AC
k
, (7) формулаға қоямыз:
5
,
0
3
4
2
1
1
2
1
3
4
=
⋅
+
−
==
tgА
,
осыдан
5
,
0
arctg
A
=
∠
.
г) С төбесінен жүргізілген биіктікті СD дейік. СD теңдеуін
жазу үшін y =k(x – x
1
)+ y
1
теңдеуді пайдаланамыз.
)
,
(
1
1
y
x
нүктенің орнына С нүктесінің координатасын қойсақ осы нүкте
арқылы өтетін түзулер шоғының теңдеуін аламыз: y =k(x -4)+ 5.
Осы шоқтан
АВ түзуіне перпендикуляр түзу теңдеуін таңдап алу
үшін СD биіктіктің АВ түзуге перпендикуляр болатынын ескеріп
2
1
−
=
−
=
AB
k
k
табылады да, түзулер шоғы теңдеуіндегі орнына
қойылады:
y =-2(x -4)+ 5
.
Ықшамдап СD биіктік теңдеуін аламыз,
y =-2x+13.
СЕ медиана теңдеулерін жазу үшін АВ кесіндісінің
ортасында жатқан Е нүктесінің координаталарын табамыз:
4
2
7
1
2
=
+
=
+
=
B
A
E
x
x
x
,
5
,
2
2
4
1
2
=
+
=
+
=
B
A
E
y
y
y
, Е=(4; 2,5).
Екі нүкте арқылы өткен түзу теңдеуін пайдаланып медиана
теңдеуін аламыз:
4
4
4
5
5
,
2
5
−
−
=
−
−
x
y
,