определена тогда и только тогда, когда определены все функции и функция определена на наборе . Операцию суперпозиции обозначают: .

Операция рекурсии (точнее: примитивной рекурсии). Пусть заданы -местная функция и -местная функция . Определим -местную функцию индуктивным образом с помощью соотношений:

;

.

Ясно, что данные соотношения однозначно определяют функцию . считается определённой в том и только в том случае, когда определены и при . Значит, если неопределено, то и неопределено при . Про функцию говорят, что она получена рекурсией из функций

---

и , и обозначают: .

Операция минимизации. Пусть задана -местная функция . Зафиксируем набор и рассмотрим уравнение относительно :

.

Будем решать данное уравнение, вычисляя последовательно , , и т.д. и сравнивая с . Наименьшее , для которого выполнено уравнение обозначим . При этом считаем, что определено, если определено при всех . В противном случае считаем, что неопределено. Значение есть функция от переменных , про которую говорят, что она получена из минимизацией и обозначают: .

Функция называется частично-рекурсивной, если она может быть получена из базисных функций

---

, , применением конечного числа раз операций суперпозиции, рекурсии и минимизации.

Какая же связь между частично рекурсивными функциями и теорией алгоритмов? Эту связь устанавливает «тезис Чёрча» ¹, для формулировки которого введём понятие вычислимой функции.

Определение ². Функция называется алгоритмически вычислимой, если существует алгоритм нахождения значения функции при любом допустимом значении аргумента.

Очевидно, что функции , и алгоритмически вычислимы. Можно доказать, что операции суперпозиции, рекурсии и минимизации сохраняют свойство вычислимости ³. Значит, все частично рекурсивные функции вычислимы. Тезис Чёрча утверждает, что класс алгоритмически вычислимых функций совпадает с классом всех частично рекурсивных функций. То есть выполняется и обратное включение: все вычислимые функции частично рекурсивны. Принятие данного тезиса позволяет истолковывать доказательство, что некоторая функция не является частично рекурсивной, как доказательство отсутствия алгоритма вычисления ее значений.

Аппарат частично рекурсивных функций позволяет исследовать общие алгоритмические проблемы. Для этого используется метод характеристик. Он заключается в следующем. По конкретной задаче строится соответствующая характеристическая функция, которая затем изучается на вычислимость. Вычислимость её позволяет утверждать разрешимость исходной проблемы. Пусть, например, стоит проблема разрешения предиката ⁴. То есть если задан -местный предикат , то необходимо указать алгоритм позволяющий получить значение предиката для каждого набора или доказать, что такого алгоритма нет. Составляем характеристическую функцию:

---

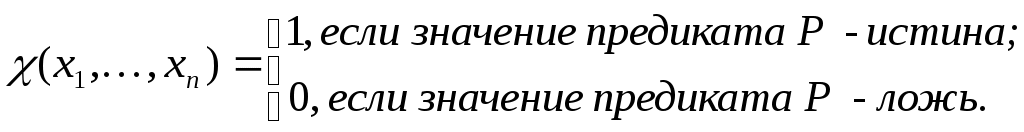
Теперь если функция не частично рекурсивна, то искомого алгоритма не существует. А доказательство частичной рекурсивности сразу даёт рекурсивный алгоритм разрешения предиката.

Аналогично теоретически можно получить рекурсивное решение любой разрешимой алгоритмической задачи. Однако практическая ценность этого метода невелика, так как доказательства часто неконструктивны, то есть показывают существование решения, но не содержат инструкций, как определить его явно. Требуется дополнительное исследование, нередко чрезвычайно трудоёмкое.

Таким образом, мы выяснили, что для любой алгоритмической задачи, допускающей решение, можно указать рекурсивный разрешающий алгоритм. То есть рекурсивные алгоритмы являются универсальным средством во всех науках использующих понятие алгоритм. С другой стороны из эквивалентности способов формализации алгоритмов по Тьюрингу и по Чёрчу следует важный вывод, что для каждого рекурсивного алгоритма можно указать итерационный, дающий тот же результат.

Метрическая теория.

В предыдущем пункте было показано, что любой алгоритм может быть представлен как в виде, содержащем рекурсию, так и не содержащем её. Тогда в каждом конкретном случае целесообразность использование на практике того или иного типа записи, обосновывается с использованием метрической теории алгоритмов, или теории сложности. Нужно отметить, что для многих практически важных задач лучшие оценки сложности дают алгоритмы, использующие рекурсию. Рассмотрим несколько примеров.

1.Умножение -разрядных двоичных чисел. Даны два -разрядных двоичных числа и требуется найти их произведение. «Наивный» алгоритм умножения «столбиком» требует битовых операций. Предложим рекурсивный алгоритм для данной задачи. Пусть и - два -битовых числа и пусть

---

, в противном случае дополняем числа слева нулями. Разобьем числа и на две равные части в виде , и будем рассматривать каждую часть как -разрядное двоичное число. Тогда произведение можно представить в виде



Равенство дает способ вычисления произведения с помощью четырех умножении -разрядных чисел и некоторого числа сложении и сдвигов (умножений на степень числа 2). Действительно, находим

,

где , , . Ясно, что операции сложения и сдвига имеют сложность .

Заметим, что и имеют, вообще говоря, разрядов. Тогда

запишем равенства , и, следовательно, . Произведение находится с помощью рекурсивного алгоритма на задачах размера

---

Смотрите также файлы

• Алексей Мазур, группа 20ф14.docx

• Разработка технологического процесса ремонта крышек люков полувагона со снятием с вагона.pdf

• 1 Культурноисторическая теория психического развития человека Л. С. Выготского.docx

• Дипломная работа Лавренова Михаила Владимировича Студента 4 курса 1 группы Научный.docx

• Министерство здравоохранения иркутской области областное государственное бюджетное профессиональное образовательное учреждение.pptx