Добавлен: 07.11.2023
Просмотров: 143
Скачиваний: 7
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Размер стека по умолчанию – 16 Кб, а максимальный размер – 64Кб. Если незавершенных рекурсивных вызовов слишком много (по ошибке в программе может возникнуть и бесконечной рекурсией), то система выдаст сообщение «Stack overflow» («Переполнение стека»). Это одна из самых распространённых ошибок при программировании рекурсивных алгоритмов. В первую очередь необходимо проверить рекурсию, используемую в программе, на наличие условия завершения (так называемой базовой задачи), чтобы убедиться в отсутствии бесконечной рекурсии. В других случаях есть смысл увеличить размер стека, используя меню «Options | Memory Sizes ”.
При необходимости можно манипулировать стеком с помощью директивы компилятора $M, содержащей три параметра. Размер стека определяется первым параметром директивы. Второй и третий ее параметры – нижняя и верхняя границы области динамически выделяемой памяти (кучи, heap). Однако нужно помнить, что эти установки будут действовать только для данной программы.
Сам рекурсивных вызов осуществляется по обычным синтаксическим правилам вызова подпрограмм.
Видим, что использование рекурсии стало простым и понятным. Это создаёт дополнительный стимул для активного её применения в практическом программировании.
Заключение.
По итогам разностороннего исследования рекурсивных алгоритмов можно сделать ряд важных и, надо сказать, приятных выводов.
Во-первых, рекурсивные алгоритмы есть универсальное средство решения разнообразных алгоритмических проблем. Показано, что любая разрешимая задача такого рода имеет рекурсивное решение, которое при этом отличается изяществом и простотой для восприятия человеком.
Во-вторых, рекурсивные алгоритмы часто имеют более низкую асимптотическую сложность, чем эквивалентные им итерационные. То есть теоретически они быстрее.
В-третьих, развитие современных программных средств сделало практическое использование рекурсии достаточно несложным делом, а новые концепции и технологии программирования преодолели проблему низкой эффективности рекурсивных программ, созданную необходимостью вызова большого количества подпроцедур.
Конечно, после всего вышесказанного не стоит считать рекурсивные алгоритмы панацеей от всех профессиональных болезней программиста. Но в то же время не стоит умалять их значения. Основное – это быстро и качественно найти решение стоящей задачи, и тут следует принимать во внимание и возможность применения рекурсивных алгоритмов.
Список использованной литературы.
-
Носов В.А. Основы теории алгоритмов и анализа их сложности. – М., 1992. -
Федер Е. Фракталы. – М.: Мир, 1991. -
Клейн М. Математика. Утрата неопределённости. – М.: Мир, 1987. -
Фиошин М.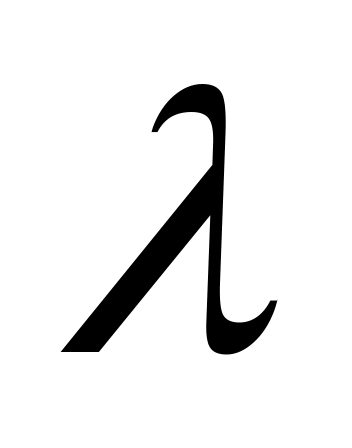
-исчисление. – М., 1990. -
Катленд Н. Вычислимость. Введение в теорию рекурсивных функций. – М., 1983. -
Емельченков Е.П., Емельченков В.Е. Вычислимость. Введение в теорию алгоритмов. – М., 2000. -
Глухов М.М. Математическая логика. – М., 1982. -
Мальцев А.И. Алгоритмы и рекурсивные функции. – М., 1965. -
Трахтенброт Б.А. Сложность алгоритмов и вычислений: спецкурс для студентов НГУ. – Новосибирск, 1967. -
Трахтенброт Б.А. Алгоритмы и вычислительные автоматы. – М., 1974. -
Успенский В.А., Семёнов А.Л. Теория алгоритмов: основные открытия и приложения. – М., 1987. -
Абрамов С.А. Математические построения и программирование. – М.: Наука, 1978. -
Кнут Д. Искусство программирования для ЭВМ. -
Шилдт Г. Работа с Турбо Паскалем. – М., 1990.
1 Федер Е. Фракталы. – М.: Мир, 1991.
1 Носов В.А. Основы теории алгоритмов и анализа их сложности. – М., 1992.
2 Клейн М. Математика. Утрата неопределённости. – М.: Мир, 1987.
3 Носов В.А. Основы теории алгоритмов и анализа их сложности. – М., 1992.
1 Фиошин М.
-исчисление. – М., 1990.2 Носов В.А. Основы теории алгоритмов и анализа их сложности. – М., 1992.
3 Там же.
1 Емельченков Е.П., Емельченков В.Е. Вычислимость. Введение в теорию алгоритмов. – М., 2000.
2 Носов В.А. Основы теории алгоритмов и анализа их сложности. – М., 1992.
3 Там же.
4 Глухов М.М. Математическая логика. – М., 1982.
1 Успенский В.А., Семёнов А.Л. Теория алгоритмов: основные открытия и приложения. – М., 1987.
2 Носов В.А. Основы теории алгоритмов и анализа их сложности. – М., 1992.
1 Там же.
2 Там же.
3 Там же.
1 Там же.
2 Там же.
1 Успенский В.А., Семёнов А.Л. Теория алгоритмов: основные открытия и приложения. – М., 1987.
1 Трахтенброт Б.А. Алгоритмы и вычислительные автоматы. – М., 1974.
1 Кнут Д. Искусство программирования для ЭВМ, т.3. – М.: Мир, 1994.
1 Кнут Д. Искусство программирования для ЭВМ, т.4.