Добавлен: 07.11.2023
Просмотров: 142
Скачиваний: 7
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
В некоторых случаях рекурсию для задачи размера
удаётся организовать только путем аддитивного уменьшения исходного размера задачи на некоторую константу 
. Сложность 
такого типа рекурсивных алгоритмов определяется рекуррентным соотношением вида
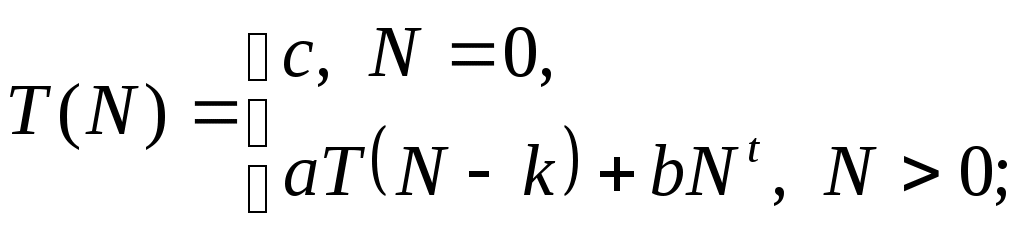
где
, 
, 
, , 
- фиксированные константы. Например, такая ситуация возникает при решении графических задач. Для такого соотношения при 
, где 
, справедлива оценка 1
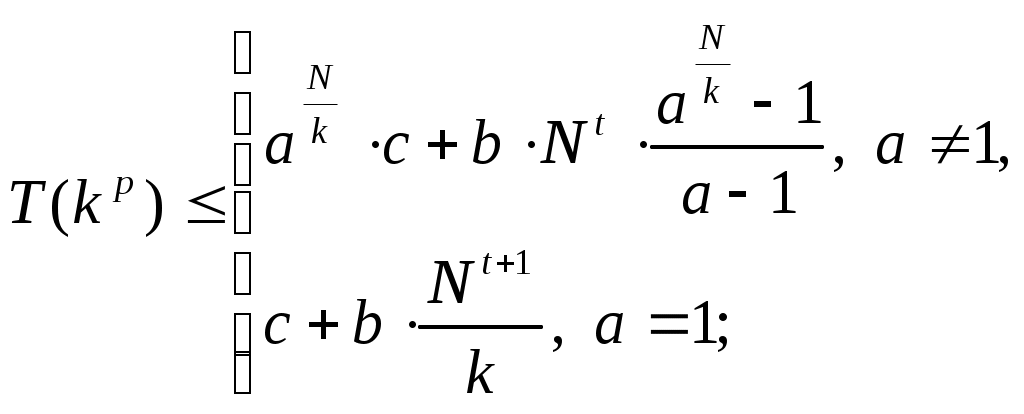
В некоторых случаях для организации рекурсии используется «квадратичное» разбиение, при котором исходная задача размера
разбивается на 
подзадач размера . Для сложности рекурсивного алгоритма возникает следующее рекуррентное уравнение
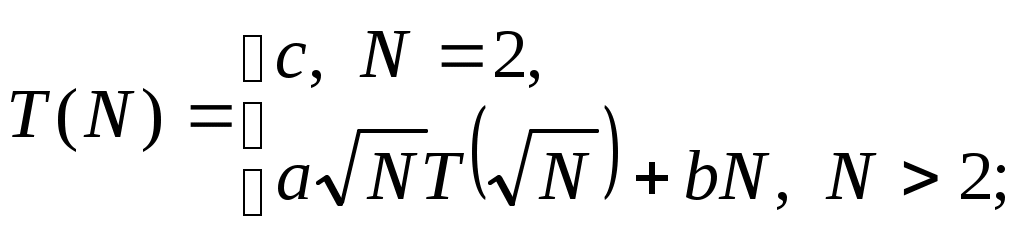
где
, ,
- фиксированные константы. Оно определяет однозначно функцию
при 
таким выражением 2
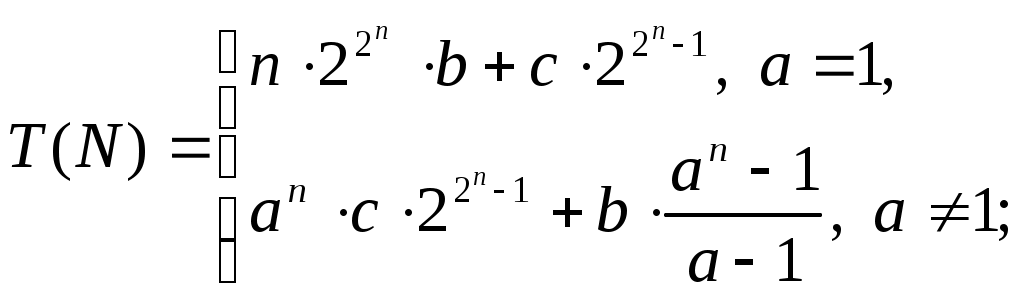
Данные результаты имеют практический интерес. В качестве примера заметим, что для задачи сортировки можно предложить рекурсивные алгоритмы, использующие как разбиение задачи на произвольное фиксированное число подзадач, так и квадратичное разбиение. Эти алгоритмы дают лучшие оценки, чем даже быстрая сортировка бинарным разбиением на подзадачи.
Для задачи умножения матриц использование базового алгоритма умножения
-матриц с умножениями для построения рекурсивного алгоритма, сводящего умножение 
-матриц к умножению 
-матриц приводит к оценкам для сложности :
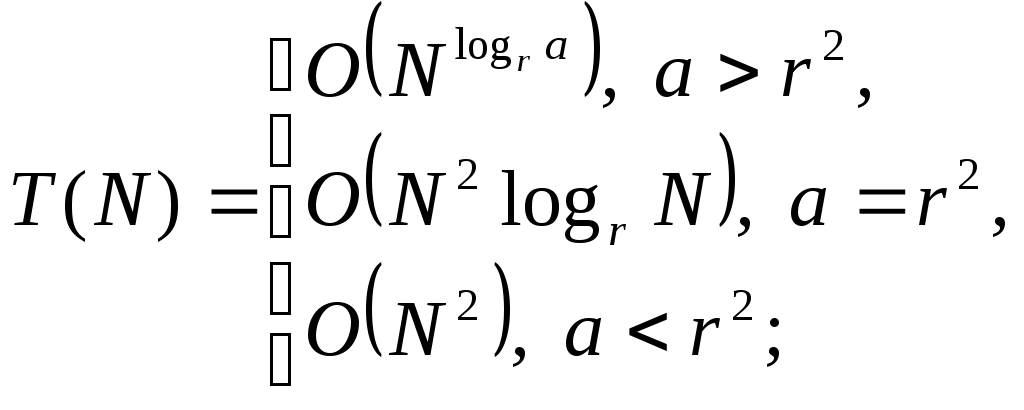
(в алгоритме Штрассена
, 
). В. Пан использовал алгоритм с параметрами 
и 
и получил 
. В настоящее время известны и более лучшие алгоритмы. Усилиями ряда математиков (Пан, Виноград, Романи, Шейхаге, Штрассен, Копперсмит) экспонента сложности матричного умножения последовательно принимала значения: 
, 
, 
,
, 
, 
. Основная проблема - нахождение доказательства равенства 
еще не решена 1.Рассмотрим еще один пример применения полученных результатов. Вернемся к задаче умножения чисел в двоичной записи. Зафиксируем натуральное число
и рассмотрим два 
-битовых числа 
и 
, где 
,
.Разобьем эти числа на
частей
,
.Здесь каждое
и 
, являются 
-битовыми числами, 
. Рассмотрим многочлены
и образуем произведение
. Ясно, что выполнено 
, 
, 
. Поэтому, знание многочлена 
позволяет вычислить произведение
за число действий пропорциональное . Чтобы найти коэффициенты многочлена 
находим значение в 
точках 
, то есть 
. Разрядность чисел 
(соответственно 
) не превышает 
, где - некоторая константа, зависящая oт 
. Ясно, что если 
- сложность умножения -битовых чисел, то сложность умножения -битовых чисел есть 
для некоторой константы 
.Если
- сложность умножения 
-битовых чисел, то справедливо соотношение 
(
- константа). Отсюда и согласно изложенным ранее результатам, получаем 
. Поскольку имеем 
и, обозначая
можно записать 
. Таким образом, доказано, для любого 
существует алгоритм умножения -битовых чисел, для которого сложность удовлетворяет соотношению .Имеются и более эффективные алгоритмы умножения чисел, но они используют уже не цифровые операции 1.
Обобщая полученные результаты, нужно отметить, что многие распространённые и важные алгоритмические задачи допускают рекурсивные решения. Несмотря на кажущуюся громоздкость (ведь на каждом шаге количество подалгоритмов меньшей размерности увеличивается в несколько раз) анализ с использованием аппарата теории сложности показывает, что они зачастую менее трудоёмки, чем обычные итерационные. Однако само получение сложностных оценок не так просто. В большинстве случаев функция сложности определяется с помощью рекуррентных соотношений, нахождение явного её вида представляет некоторые трудности. Справиться с этой проблемой удаётся при специально подобранных значениях размерности исходной задачи. Другие значения требуют отдельного исследования и обычно позволяют получить только грубые оценки.