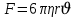Қысым деп бетке түсетiн күштiң осы беттiң ауданына қатынасына тең шаманы айтады. Өлшем бірлігі  Паскаль - 1Па

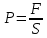(3.1)

Кез келген нүктесiнде жүргiзiлген жанама сол нүктедегi сұйық бөлшегiнiң жылдамдықтарымен сәйкес келетiн сызықтарды ағынсызықтары деп атайды. Ағын сызықтарының жиiлiгi сол жерде сұйықтың жылдамдығын көрсетедi (3.1-сурет). Мысалы, суреттегi А нүктесiндегi сұйықтың жылдамдығы В нүктесiндегi сұйықтың жылдамдығынан үлкен болады. Ағын сызықтарымен шектелген сұйық бөлiгiн ағын сорғысы деп атайды. Кез келген нүктесiндегi сұйықтың жылдамдығының шамасы мен бағыты 

өзгермейтiн ағысты стационар ағыс деп атайды.

Ағыс сипатына байланысты екіге бөлiнедi: егер сұйық қабаттары бiр-бiрiмен араласпай, бiр-бiрiне параллель  қозғалатын болса, мұндай ағыс – ламинар (қабатты) ағыс деп аталады.



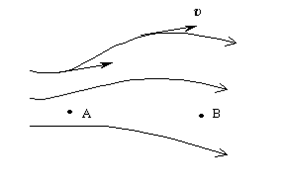
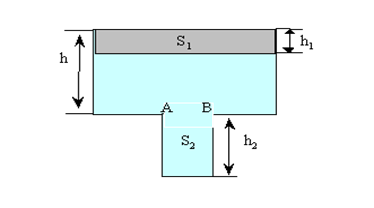
3.1 – сурет 3.2 – сурет
Егер сұйық қабаттары бiр-бiрiмен араласып иiрiлiп қозғалатын  болса, 

мұндай ағыс турбуленттi (иiрiмдi)деп аталады.

---

Ағынның үздіксіздік теңдеуі. 3.2-суреттегiдей түрде жалғастырылған екi ыдыс алайық. Жоғарғы ыдыстағы сұйық h биiктiкке дейiн толтырылған делiк. Ендi екi ыдысты қосатын AB шүмегiн ашсақ, онда сұйықтың бiразы жоғарғы ыдыстан төменгi ыдысқа ағып өтедi. Айталық,  t - уақыт iшiнде жоғарғы ыдыстағы сұйықтың деңгейi h₁ - ге төмендеп, төменгi ыдыс толсын.

Сұйық сығылмайды және үзiлмейдi деп есептесек, онда жоғарғы ыдыстан ағып кеткен сұйық көлемi мен төменгi ыдысқа құйылған сұйық көлемi тең болады: 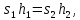(3.2)

мұндағы: s₂- жоғарғы ыдыстың көлденең қимасы,   s₁- төменгi ыдыстың көлденең қимасы, бұл формуланың екi жағын  t - ға бөлсек:    

   немесе      ,

Мұндағы  υ₁- жоғарғы ыдыстағы сұйық ағысының жылдамдығы, 

υ₂- төменгi ыдыстағы сұйық ағысының жылдамдығы. Сонда:

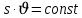(3.3)

Осы өрнектi ағынның үздiксiздiк теңдеуi деп атайды. Ыдыстың  көлденең қимасының сұйық ағысының жылдамдығына көбейтiндiсi тұрақты шама болады.Сұйық ағысының жылдамдығы ыдыстың көлденең қимасына керi пропорционал.

  Бернулли теңдеуi. Идеал сұйықтың қозғалысын (ағысын) сипаттайтын өрнектi 1738 жылы Д.Бернулли (1700-1782) тұжырымдады. Бернулли энергияның сақталу заңын пайдалана отырып, сұйық қысымының жылдамдыққа тәуелдiлiгiн анықтады.   Бұл формуланы қорытып шығару үшiн көлденең қимасы әр түрлi түтiкшедегi идеал сұйықтың қозғалысын қарастырайық (3.3-сурет).

1 және 2 қималардың арасындағы сұйық массасының қозғалуын бақылайық. 

1-ден кейiн, 2 қиманың алдында ағын болмаса да екi қима арасындағы сұйық массасы өз салмағы әсерiнен қозғала бастайды. Алайда, екi қима арасындағы сұйық өз массасы мен  ғана  қозғалып  қоймай,  ол   p₁-p₂ айырмасының әсерiнен  де қозғалысқа  келетiнiн айта кеткен жөн. Сонымен сыртқы күш 

A=A₁+A₂  жұмыс iстейдi, мұндағы A₁- 1қимада iстелетiн жұмыс. 

 



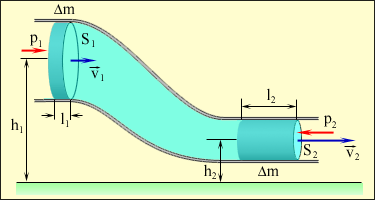
3.3– сурет
A₂- 2қимада iстелетiн жұмыс A₂<0.Энергияның сақталу заңы бойынша 

қималар энергияларының айырымы сұйықты қозғалысқа келтiру үшiн 

iстелетiн жұмыстардың айырымына тең болады:

W₂–W₁=Aнемесе W₂–W₁= A₁–A₂

Мұндағы: W₁, W₂

---

- 1 мен 2  қималардағы сұйықтардың толық энергиялары.

          Толық энергия кинетикалық және потенциалдық энергиялардың қосындысына тең: ,

,

.

W₁,  W₂және A-ның мәндерiн алғашқы формулаға апарып қойсақ, табатынымыз

.

 Ағыстың үздiксiздiк теңдеуiнен    екенiн бiлемiз, олай болса:

.

Екiншi жағынан,   сонда, ,

бұл өрнектiң екi жағын да көлемге (V) бөлсек:

.

Ал 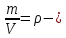     сұйықтың тығыздығы екенiн ескерсек: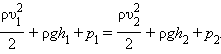



Жалпы түрде алғанда 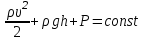(3.4)

Бұл теңдеу Бернулли теңдеуi деп аталады.мұндағы: 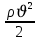  - динамикалық қысым,  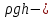-гидравликалық қысым, р  -  статикалық қысым.

Статикалық қысым (р) сұйықтың қозғалысына тәуелсiз, ал динамикалық қысым сұйық қозғалысына тәуелдi болады. Ол сұйық тежелгенде айқын бiлiнедi. Гидравликалық қысым салмақсыздық кезiнде жойылады да, асқын салмақ кезiнде өсе түседi.

Горизанталь құбыр үшiн Бернулли теңдеуi:

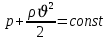
Сұйықтың жылдамдығы артқанда қысымы кемидi.

Нақты сұйықтарда болатын ламинарлық ағыстың жылдамдығы белгілі бір шамаға жеткенде сұйық турбулентті ағысқа ауысады. Осы жылдамдық крезистік жылдамдық деп аталады. Осы крезистік жылдамдық Рейнольде санымен және мына формуламен анықталады. ,

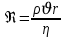Мұндағы 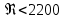болса, онда сұйықта ламинарлық ағыс, 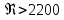болса, онда турбулентті ағыс пайда болады. Сонда алдыңғы формула келесі түрге ауысады:

---

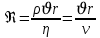, мұндағы 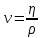– кинематикалық тұтқырлық деп аталады.

Тұтқырлық (ішкі үйкеліс) деп аққыш денелердің (сұйық пен газдың) бір қабатынан екінші қабатына дененің орын ауыстыруына кедергі жасайтын қасиетін айтамыз.

Сұйықтың жоғарғы және төменгі қабаттарын өзара параллель жазықтық екі пластина деп қарастырайық.

Сұйықты ойша жұқа қабаттарға бөлейік. Егер жоғары пластинаны төменгі пластинаға қатысты солдан оңға қарай жылжытсақ, онда оған жабысқан сұйық молекулалары пластинамен бірге дәл сондай жылдамдықпен қозғалады. Бұл молекулалар келесі қабаттың молекулаларын ілестіреді де, процесс осылайша одан әрі жалғаса береді. Төменгі пластинаға жанасып жатқан молекулалар қабаты тыныштықта болады да, басқа қабаттар бірінің бетімен бірі сырғи отырып орын ауыстырады. Төменгі қабаттар алыстаған сайын молекулалар қабатының жылдамдығы арта түседі. Сұйықтың тұтқырлығы жанасқан қабаттардың бір – біріне қарағанда ығысуы кедергі жасайтын күштің пайда болу нәтижесінде байқалады. Бұл күштің табиғатын былай түсіндіруге болады: әр түрлі жылдамдықпен қозғалатын сұйық қабаттары бір – бірімен молекулалар алмасады. Сонда жылдам қозғалатын қабаттағы молекулалар біраз қозғалыс мөлшерін баяу қозғалатын қабатқа береді. Ал баяу қозғалатын қабаттан шапшаң қозғалатын молекулалар жылдамдығы тежеліңкірейді. Сөйтіп, ішкі үйкеліс күші сұйық қабаттарының қозғалу жылдамдықтарын теңестіруге тырысады. Сұйықтың тұтқырлығынан пайда болған кедергінің шамасы сұйық қабаттары жылдамдықтарының айырымына және олардың ара – қашықтығына байланысты болады. Бір қабаттан екінші қабатқа өткен сұйық жылдамдығының өзгерісі артқан сайын ішкі үйкелістің шамасы да артады. Сұйықтың көршілес екі қабаты жылдамдықтары айырымының сол қабаттардың жылдамдық бағытына түсірілген нормаль бойымен есептелінген ара қашықтығына ∆у қатынасының шегі 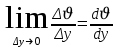(3.5.) жылдамдық градиенті деп аталады.

Ламинарлық ағыс /құйынсыз ағыс / кезінде сұйықтың екі қабатының арасында әсер ететін ішкі үйкеліс күші олардың жанасу бетінің ауданы мен жылдамдық градиетіне тура пропорционал болады:

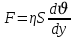/Ньютон формуласы/ (3.6)

Мұндағы: сұйықтың табиғатына және оның күйіне /мысалы температурасына/ байланысты болатын шама η – ішкі үйкеліс коэффиценті немесе динамикалық тұтқырлық коэффиценті, болмаса жай ғана (сұйықтың, газдың) тұтқырлығы деп аталады.

---

Егер (3.6) формуласынан 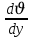және S=1 деп алсақ, онда η=F . (3.7)

Яғни тұтқырлық сан жағынан, бір – бірімен салыстырғанда жылдамдық градиенті бірге тең қозғалыстағы екі қабаттың жанасу бетінің әрбір бірлік ауданында пайда болатын ішкі кедергі күшіне тең. СИ жүйесінде тұтқырлық бірлігі үшін модулі 1 м/с жылдамдық градиенті 1 м жанасу бетіне 1 Н ішкі үйкеліс күшін туғызатын тұтқырлық алынады. Бұл бірлік Паскаль – секунд (Па·с деп белгіленеді) деп аталады. Тұтқырлық коэфициенті температураға тәуелді. Әр сұйық пен газ үшін бұл тәуелділіктің елеулі айырмашылығы бар. Сұйық температурасы жоғарылаған сайын оның тұтқырлығы күрт азаяды. Газда, керісінше температура жоғарылаған сайын тұтқырлық коэффициенті артады. η коэффициентінің температураға байланысты былай өзгеруін сұйық пен газдың ішкі үйкеліс механизмінің әр түрлі болуынан деп түсіну керек.

Жүректің қуаты және механикалық жұмысы. Жүрек – қан айналуының орталық органы және энергия көзі. Ол кеуде қуысында ассиметриялық түрде орналасқан. Жүрек АТФ молекулаларында жинақталған химиялық энергияны механикалық энергияға айналдырып отырады. Импульстік режимде жұмыс жасайтын жүрек – хемоэлектрмеханикалық насос.

1628 жылы ағылшын дәрігері В.Гарней ұсынған тамырлар жүйесі бойынша жүрек қанды тамырлармен айдайтын насос болып саналған. Оның есептеуі бойынша бірнеше сағат ішінде жүректен артерияларға ағатын қанның массасы, адамның өз массасынан әлдеқайда артық.

Жүректің істейтін жұмысы, күштерге өарсы жұмысқа және қанға кинетикалық энергия беруге жүмсалады. Сол жүректің бір рет жиырылғанда істейтін жұмысы А=1Дж. Орта есеппен алғанда жүрек секундына бір рет жиырылады деп санап, оның бір тәулікте атқаратын жұмысын табамыз:

А = 86400 Дж.

Бұлшық еттердің белсенді қозғалысы кезінде бұл жұмыс бірнеше рет артық болуы мүмкін. Егер секундына ұзақтығы t = 0,3с екенін есептесек, онда бір жиырылғандағы жүректің орташа қуаты:

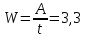Bm

Дене сұйық ішінде қозғалғанда туындайтын құбылысты қарастырайық. Дене тұтқыр ортада қозғалғанда кедергі күш пайда болады. Егер сұйық ішінде шар тәрізді қатты дене қозғалады десек, онда Стокс шарға әсер ететін тұтқырлық күшін шығарып алды:

---

Смотрите также файлы

• Результат попытки теста #.docx

• Сальбутамол 2 10 минута дейін созылатын тс артындаы ысып, басылатын ауырсынулар, белгілері болып табылады.docx

• Отчет о лабораторной работе 1 по общей теории связи измерение параметров детерминированных сигналов.docx

• Уголовная ответственность за экологические преступления.docx

• Отчет о лабораторной работе 2 по общей теории связи дискретизация и восстановление непрерывного сигнала.docx