Файл: Дрістер жинаЫ 1 дріс Таырыбы кіріспе. Материалды нкте механикасы. аралатын мселелер.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 265
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(3.8)
Яғни тұтқырлық күші шардың жылдамдығына, оның радиусына және тұтқырлық коэффициентіне тура пропорционал болады. Шарға әсер ететін күштер бірін-бірі теңгерген кезде, ол тұрақты жылдамдықпен қозғала бастайды. Сонда (6.6) теңдікке сәйкес мына теңдік табылады.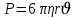
Сұйық ішіндегі шарға әсер ететін Р күші Архимед заңы бойынша P0 – P1 айырымына тең, мұндағы P0 – шардың салмағы, P1 - шармен көлемдес сұйықтың салмағы, сонда: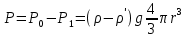
(3.9)
(6.6) және (6.7) теңдеулерін теңестірсек, онда
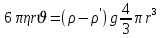
Осы теңдеуден тұтқырлық коэффициентін тапсақ:
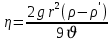(3.10)
Осы формуладан тұтқырлық коэффициентін табуға болады, ол коллойдтық химияда, биологияда, ветеринарияда, медицинада кеңінен қолданылады.
Сұйықтың табиғатына, құрамына байланысты сұйық беті ойыс не дөңес болуы мүмкін. Осы ойыс немесе дөңес бетте беттік керілу күші нәтижесінде қосымша қысым пайда болады. Молекулалар арасындағы молекулалық қысым сұйыққа батырылған денеге берілмейді. Сұйық бетінде орналасқан молекулаға төменгі жағындағы, оң және сол жағындағы орналасқан молекулалар тарапынан күштер ісер етеді де, осы күштер бірін бірі теңестіреді. Ол күштердің қосындысы сұйықтың беттік керілуі деп аталады. ол беттік керілу коэффициентімен сипатталады. Дөңес беттің астында пайда болған қысым төмен бағытталса, ойыс беттің астындағы қосымша қысым жоғары бағытталады. Осы қосымша қысымды анықтайтын Лаплас формуласын жазайық:
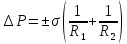(3.11)
∆P – қосымша қысым, σ – беттік керілу коэффициенті, R1 және R2 – түтіктің қисықтық радиустары. Егер бет сфералық болса, R1= R2= Rболады да, Лаплас формуласы келесі түрде жазылады:
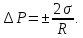(3.12)
Қайталау сұрақтары
№4 дәріс
Тақырыбы: Механикалық тербелістер мен толқындар.
Қаралатын мәселелер: Еркін механикалық тербелістер. Гармоникалық тербелістер. Тербелмелі қозғалыстың энергиясы. Гармоникалық тербелістерді қосу. Күрделі тербеліс, оның гармониялық спектрі. Еріксіз тербелістер. Резонанс. Автотербелістер. Толқындар теңдеуі. Толқынның энергия ағыны. Умов векторы. Толқындардың интерференциясы.
Дененің қозғалыс күйінің белгілі бір шамада қайталанып отыруын тербеліс деп атайды. Мұндай қозғалыстар уақыттың белгілі мезетінде ғана өтіп отырады. Қабырға сағаты маятнигінің қозғалысы, белгілі бір уақыт аралығында дүркін-дүркін қайталанып отыратын қозғалыс күйінің тең уақыт аралығында қайталанып отыруын периодты тербелістер деп атайды.
Гармоникалық тербелмелі қозғалыс деп нүкте қозғалысының тепе-теңдік қалпынан ауытқу шамасының синусоида немесе косинусоида бойымен периодты түрде қайталанып отыруын айтамыз.
Егер тербелістегі нүктенің тепе-теңдік қалпынан ауытқу шамасын х арқылы белгілесек, онда осы ауытқудың уақытқа байланысты өзгеруі мына формуламен өрнектеледі: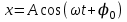
(4.1)
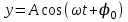
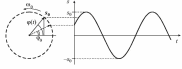
4.1-сурет
Тербелістегі нүктенің тепе-теңдік қалпынан ең үлкен ауытқуын оның амплитудасы (А) деп атайды. Ал тербеліс периодына кері шама тербеліс периодының жиілігі (γ) делінеді. Бұл шама бірлік уақыт ішіндегі тербеліс санын көрсетеді. Егер нүкте шеңберді толық бір айналып шықса, онда φ = 2π, олай болса бұрыштық жылдамдық мына түрде жазылады:
ω = 2π/ T =2πγ
өйткені γ = 1/ T тең. Сонымен (6.1) формуладағы А - тербелістегі нүктенің амплитудасы, ωt + φ0 - оның фазасы. Ал φ0 - тербелістің алғашқы фазасы.
Енді гармоникалық тербелмелі қозғалыс жасайтын нүктенің жылдамдығы мен үдеуін анықтайық. Ол үшін υ = dx/dt және a = dυ/dt ескеріп, (6.1) формуланы жазайық:
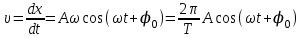; (4.2)
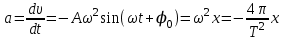; (4.3)
(4.3) формуладағы (-) таңбасы үдеудің ауытқудың бағытына қарама-қарсы екендігін көрсетеді.
Сөйтіп, гармоникалық тербелістегі нүктенің жылдамдығы тепе-теңдік қалыптың маңында, ал үдеуі ауытқудың шеткі мәндерінде максимум мәніне ие болады.
Тербелістегі кез келген материалдық нүктенің кинетикалық энергиясы Ек=mυ2/ 2, осы теңдеуге жылдамдықтың мәнін қойсақ
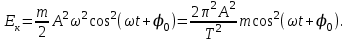
(4.4)
Сонда қозғалыстағы нүктенің ауытқуының шеткі мәндерінің кинетикалық энергиясы нөлге тең, ал тепе-теңдік қалыптың маңында максимум мәніне ие болады.
Тербелістегі дененің жылдамдығы мен үдеуінің мәндері бойынша Ньютон заңын былай жазуға болады: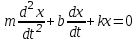
(4.5)
Осы формула өшетін тербелістің дифференциал теңдеуі деп аталады.
Айнымалы қосымша күш арқылы үздіксіз тербелісті еріксіз тербеліс, ал әсер етуші күшті мәжбүр етуші күш деп атайды. Бұл күштің шамасы уақытқа байланысты гармониялық заң бойынша мына түрде жазылады:
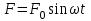(4.6)
F0 – мәжбүр етуші күштің амплитудасы, ω – оның дөңгелектік жиілігі.
Ньютонның екінші заңын еріксіз тербеліс үшін былай жазуға болады:
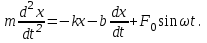(4.7)
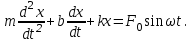(4.8)
Бұл формула еріксіз тербелістің диференциал теңдеуі деп аталады.
Еріксіз тербелістің амплитудасы: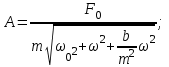
(4.9)
Ал алғащқы фазасы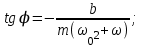
(4.10)
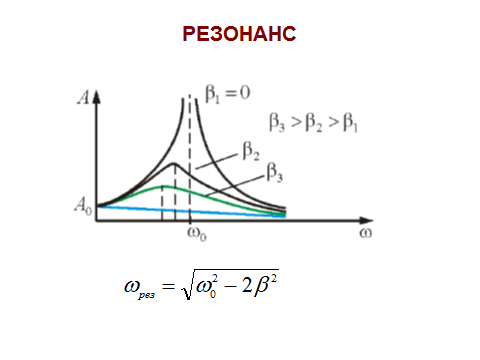
Сөйтіп еріксіз тербеліс кезінде ω = ω0 болады, амплитуданың артуы резонанс құбылысы деп аталады да, оны графикте былай кескіндейді (4.2-сурет).
Гармоникалық осциллятор. Осциллятор деп еркін тербеле алатын түрлі жүйелерді айтады.
а) Механикалық осциллятор ретінде серпімді дененің тербелісін алуға болады.
Дене серпімді тербелу үшін мынадай жүйе құрастырайық: екі ұшы бекітілген серпімді серіппеге т денесін бекітейік (4.1-сурет). Дене ОХ өсі бойымен үйкеліссіз еркін болсын. Бастапқы кезде дене тыныштық күйде болсын, ал оның координаталары x=0, y=0. Денені ОХ өсіненығысқан денеге F= - kx серпімді күші әсер етеді, ал ол әрқашанда О нүктесіне қарай бағытталған. Осы күштің әсерінен дене үдей козғалады. Басқа күштер әсер етпесе, бұл үдеу Ньютонныңекінші заңынан табылады: max = F не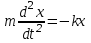
. Демек,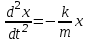
,мұндағы 
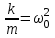деп белгілесек, онда гармоникалық тербелістің теңдеуі шығады: 
.
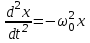Мұның шешуі х = A0 cosω0 t
Сонымен ішкі серпімді күштің әсерінен дене гармоникалық тербеліс жасайды. Тербелістің периоды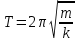
(4.11)
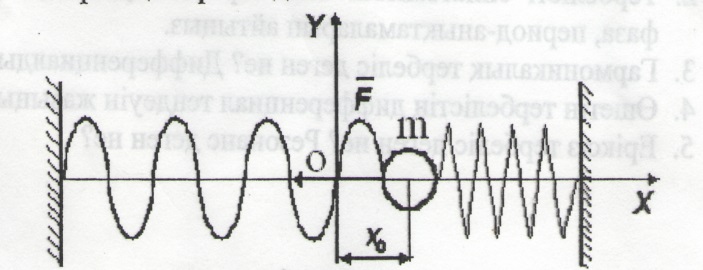
4.2 – сурет 4.3 - сурет
Т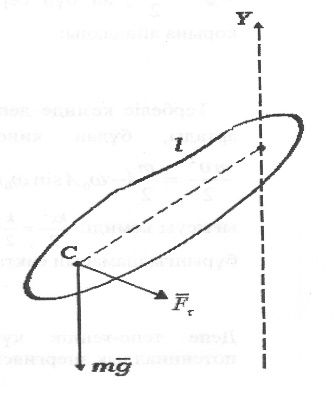
ербелістің периоды массаға жене серпімді серіппенің катаңдығына тәуелді (4.2 – сурет). Сырттан басқа күштер (мысалы, үйкеліс күштері) әсер етпесе, онда дене өшпей тербеледі, демек, жүйеге берілетін энергия сақталады. Жүйеге тән энергия қорын сыртқы күштердің жұмысы арқылы табамыз. Мысалы, серпімді саріппенің х шамасына ығыстыру үшін істелетін жұмыс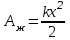
, ал бұл серпімді жүйенің энергиясын арттырады, ол энергия қорына айналады: 
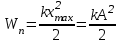. Тербеліс кезінде дене тепе-тендікке қарай үдей қозғалып, жылдамдығы артады, бұдан кинетикалық энергия арта бастайды: ω0A не 
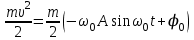, ал потенциалдық энергия азая береді. Бірақ толық энергиябұрынғы шамасын сақтайды: 
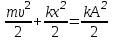. Дене тепе-теңдік күйін ең үлкен жылдамдықпен өтеді, жүйенің потенциалдық энергиясы толығымен кинетикалық энергияға айналады:
, 
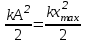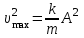
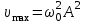(4.12)
Еркін тербелетін серпімді осциллятордың меншікті жиілігін мына қатынастан табамыз: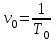
, демек,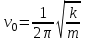
. (4.13)
ә)Физикалық маятник.Механикалық осциллятордың тагы бір түрі-физикалық маятник. Кез келген бір нүктесі арқылы ілініп, тербелетін денені физикалық маятник деп атайды. Ілгешек нүкте дененің ауырлық центріне дәл келмеуі керек. Маятникті тепе-теңдік күйден (ОY осінен) ауытқытсақ оған кері багытталған күш, дәлірек айтсақ күш моменті әсер етеді. Дене ОY өсіне қарай үдей қозғалады. Fτкүші ішкі күш, ол серпімді күшке ұқсайды. Бұл ауытқу бұрышына тәуелді ОY осіне қарай бағытталған. Сондықтан да оны квази серпімді күш деп атайды. Физикалық маятникті қатты дене деп қарастырсақ, онда әсер күші
Fτ=-mgsinα. О нүктесіне қарағанда күш моментін туғызады:
М = IFτ = -Imgsinα.
Осы күш моменті денеге бұрыштың үдеу береді. Айналушы дененің динамикасы бойынша: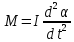
Мұндағы I — маятниктің инерция моменті, ал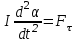
-ға тең, демек, 
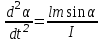. Кіші бұрыштар үшін sinα ≈ α, демек, ал 
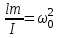деп белгілесек, гармоникалық тербелістің дифференциалдық теңдеуі шығады. Еркін тербелістің өздік жиілігін, периодын былай табамыз
, 
, 
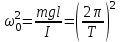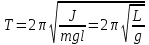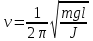(4.14)
Физикалық маятниктің ең қарапайым түрі ұзын жіпке ілінген материалдық нүкте, оны математикалық маятникдеп атайды. Жіп созылмаса, әрі жеңіл болса, шайқалушы дененің инерция моменті оңай табылады, ол I=ml2 , демек,
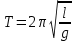. (4.15)
Математикалық маятниктің тербеліс периоды тек ұзындыққа байланысты.Тәжірибе жүзінде Галилей анықтаған болатын.
Яғни тұтқырлық күші шардың жылдамдығына, оның радиусына және тұтқырлық коэффициентіне тура пропорционал болады. Шарға әсер ететін күштер бірін-бірі теңгерген кезде, ол тұрақты жылдамдықпен қозғала бастайды. Сонда (6.6) теңдікке сәйкес мына теңдік табылады.
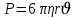
Сұйық ішіндегі шарға әсер ететін Р күші Архимед заңы бойынша P0 – P1 айырымына тең, мұндағы P0 – шардың салмағы, P1 - шармен көлемдес сұйықтың салмағы, сонда:
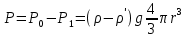(3.9) (6.6) және (6.7) теңдеулерін теңестірсек, онда
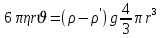
Осы теңдеуден тұтқырлық коэффициентін тапсақ:
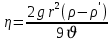(3.10)Осы формуладан тұтқырлық коэффициентін табуға болады, ол коллойдтық химияда, биологияда, ветеринарияда, медицинада кеңінен қолданылады.
Сұйықтың табиғатына, құрамына байланысты сұйық беті ойыс не дөңес болуы мүмкін. Осы ойыс немесе дөңес бетте беттік керілу күші нәтижесінде қосымша қысым пайда болады. Молекулалар арасындағы молекулалық қысым сұйыққа батырылған денеге берілмейді. Сұйық бетінде орналасқан молекулаға төменгі жағындағы, оң және сол жағындағы орналасқан молекулалар тарапынан күштер ісер етеді де, осы күштер бірін бірі теңестіреді. Ол күштердің қосындысы сұйықтың беттік керілуі деп аталады. ол беттік керілу коэффициентімен сипатталады. Дөңес беттің астында пайда болған қысым төмен бағытталса, ойыс беттің астындағы қосымша қысым жоғары бағытталады. Осы қосымша қысымды анықтайтын Лаплас формуласын жазайық:
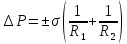(3.11)∆P – қосымша қысым, σ – беттік керілу коэффициенті, R1 және R2 – түтіктің қисықтық радиустары. Егер бет сфералық болса, R1= R2= Rболады да, Лаплас формуласы келесі түрде жазылады:
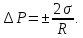(3.12)Қайталау сұрақтары
-
Cұйықтар қозғалысы деген не? Ағынның түрлерін ата. Оларға анықтама бер. -
Сұйықтың ішкі үйкелісі мен тұтқырлығы дегенді түсіндір. -
Стокс ережесін айт. Пуазейль формуласын жаз, ол не үшін керек? -
Ағынның үздіксіздік теңдеуі мен Бернулли заңын жаз. -
Жүректің қуатының жұмысын тұтқырлық арқылы түсіндір. -
Түтікшенің ішіндегі сұйықтың қозғалысын жоғарыдағы заңдарға сүйене отырып түсіндір.
№4 дәріс
Тақырыбы: Механикалық тербелістер мен толқындар.
Қаралатын мәселелер: Еркін механикалық тербелістер. Гармоникалық тербелістер. Тербелмелі қозғалыстың энергиясы. Гармоникалық тербелістерді қосу. Күрделі тербеліс, оның гармониялық спектрі. Еріксіз тербелістер. Резонанс. Автотербелістер. Толқындар теңдеуі. Толқынның энергия ағыны. Умов векторы. Толқындардың интерференциясы.
Дененің қозғалыс күйінің белгілі бір шамада қайталанып отыруын тербеліс деп атайды. Мұндай қозғалыстар уақыттың белгілі мезетінде ғана өтіп отырады. Қабырға сағаты маятнигінің қозғалысы, белгілі бір уақыт аралығында дүркін-дүркін қайталанып отыратын қозғалыс күйінің тең уақыт аралығында қайталанып отыруын периодты тербелістер деп атайды.
Гармоникалық тербелмелі қозғалыс деп нүкте қозғалысының тепе-теңдік қалпынан ауытқу шамасының синусоида немесе косинусоида бойымен периодты түрде қайталанып отыруын айтамыз.
Егер тербелістегі нүктенің тепе-теңдік қалпынан ауытқу шамасын х арқылы белгілесек, онда осы ауытқудың уақытқа байланысты өзгеруі мына формуламен өрнектеледі:
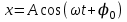(4.1) 4.1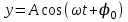-сурет
Тербелістегі нүктенің тепе-теңдік қалпынан ең үлкен ауытқуын оның амплитудасы (А) деп атайды. Ал тербеліс периодына кері шама тербеліс периодының жиілігі (γ) делінеді. Бұл шама бірлік уақыт ішіндегі тербеліс санын көрсетеді. Егер нүкте шеңберді толық бір айналып шықса, онда φ = 2π, олай болса бұрыштық жылдамдық мына түрде жазылады:
ω = 2π/ T =2πγ
өйткені γ = 1/ T тең. Сонымен (6.1) формуладағы А - тербелістегі нүктенің амплитудасы, ωt + φ0 - оның фазасы. Ал φ0 - тербелістің алғашқы фазасы.
Енді гармоникалық тербелмелі қозғалыс жасайтын нүктенің жылдамдығы мен үдеуін анықтайық. Ол үшін υ = dx/dt және a = dυ/dt ескеріп, (6.1) формуланы жазайық:
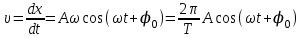; (4.2) 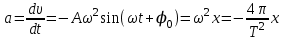; (4.3)(4.3) формуладағы (-) таңбасы үдеудің ауытқудың бағытына қарама-қарсы екендігін көрсетеді.
Сөйтіп, гармоникалық тербелістегі нүктенің жылдамдығы тепе-теңдік қалыптың маңында, ал үдеуі ауытқудың шеткі мәндерінде максимум мәніне ие болады.
Тербелістегі кез келген материалдық нүктенің кинетикалық энергиясы Ек=mυ2/ 2, осы теңдеуге жылдамдықтың мәнін қойсақ
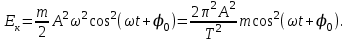
(4.4)Сонда қозғалыстағы нүктенің ауытқуының шеткі мәндерінің кинетикалық энергиясы нөлге тең, ал тепе-теңдік қалыптың маңында максимум мәніне ие болады.
Тербелістегі дененің жылдамдығы мен үдеуінің мәндері бойынша Ньютон заңын былай жазуға болады:
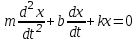(4.5) Осы формула өшетін тербелістің дифференциал теңдеуі деп аталады.
Айнымалы қосымша күш арқылы үздіксіз тербелісті еріксіз тербеліс, ал әсер етуші күшті мәжбүр етуші күш деп атайды. Бұл күштің шамасы уақытқа байланысты гармониялық заң бойынша мына түрде жазылады:
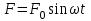(4.6)F0 – мәжбүр етуші күштің амплитудасы, ω – оның дөңгелектік жиілігі.
Ньютонның екінші заңын еріксіз тербеліс үшін былай жазуға болады:
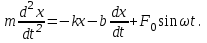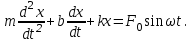(4.7) (4.8)Бұл формула еріксіз тербелістің диференциал теңдеуі деп аталады.
Еріксіз тербелістің амплитудасы:
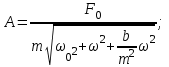(4.9)Ал алғащқы фазасы
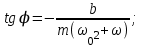(4.10) Сөйтіп еріксіз тербеліс кезінде ω = ω0 болады, амплитуданың артуы резонанс құбылысы деп аталады да, оны графикте былай кескіндейді (4.2-сурет).
Гармоникалық осциллятор. Осциллятор деп еркін тербеле алатын түрлі жүйелерді айтады.
а) Механикалық осциллятор ретінде серпімді дененің тербелісін алуға болады.
Дене серпімді тербелу үшін мынадай жүйе құрастырайық: екі ұшы бекітілген серпімді серіппеге т денесін бекітейік (4.1-сурет). Дене ОХ өсі бойымен үйкеліссіз еркін болсын. Бастапқы кезде дене тыныштық күйде болсын, ал оның координаталары x=0, y=0. Денені ОХ өсіненығысқан денеге F= - kx серпімді күші әсер етеді, ал ол әрқашанда О нүктесіне қарай бағытталған. Осы күштің әсерінен дене үдей козғалады. Басқа күштер әсер етпесе, бұл үдеу Ньютонныңекінші заңынан табылады: max = F не
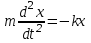
. Демек,
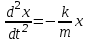,мұндағы 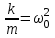деп белгілесек, онда гармоникалық тербелістің теңдеуі шығады: 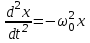.Мұның шешуі х = A0 cosω0 t
Сонымен ішкі серпімді күштің әсерінен дене гармоникалық тербеліс жасайды. Тербелістің периоды
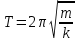(4.11) 4.2 – сурет 4.3 - сурет
Т
ербелістің периоды массаға жене серпімді серіппенің катаңдығына тәуелді (4.2 – сурет). Сырттан басқа күштер (мысалы, үйкеліс күштері) әсер етпесе, онда дене өшпей тербеледі, демек, жүйеге берілетін энергия сақталады. Жүйеге тән энергия қорын сыртқы күштердің жұмысы арқылы табамыз. Мысалы, серпімді саріппенің х шамасына ығыстыру үшін істелетін жұмыс
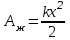, ал бұл серпімді жүйенің энергиясын арттырады, ол энергия қорына айналады: 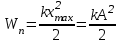. Тербеліс кезінде дене тепе-тендікке қарай үдей қозғалып, жылдамдығы артады, бұдан кинетикалық энергия арта бастайды: ω0A не 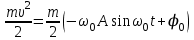, ал потенциалдық энергия азая береді. Бірақ толық энергиябұрынғы шамасын сақтайды: 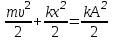. 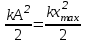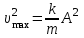Дене тепе-теңдік күйін ең үлкен жылдамдықпен өтеді, жүйенің потенциалдық энергиясы толығымен кинетикалық энергияға айналады: , 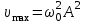(4.12)Еркін тербелетін серпімді осциллятордың меншікті жиілігін мына қатынастан табамыз:
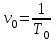
, демек,
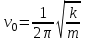. (4.13)ә)Физикалық маятник.Механикалық осциллятордың тагы бір түрі-физикалық маятник. Кез келген бір нүктесі арқылы ілініп, тербелетін денені физикалық маятник деп атайды. Ілгешек нүкте дененің ауырлық центріне дәл келмеуі керек. Маятникті тепе-теңдік күйден (ОY осінен) ауытқытсақ оған кері багытталған күш, дәлірек айтсақ күш моменті әсер етеді. Дене ОY өсіне қарай үдей қозғалады. Fτкүші ішкі күш, ол серпімді күшке ұқсайды. Бұл ауытқу бұрышына тәуелді ОY осіне қарай бағытталған. Сондықтан да оны квази серпімді күш деп атайды. Физикалық маятникті қатты дене деп қарастырсақ, онда әсер күші
Fτ=-mgsinα. О нүктесіне қарағанда күш моментін туғызады:
М = IFτ = -Imgsinα.
Осы күш моменті денеге бұрыштың үдеу береді. Айналушы дененің динамикасы бойынша:
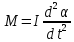
Мұндағы I — маятниктің инерция моменті, ал
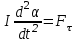-ға тең, демек, 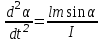. Кіші бұрыштар үшін sinα ≈ α, демек, ал 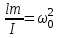деп белгілесек, гармоникалық тербелістің дифференциалдық теңдеуі шығады. Еркін тербелістің өздік жиілігін, периодын былай табамыз 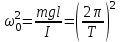, , 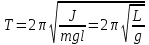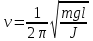(4.14)Физикалық маятниктің ең қарапайым түрі ұзын жіпке ілінген материалдық нүкте, оны математикалық маятникдеп атайды. Жіп созылмаса, әрі жеңіл болса, шайқалушы дененің инерция моменті оңай табылады, ол I=ml2 , демек,
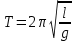. (4.15)Математикалық маятниктің тербеліс периоды тек ұзындыққа байланысты.Тәжірибе жүзінде Галилей анықтаған болатын.