Файл: Организация проблемного обучения математике в начальной школе Содержание.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 46
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
- Ребята, для вас есть задание! Вам нужно понять и дать ответ, в каких текстах присутствует задача, а в каких ее нет.
1. На прошлой неделе мы с вами ходили на прогулку 2 раза. На этой неделе 1 раз.
2. В корзине лежало 7 грибов. Один гриб оказался несъедобным и его выкинули. Сколько грибов осталось в корзине?
3. Мама купила две булочки после работы и принесла домой, а папа купил 3 булочки. Сколько всего булочек окажется вечером дома?
Пояснение:
- Вы должны выбрать те тексты, в которых присутствуют задачи, и объяснить, почему выбрали именно этот текст, а не другой!
- А давайте посмотрим на текст, который не является задачей, можем ли мы из него сформулировать задачу? Попробуйте! [4]
Задание для обучающихся 2 класса
Задача: подвести обучающихся к изучению правила использования скобок в качестве средства обозначения порядка действий.
Обучающиеся производят вычисления с использованием двум разных подходов, которые приводят к одинаковым выражениям, но разным результатам.
1 подход:
Из числа 8 вычесть 3. К полученной разности прибавить 4.
8-3+4=9.
2 подход:
К числу 3 прибавить 4. Из числа 8 вычесть полученную сумму.
8-3+4=1.
– Что вы видите?
Выражения в левой части обоих равенств одинаковые, но их значения разные.
(Появление двух противоречивых фактов – формирование проблемной ситуации «с удивлением»).
– Как вы считаете, почему все-таки получились разные ответы?
– Сравните выражения – чем они похожи? Чем отличаются?
– Какое действие выполняли первым в 1 выражении, какое вторым?
(Дети устанавливают, что разные ответы получились из-за порядка действий.)
Скобки позволяют установить порядок действий, помочь нам произвести вычисления в нужном порядке.
Задание для обучающихся 3 класса
На уроке «Деление с 0 и 1»:
Вставьте пропущенные знаки:
68…1=68 0…38=0 46…0=46 1…21=21 24…1=24 15…0=0
Какие знаки действий мы знаем? (сложение, вычитание, умножение, деление).
Какие знаки поставим в 1 примере? (умножение). Во 2 примере? (умножение). Можем ли мы поставить другой знак, например, деление? (испытывают затруднение, так деление на 1 и 0 еще не решали). Кто может сформулировать тему урока? (Деление на 0 и 1).
7:7=
Необходимо найти такое число, при умножении которого на 7 получится 7. Это число 1. Значит, 7:7=1
5:1=
Найти число, при умножении которого на 1 получается 5. Это число 5, значит, 5:1=5
0:6=
Надо найти число, при умножении которого на 6 получается 0. Это число 0, значит, 0:6=0
В разделе «решение задач» можно использовать проблемные задачи: с недостающими данными; без сформулированного вопроса; с лишними данными; задачи с несколькими решениями; нестандартные задачи.
А сейчас посмотрите на этот рисунок (Рис. 1) лежащий перед вами и выполните задание, которое там описано. Если возникают затруднения, мы их разберем.
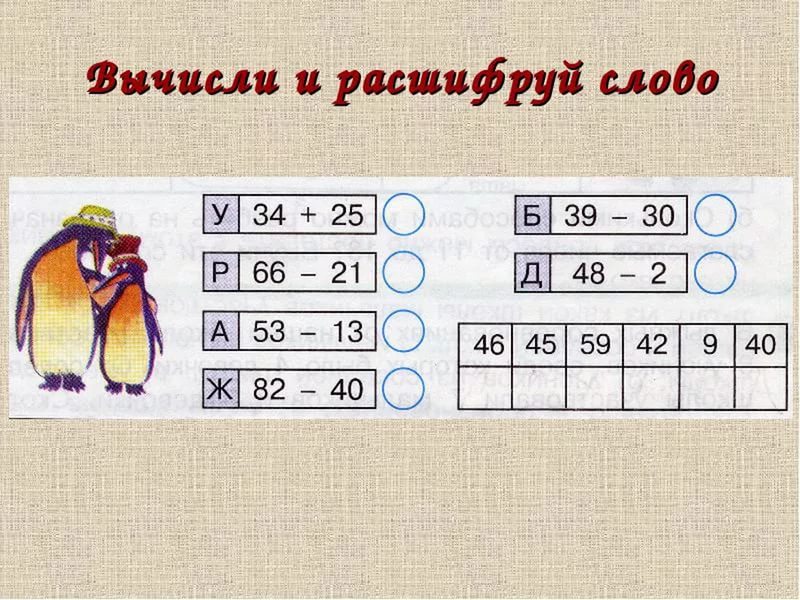
Рис. 1 – Пример занимательного задания
Задание для обучающихся 4 класса
«Открываем формулу площади прямоугольника»
Учитель: Сегодня на уроке я предлагаю вам почувствовать себя в роли дизайнеров. Я держу в руках листы бумаги. Как вы считаете, могут ли они нам сегодня пригодится? Для чего:
Мы будем разрабатывать проект комнаты нашей мечты. Подумайте, как вам удобнее работать: в паре, в группе или индивидуально? (Ребята делятся на группы и рисуют проект детской комнаты, расставляют мебель, картины, спортивные уголки).
После того как все создали проект комнаты, я предлагаю разделить его на квадратные сантиметры.
- Что мы можем для этого использовать? (палетку).
С помощью палетки, мы посчитываем сколько квадратных сантиметров поместилось в этот прямоугольник. Хорошо. Вы справились, подсчитали, что здесь поместилось 200 квадратов, то есть можно сказать, что площадь нашей комнаты в проекте 200 квадратных сантиметров. А если мы вернёмся к нашей любимой передаче. То вспомним, что после того как создали проект, что делали дальше? Правильно воплощали всё это в жизнь, уже в реальность. Так как же дизайнерам не допустить ошибку в расчётах по измерению площади уже настоящей комнаты, чтобы поместилась вся та мебель, которую вы нарисовали, красиво расставили? Или может быть кто-то из вас видел огромную палетку, которую можно было сверху на пол положить. Я, например, не видела. А вы? Как вы думаете, всегда ли с помощью палетки можно измерить площадь? Если нет, то что делать? Палетки нет, но есть длина и ширина комнаты, которые нам известны. Не известны? Тогда мы должны узнать, давайте сначала измерим длину и ширину у нашего проекта детской комнаты. Длина 20 см, ширина 10 см. Что вы заметили необычного? Квадратиков 200, т.е. площадь нашей комнаты 200 квадратных сантиметров. Узнали длину и ширину это 20см и 10 см. Какой вывод можно сделать? Как можно найти площадь прямоугольника? Правильно для того, чтобы получить 200 мы должны 20 умножить на 10. Так чтобы найти площадь прямоугольной комнаты, мы должны что сделать? Правильно, измерить его длину и ширину (в одинаковых единицах) и найти произведение полученных чисел. Существует формула вычисления площади прямоугольника, которую вы уже сами и открыли для себя S = a.b, где, а – длина прямоугольник, b – ширина. Так как же теперь без палетки, мы, будучи дизайнерами, точно узнаем площадь комнаты, длина которой 10 м, а ширина 5 м? Правильно, мы 10м умножим на 5м и получим 50 квадратных метров. Уже будем использовать формулу.
2.2 Рекомендации по использованию проблемного обучения математике в начальной школе
Рассмотрим основные правила и рекомендации по использованию проблемного обучения математике в начальной школе.
Основной принцип реализации проблемного обучения заключается в том, что учитель должен осознанно и, с использованием заранее подготовленного сценария, вступать в творческое взаимодействие с обучающимися. Это предполагает совместные обсуждения вариантов решения задач, подходов к решению и даже спор относительно того, что является верным, а что нет. Так дети приучаются к активной жизненной позиции, избавляются от страхов и комплексов, учатся не боятся высказывать свое мнение, и при этом эффективно реализуется процесс обучения младших школьников математике. Учитель должен выстраивать в такой форме обучения равноправные отношения с обучающимися – это залог корректного использования метода проблемного обучения.
Успеха в проблемном обучении младших школьников помогут достичь следующие рекомендации:
- особой популярностью в процессе обучения пользуются проблемные ситуации, когда учитель намеренно допускает ошибку в примере вычисления.
-в качестве проблемной ситуации могут также выступать занимательные задания.
- эффективны также проблемные ситуации, создающиеся с опорой на жизненные обстоятельства и реалии обучающихся.
- в целях развития дополнительных качеств у обучающихся, которые требуются в обучении, можно использовать задачи на внимание и сравнение.
- для развития мышления и логики можно использовать проблемные ситуации, в которых приводится несколько способов решения заданий. Возможно, что все они верны, а задача обучающихся это понять.
- сформировать задания в форме исследования – еще один способ эффективного проблемного обучения, когда ребята должны на своем опыте что-то узнать, исследовать, добыть знание или получить результат [10].
На этапе подготовки проблемных ситуаций и заданий учителю важно придерживаться следующих условий:
- целенаправленность – верное соотношение цели урока, содержания задачи и подходов к ее реализации;
- бинарность;
-творческая активность;
-учет уже имеющегося опыта работы с использованием проблемного обучения;
-систематичность и последовательность – нельзя перегружать занятие проблемными ситуациям в упражнениях, а также необходимо постепенно усложнять задания в соответствии с приобретением обучающимися нового опыта, навыков и знаний.
- также важна научность содержания задачи;
-должно реализовываться объединение условий эмоциональной, интеллектуальной, волевой и практической деятельности обучающихся.
-единство педагогико-психологических закономерностей в обучении математике [14].
Ключевую роль в процессе реализации проблемного обучения на уроках математики в начальной школе имеет этап методической подготовки учителя.
Задачами учителя на этом этапе являются:
1.Подобрать /сформировать/создать проблемные упражнения.
2.Видоизменияя форму выражения или же определенных условий задачи, придать ей проблемный характер.
При этом учитель должен владеть поисковыми методами обучения, знанием фактического материала, способами постановки вопросов, которые будут показывать противоречия перед обучающимися, а также уметь корректно использовать те термины и понятия, которые уже знакомы младшим школьникам. Одним из важнейших условий является следование возрастным особенностям обучающихся, их способностям и склонностям. При этом проблемная ситуация должна быть достаточно трудной, но посильной для обучающихся.
Таким образом, успешное использование технологии проблемного обучения зависит от педагогического мастерства самого учителя, его возможностей, навыков. Зная и используя приеденные рекомендации, постоянно совершенствуя свой опыт, работу с младшими школьниками, можно сделать эффективной и увлекательной.
Выводы по 2 главе:
Использование технологии проблемного обучения на уроках математики – это не только способ эффективного усвоения нового и закрепления изученного материала по темам, но и активный творческий подход в обучении младших школьников, который является не менее занимательным, чем игровые методы при грамотной разработке сценария такого занятия, четко определенных целях и задачах, а также алгоритмах действий в различных возможных ситуациях, которые могут возникнуть по ходу урока. Это также одна из форм рефлексии, поскольку традиционные способы обучения достаточно быстро надоедают детям- они теряют интерес, вовлеченность, поэтому падает их внимание и настроение. А такие формы обучения, как проблемное обучение, способны замотивировать обучающихся на получение новых математических знаний. Особенно важно использовать задания с опорой на реальные события из жизни младших школьников.
Заключение
Проблемное обучение - набирающий популярность тип развивающего обучения. Его сущность заключается в использовании различных проблемных задач с разным уровнем сложности. В ходе решения этих задач обучающиеся получают новые знания, учатся использовать новые способы действий при решении таких задач. Это, в сою очередь, влияет на формирование творческих способностей- продуктивного мышления, воображения, внимательности и сообразительности.
Задача педагога отслеживать развитие интересов и склонностей обучающихся, давать им посильные для понимания и решения проблемы.
Сама сущность проблемного обучения заключена в том, что знания не передаются ученикам в готовом виде, они должны самостоятельно добыть эти знания, размышляя над проблемной ситуацией или задачей. Важное условие успешного проблемного обучения - прикладной характер таких задач, когда используются задания из жизни учеников.
Естественное возникновение проблемной ситуации в учебном процессе на уроках математики способствует появлению диалога, поскольку решение по готовой схеме, по шаблону в таком случае невозможно, ученик вступает в коммуникацию и пытается решить задачу, используя доступные ему средства; в работу включается память, смекалка и т.д. Поиск решения проблемы приведет обучающегося к заключительному этапу по поиску решения, открывающее ему новое знание, которое затем можно сравнить с формулировкой правила в учебнике.
Задачей активизации младших школьников с помощью проблемного обучения является повышение уровня мыслительной деятельности. Важно при этом обучать его не отдельным хаотичным операциям, а комплексу умственных действий, характерных для решения нестереотипных задач, требующего применения творческой мыслительной деятельности.
Приемы и методы проблемного обучения на уроках математики позволяют детям сравнивать, наблюдать, делать выводы. Они понимают теперь, что не на каждый вопрос может быть готовый ответ, ответ может быть неоднозначным, но при этом каждый из них имеет полное право искать и находить свой ответ, отстаивать свое мнение.
Таким образом, проблемное обучение очень важно использовать на уроках с младшими школьниками. При этом необходимо целенаправленно изучать и исследовать учебную группу.
Список литературы
-
Бабанский Ю.К. Проблемное обучение как средство повышения эффективности учения школьников. Ростов-на-Дону, 1970. -
Бантова М. А., Бельтюкова Г. В. Методика обучения математики в начальных классах: Учеб. пособие для студ. средних пед. учеб. заведений. – 3 издание, испр. – М.: Просвещение, 2016. – 335с. -
Джиоева А.Р., Джиоева Г.Х О реализации проблемного обучения в начальной школе. 2017 г. Режим доступа: file:///C:/Users/Алена/Downloads/o-realizatsii-problemnogo-obucheniya-v-nachalnoy-shkole.pdf Дата обращения: 2.03.2023. -
Использование приёмов проблемного обучения на уроках математики в начальной школе. Режим доступа: https://kopilkaurokov.ru/nachalniyeKlassi/prochee/ispolzovanie_priiomov_problemnogo_obucheniia_na_urokakh_matematiki_v_nachalnoi_s Дата обращения: 13.03.2023. -
Истомина Н. Б. Методика обучения математики в начальных классах: Учеб. пособие для студ. сред. и высш. пед. учеб. заведений. – 4 издание, стереотип. – М.: Издательский центр «Академия», 2013. – 288с. -
Кудрявцев Т.В. Проблемное обучение: истоки, сущность, перспективы. -М. Знание, 2019. - 80 с. -
Логвинов И. И. Основы дидактики: учебно-методическое пособие. - М.: МПСИ, 2018. - 144 с. -
Матюшкин А.М. Проблемные ситуации в мышлении и обучении. М.: Педагогика. 1972 г. С. 170—186. Режим доступа: https://psychlib.ru/mgppu/hre/hre-312.htm#$p312 Дата обращения: 2.03.2023. -
Махмутов Мирза Исмаилович Организация проблемного обучения в школе. М.И. Махмутов. - Москва: Просвещение, 1977. - 240 с. -
Меджидова А.А. Технологии применения проблемного подхода в процессе обучения математике в начальных классах. Режим доступа: https://cyberleninka.ru/article/n/tehnologii-primeneniya-problemnogo-podhoda-v-protsesse-obucheniya-matematike-v-nachalnyh-klassah/viewer Дата обращения: 13.03.2023. -
Проблемное обучение в начальной и средней школе. Научно-образовательный журнал для студентов и преподавателей «StudNet» №12/2020 Режим доступа: file:///C:/problemnoe-obuchenie-v-nachalnoy-i-sredney-shkole.pdf Дата обращения: 2.03.2023. -
Селевко Г.К. Проблемное обучение/ Г.К.Селевко//Школьные технологии. -2016. -№2. -с.61-66. -
Ситаров В.А. Проблемное обучение как одно из направлений современных технологий обучения. 2009 г. Режим доступа: file:///C:/Users/Алена/Downloads/problemnoe-obuchenie-kak-odno-iz-napravleniy-sovremennyh-tehnologiy-obucheniya%20(1).pdf Дата обращения: 2.03.2023. -
Щукина Г.И. Активация познавательной деятельности учащихся в учебном процессе. М.: Просвещение, 1979.