Контрольная работа №4

Задача 1

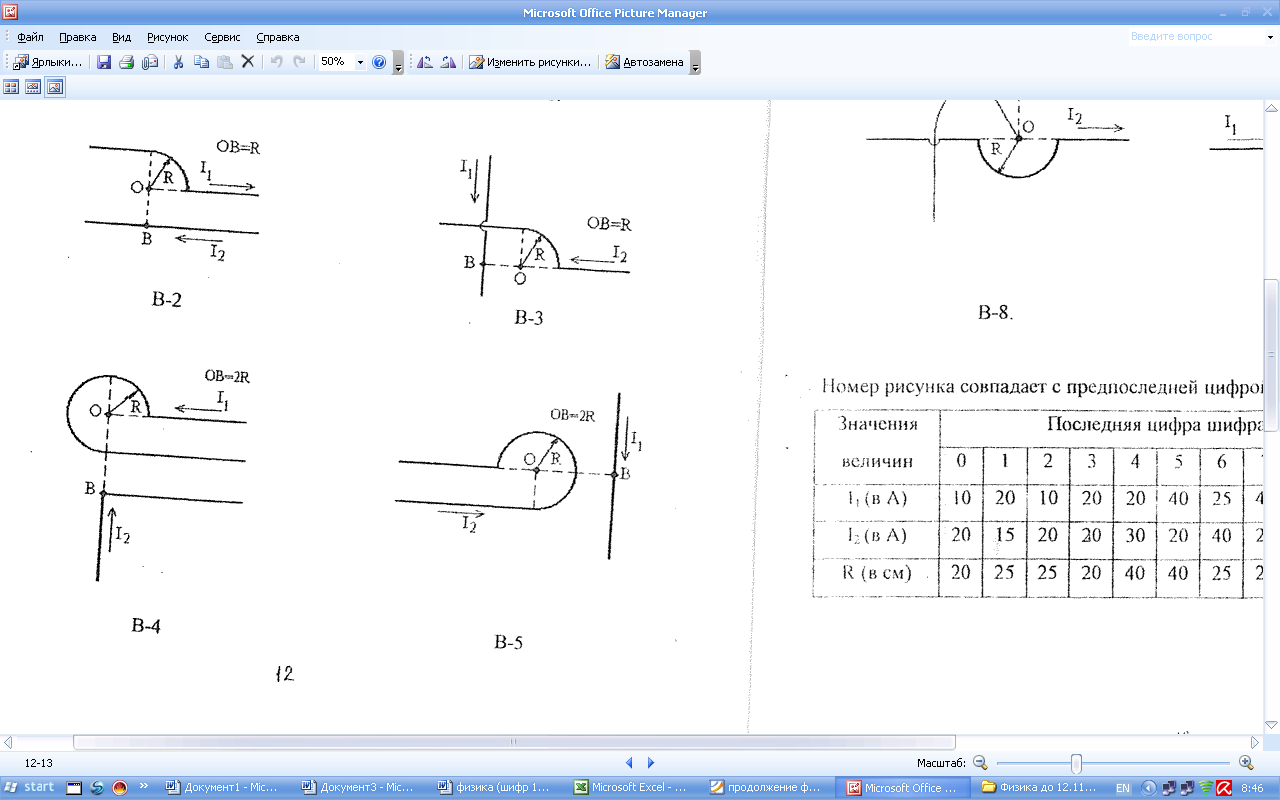
В плоскости расположены два бесконечных контура из тонкого провода. Контурные токи раины А и А. Определить магнитную индукцию В, создаваемую этими токами в точке О.

см

Решение:


3

2

1

4


В соответствии с принципом суперпозиции магнитная индукция поля В=В₁+В₂,

г
1
де В₁ – индукция поля, созданного в точке О током I₁;


3

2
В₂ – индукция поля, созданного в точке О током I₂.

1) найдем индукцию поля, созданного в точке О током I₂;

Разобьем провод на три части: два прямолинейных провода (1 и 3), одним концом уходящие в бесконечность, и дугу полуокружности (2) радиуса R. Тогда магнитная индукция B=B₁+B₂+B₃, где B₁, B₂, B₃ – индукции в точке О, создаваемые током, текущим на первом, втором и третьем участках провода.

Так как точка О лежит на оси провода 1, то В₁=0, поэтому B=B₂+B₃.

Векторы B₂ и B₃ направлены в соответствии с правилом буравчика перпендикулярно плоскости чертежа от нас, следовательно геометрическое суммирование можно заменить алгебраическим: B=B’₂+B’₃.

Магнитная индукция в центре кругового тока В=μ_οI/(2R). Магнитное поле в точке О создается половиной такого тока, поэтому В₂=3μ_οI/(8R).

Магнитную индукцию В₃ найдем, воспользовавшись соотношением: В₂=μ_οI(cosα₁–cosα₂)/(4πr_o).

Так как r_o=R, α₁= – π/2, cosα₁=0, α₂=0, cosα₁=1, то В₃=-μ_οI/(4πR).

Используя найденные выражения для В₂ и В₃, получим:

.

Произведем вычисления: .

2) найдем индукцию поля, созданного в точке О током I₂;

;

3) Векторы В₁ и В₂ взаимно перпендикулярны, но противоположно направлены,поэтому модуль вектора

---

Тл.

Ответ: Тл.


Задача 3

Ион, имеющий массу а.е.м.и заряд q = –е влетает в однородное магнитное поле под углом к вектору мТл. Величина скорости иона км/с. Определить радиус R и шаг h винтовой линии, по которой будет двигаться ион. Найти период обращения Т иона, изобразить примерную траекторию движения иона. Как меняемся со (временем кинетическая энергия Е_кини импульс р иона?

е - заряд электрона, равный Кл.

1а.е.м. – атомная единица массы, равная 1,66 · 10^-27 кг.

Решение:

Ион будет двигаться по винтовой линии, если он влетает в магнитное поле под некоторым углом (α≠π/2) к линиям магнитной индукции. Разложим скорость иона υ на две составляющие: параллельную вектору В (υ₁=υcosα) и перпендикулярную ему (υ₂=υsinα); при этом модуль скорости .

С 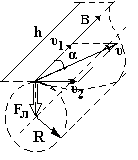корость υ₁ не изменяется и обеспечивает перемещение иона вдоль силовой линии (по вектору В). Скорость υ₂ в результате действия силы Лоренца будет изменяться только по направлению (F_{л ┴} υ₂) Таким образом, ион участвует одновременно в двух движениях: равномерном перемещении со скоростью υ₁и равномерном движении по окружности со скоростью υ₂. При этом период обращения иона T=2πR/υ₂.

Сила Лоренца F_л=QυBsinα=еυ₂Bsinα сообщает электрону нормальное ускорение а_n=υ₂²/R. Согласно второму закону Ньютона F_л = m a_n, откуда

;

---

; ,

поэтому .

Произведем вычисления: .

За время, равное периоду обращения T, ион пройдет расстояние, равное шагу винтовой линии, т.е. h = Tυ₁ , откуда м.

мм.

р=mυ – импульс иона

кг·м/c.

Дж.

Ответ: , мм, кг·м/c, Дж.

Задача 6.

Прямоугольная рамка площадью S = 220 см², содержащая N = 800 витков, вращается с постоянной угловой скоростью рад/с относительно оси, лежащей в плоскости рамки перпендикулярно линиям индукции (в начальный момент времени плоскость рамки также перпендикулярна линиям индукции). Закон изменения индукции от времени Тл. Найти мгновенное значение э.д.с. рамки в момент времени t₁, соответствующий В=0.



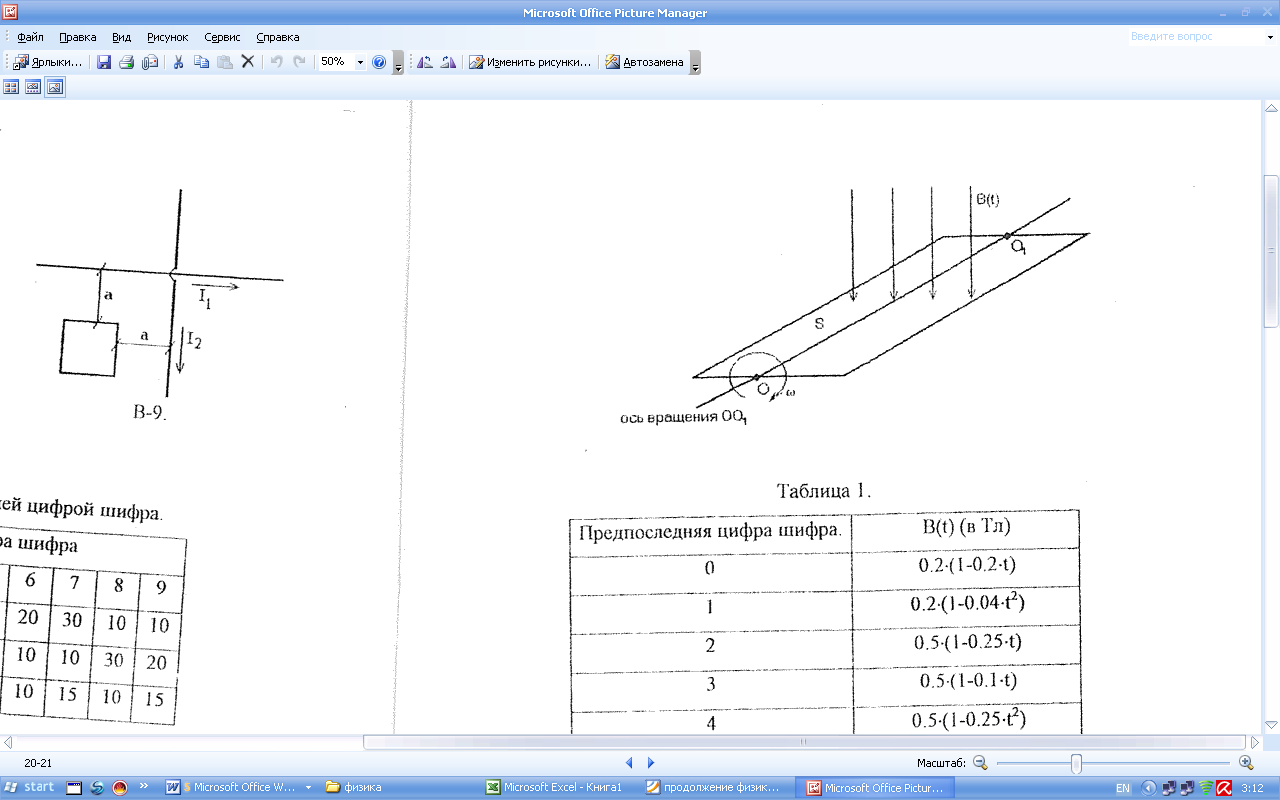
Решение:

Найдем значение времени t₁, соответствующий В=0,





Следовательно, .

В катушке возникает ЭДС индукции

---

Катушка вращается с угловой скоростью вокруг оси, лежащей в плоскости катушки, а В – составляющая магнитной индукции постоянного однородного магнитного поля, перпендикулярная оси вращения катушки. Тогда угол изменяется со временем по закону

. Тогда



.

Произведем вычисления

(В).

Ответ: В.

Задача 4.8

Катушка (без сердечника) длиной  и с площадью поперечного сечения S1 имеет N плотно навитых витков. Катушка соединена параллельно с конденсатором, состоящим из двух пластин площадью S2 каждая, расстояние между пластинами равно d. Диэлектрик – воздух. Максимальное напряжение на пластинах конденсатора равно Umax и соответствует времени t=0.

1)	Определить период колебаний в контуре (сопротивлением контура пренебречь).
2)	На какую длину электромагнитной волны  резонирует контур?
3)	Найти мгновенный ток i(t) в контуре.
4)	Определить максимальное значение объемной плотности энергии Wm магнитного поля катушки.
5)	Зная Wm, найти максимальное значение объемной плотности энергии We электрического поля конденсатора.

Значения	Предпоследняя цифра шифра
величин	0
S1 (в см2)	3
S2 (в см2)	90

Значения	Последняя цифра шифра
величин	6
l (в см)	58
d (в мм)	5.2
N	900
U max(в В)	20

---

Решение:

1) Индуктивность катушки находим по формуле , где - число витков на единицу длины, , тогда

.

Емкость плоского конденсатора , подставим полученные выражение в формулу Томпсона , получим

.

По условию диэлектрик – воздух, то есть , . Получим



с = 565 нс.

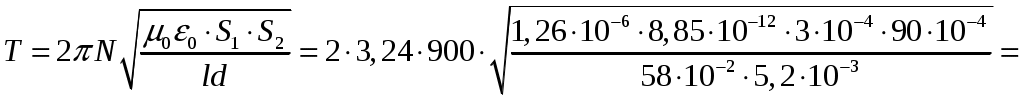
Период колебаний в контуре Т = 565 нс.

2) контур резонирует на длину электромагнитной волны , где с – скорость света.

м.

3) мгновенный ток i(t) в контуре

Пусть начальный момент времени соответствует максимальному заряду q₀ на пластинах конденсатора и закон изменения заряда со временем будет: .

Тогда с учетом соотношения: можно утверждать что при t = 0 напряжение на пластинах также будет иметь максимальное значение. В этом случае уравнение U(t) записывается в виде: , где: ; U_m = 100 В.

Для написания уравнения i(t) учтем, что .

Отсюда получим:

---

Смотрите также файлы

• История развития финансовой системы России.docx

• Отчет по лабораторной работе 1 По дисциплине Компьютерная графика.docx

• Сабаты таырыбы Жеіс мерекесі. Сабаты масаты.docx

• Доклад История вооруженных сил с древности, Великой Отечественной Войны.docx

• Практическая работа 2 Современное учебное занятие в условиях введения обновленных фгос ноо, фгос ооо. Анализ с позиции системнодеятельностного подхода видеофрагментов учебных занятий.docx