Сингулярное разложение широко используется в рекомендательных системах. Оно позволяет найти базисы пространства строк и пространства столбцов, то есть элементарные признаки обоих пространств. Например, если строки матрицы соответствуют читателям, столбцы – книгам, а сама матрица содержит оценки, которые пользователи поставили книгам, то сингулярное разложение матрицы выделит "типичных читателей" и "типичные книги". Каждого реального читателя и каждую реальную книгу можно представить линейной комбинацией "типичных", после чего будет достаточно легко рассчитать ожидаемую оценку любой книги любым читателем.

Методов, позволяющих современным компьютерам обрабатывать огромные разреженные матрицы пользовательских оценок за приемлемое время, очень мало, так что сингулярное разложение матриц применяется очень широко.

Сингулярное разложение матриц (SVD)

Квадратная матрица называется ортогональной, если все ее столбцы ортонормальны – норма каждого из них равна единице, и все они попарно ортогональны, то есть образуют ортонормальный базис. Ортогональные матрицы обладают следующими свойствами:

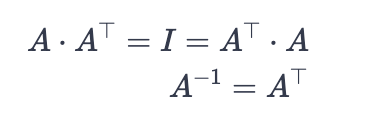
Сингулярное разложение матрицы вводится следующей теоремой линейной алгебры: любую невырожденную прямоугольную матрицу A^m*n можно представить в виде произведения трех матриц U^m*m, E^m*n и V^n*n, где U и V – ортогональные матрицы, а E – прямоугольная матрица, в которой все элементы, кроме диагональных, равны нулю.


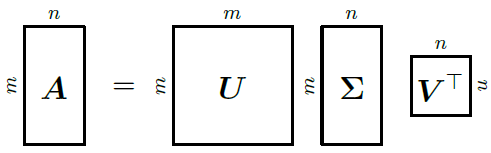
Сингуля́рное разложе́ние — определённого типа разложение прямоугольной матрицы, имеющее широкое применение, в силу своей наглядной геометрической интерпретации, при решении многих прикладных задач. Переформулировка сингулярного разложения, так называемое 

---

разложение Шмидта, имеет приложения в квантовой теории информации, например, в запутанности.

Сингулярное разложение матрицы �  позволяет вычислять сингулярные числа данной матрицы, а также левые и правые сингулярные векторы матрицы � :

• 
  левые сингулярные векторы матрицы �  — это собственные векторы матрицы ��∗ ;
  
• 
  правые сингулярные векторы матрицы �  — это собственные векторы матрицы �∗� .
  

Где �∗ — эрмитово-сопряжённая матрица к матрице � , для вещественной матрицы �∗=�� .

Сингулярные числа матрицы не следует путать с собственными числами той же матрицы.

Сингулярное разложение является удобным при вычислении ранга матрицы, ядра матрицы и псевдообратной матрицы.

Сингулярное разложение также используется для приближения матриц матрицами заданного ранга.

http://www.machinelearning.ru/wiki/index.php?title=Сингулярное_разложение

---

Смотрите также файлы

• 6 сынып аза тілі Т2.docx

• Введение теоретические аспекты развития теневой экономики 6.docx

• Кп тіл білгім келеді.docx

• Вывод Социально коммуникативное развитие.docx

• Пособие по формированию у детей пространственных представлений (комплекс из зрительных диктантов для детей 56 лет).pptx