Добавлен: 07.11.2023
Просмотров: 99
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра «Гидрогазодинамика трубопроводных систем и гидромашины»
Курсовая работа
По дисциплине «Гидравлика и нефтегазовая гидромеханика»
на тему:
«Гидравлический расчет сложного трубопровода»
Работу выполнил:
Студент 2 курса
Горно-нефтяного
Факультета
Группы БГР-21-01
Якупов И.Р.
Научный руководитель:
Сотрудник кафедры ГТ
Старший преподаватель
Нигматуллина Э.А.
Уфа, 2023 г.
Содержание
| Введение | 3 | ||||||||||||
| 1 Теоретическая часть | 4 | ||||||||||||
| 2 Расчётная часть | 7 | ||||||||||||
| 2.1 Задача 1. Гидравлический расчёт сложного трубопровода | 7 | ||||||||||||
| 2.2 Задача 2. Определение расхода при закрытой задвижке 3аключение | 18 20 | ||||||||||||
| Список использованных источников
| 21 |
Введение
Целью курсовой работы является развитие умения самостоятельного решения прикладных задач по гидростатике и гидродинамике в области эксплуатации объектов транспорта и хранения нефти, газа и продуктов переработки. Выполнение курсовой работы закрепляет навыки практического применения таких основных вопросов гидравлики, как:
- основное уравнение гидростатики
;
- силы давления жидкости на плоские и криволинейные поверхности;
- уравнение Бернулли;
- уравнение неразрывности;
- режимы течения жидкости;
- гидравлические сопротивления;
- гидравлический расчет трубопроводов и др.
1 Теоретическая часть
Для решения задач требуется определенная база знаний, то есть умение руководствоваться и опираться на основные законы и формулы. Ниже представлены законы, формулы и упрощения, требуемые для решения задачи.
Уравнение Бернулли для элементарной струйки при установившемся движении: удельная механическая энергия при установившемся движении элементарной струйки идеальной жидкости, представляющая собой сумму удельной потенциальной энергии положения и давления и удельной кинетической энергии, есть величина постоянная:
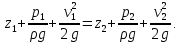
При движении реальной жидкости, обладающей вязкостью, возникают силы трения между ограничивающими поток поверхностями и между слоями внутри самой жидкости. Для преодоления этих сил трения расходуется энергия, которая превращается в теплоту и рассеивается в дальнейшем движущейся жидкостью. Поэтому для практического применения уравнение Бернулли видоизменяется:
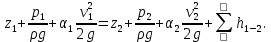
В данном уравнении:
z - геометрический напор;
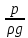 - пьезометрический напор;
- пьезометрический напор; 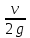 - скоростной напор;
- скоростной напор; 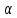 - коэффициент Кориолиса;
- коэффициент Кориолиса; 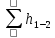 — потери напора.
— потери напора.Потери напора в трубах выражаются формулой Дарси-Вейсбаха:
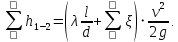
В данном уравнении:
l - длина трубы;
d - диаметр трубы;
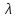 - коэффициент гидравлического сопротивления;
- коэффициент гидравлического сопротивления; 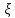 - коэффициент местного сопротивления;
- коэффициент местного сопротивления; 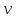 - средняя скорость потока в трубе.
- средняя скорость потока в трубе.
Средняя скорость потока в трубе выражается формулой:
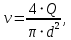
где Q - расход жидкости в трубе.
Коэффициент гидравлического сопротивления
 зависит от режима течения жидкости и является функцией расхода Q и числа Re, где Re — число Рейнольдса, определяемое по формуле:
зависит от режима течения жидкости и является функцией расхода Q и числа Re, где Re — число Рейнольдса, определяемое по формуле: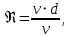
где
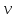 - кинематическая вязкость.
- кинематическая вязкость.Первое и второе критические числа Рейнольдса определяются по формулам:
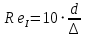 ;
; 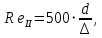
где
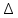 - эквивалентная шероховатость труб, определяемая по справочникам.
- эквивалентная шероховатость труб, определяемая по справочникам.Таблица 1 - Зависимость коэффициента гидравлического сопротивления от режима течения
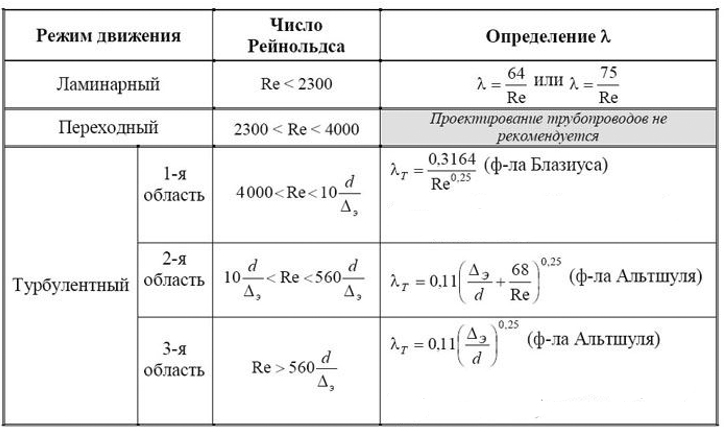
Обычно сложные трубопроводы являются длинными, в уравнениях Бернулли можно пренебрегать скоростными напорами.
Эти допущения упрощают расчеты, поскольку позволяет считать одинаковыми напоры потоков в концевых сечениях труб, примыкающих к данному узлу, и использовать в уравнениях Бернулли понятие напора в данном узле.
2 Расчётная часть
2.1 Задача 1. Гидравлический расчёт сложного трубопровода.
Задача: Резервуары A и B с постоянными и одинаковыми уровнями соединены системой трубопроводов, длины и диаметры. Все трубы расположены в одной горизонтальной плоскости. Определить, при каком избыточном давлении Pмн в резервуаре A расход в трубе 4 будет равен Q. Каков суммарный расход из резервуара A в резервуар B? Исходные данные принять по таблице 2.
Таблица 2 - Исходные данные
| L1, м | L2, м | L3, м | L4, м | d1, м | d2, м | d3, м | d4, м | 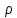 кг/м3 | ʋ∙10-4, м2/с | Q4, л/с |
| 380 | 195 | 80 | 340 | 0,215 | 0,125 | 0,11 | 0,11 | 860 | 0,09 | 1,33 |
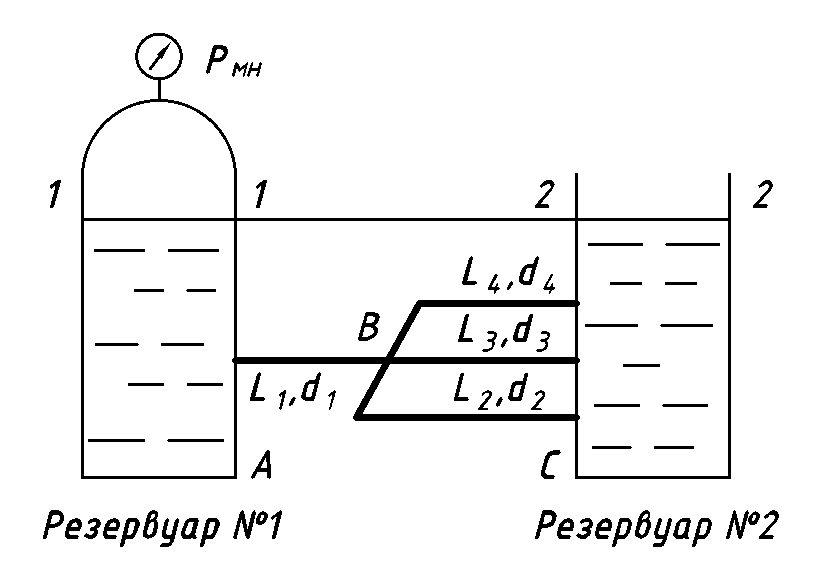
Рисунок 1 – Схема трубопровода к задаче №3
Напишем все возможные выражения определения напора в точке B:
HB=H2+
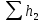 ;
; 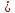 (1)
(1)HB=H2+
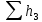 ;
; 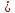 (2)
(2)HB=H2+
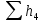 ;
; 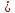 (3)
(3)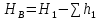 .
. 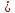 (4)
(4)Из них следует, что
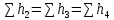 .
. 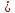 (5)
(5)Для выбранных сечений 1-1 и 2-2 составляем уравнение Бернулли и определяем отдельные его слагаемые.
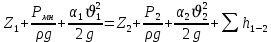 .
. 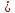 (6)
(6)Где: Z – геометрический напор;
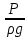 – пьезометрический напор – вертикальное расстояние между центром тяжести сечения и уровнем жидкости в пьезометре; ʋ – средняя скорость потока; α – коэффициент Кориолиса;
– пьезометрический напор – вертикальное расстояние между центром тяжести сечения и уровнем жидкости в пьезометре; ʋ – средняя скорость потока; α – коэффициент Кориолиса; 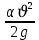 – скорости напора в сечении;
– скорости напора в сечении; 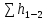 – гидравлические потери напора, которые равны сумме потерь напора по длине трубопровода и потерь напора в местных сопротивлениях.
– гидравлические потери напора, которые равны сумме потерь напора по длине трубопровода и потерь напора в местных сопротивлениях.Упростив данное выражение, получим:
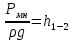 .
. 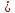 (7)
(7)Потери на участке 1-2 складываем из потерь на участке АВ и ВС:
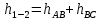 .
. 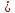 (8)
(8)Найдем потери на участке ВС с помощью формулы Дарси-Вейсбаха;
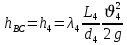
.
 (9)
(9)Где:
 – коэффициент гидравлического трения; L - длина трубопровода; d – диаметр трубопровода;
– коэффициент гидравлического трения; L - длина трубопровода; d – диаметр трубопровода; Найдем среднюю скорость в трубопроводе 4:
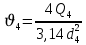 =
= 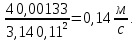
 (9)
(9)Где: Q – расход жидкости в трубопроводе.
Найдем число Ренольдса и коэффициент Дарси в трубопроводе 4:
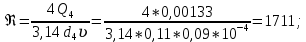
 (10)
(10)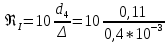 =18333;
=18333;  (11)
(11)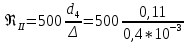 =916650.
=916650.  (12)
(12)Где: ʋ - кинематическая вязкость;
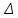 – эквивалентная шероховатость. Для умеренно заржавевших стальных труб: 0,4*10-3 м.
– эквивалентная шероховатость. Для умеренно заржавевших стальных труб: 0,4*10-3 м.Re <2320 – ламинарный режим течения жидкости;
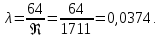 #(13)
#(13)Найдем потери в трубопроводе 4:
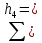
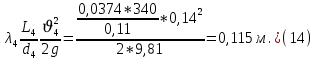
Так как нам неизвестен расход в трубопроводах 3 и 2, но известно, что
 , то необходимо найти расход для каждого из трубопроводов, чтобы вычислить суммарный расход и соответственно расход в трубопроводе 1.
, то необходимо найти расход для каждого из трубопроводов, чтобы вычислить суммарный расход и соответственно расход в трубопроводе 1.Подберём произвольно по 10 значений расхода для 3 и 2 трубопроводов. С помощью формулы Дарси-Вейсбаха найдем для каждого значения среднюю скорость, число Ренольдса, коэффициент гидравлического трения и потери. Затем графоаналитическим методом для каждого из трубопроводов найдем нужный расход, советующий нужной нам потери (0,115 м).
| Q2 (м3/ч) | ʋ2 (м/c) | Re | 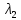 |  (м) (м) |
| 0 | 0 | 0 | 0 | 0 |
| 0,0005 | 0,041 | 566 | 0,1131 | 0,015 |
| 0,001 | 0,081 | 1132 | 0,0565 | 0,030 |
| 0,0015 | 0,122 | 1698 | 0,0377 | 0,045 |
| 0,002 | 0,163 | 2264 | 0,0283 | 0,060 |
| 0,0025 | 0,204 | 2830 | 0,0434 | 0,143 |
| 0,003 | 0,244 | 3395 | 0,0429 | 0,204 |
| 0,0035 | 0,285 | 3961 | 0,0416 | 0,269 |
| 0,004 | 0,326 | 4527 | 0,0404 | 0,341 |
| 0,0045 | 0,367 | 5093 | 0,0395 | 0,422 |
| 0,005 | 0,407 | 5659 | 0,0386 | 0,510 |