Файл: Исследование движения жидкости и газа в пористой среде.docx

Министерство образования и науки Российской Федерации

Филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования

«Уфимский государственный нефтяной технический университет»

в г. Октябрьском

Кафедра разведки и разработки нефтяных и газовых месторождений


Курсовая работа

по курсу «Подземная гидрогазодинамика»

на тему «Исследование движения жидкости и газа в пористой среде»
Выполнил: ст. гр. БГР 12-11 Сабитова А.И.

Октябрьский,2014

Содержание


1. Введение
Природный газ является ценнейшим химическим сырьем, из которого получаются самые разнообразные продукты его переработки, использование его в промышленности, помимо огромной экономии в расходовании твердого и жидкого топлива и резкого сокращения перевозок, приводит к интенсификации производственных процессов и меньшему загрязнению окружающей среды. Поэтому, рациональная эксплуатация газовых залежей, базирующаяся на научных исследованиях, является важнейшей задачей газовой отрасли также, как и установление аналитических основ разработки газовых залежей, которые, в свою очередь, строятся на научных теориях движения газа в пористой среде и скважине.

Остановимся на диагностике газовой скважины по результатам гидродинамических исследований при установившейся фильтрации, что включает в себя и исследования и аналитические основы разработки газовых залежей.

---

2. Цель и задачи курсовой работы

1. 
   углубление и закрепление теоретических знаний, полученных во время лекционных занятий и при самостоятельном изучении курса;
   
2. 
   привитие навыков самостоятельной работы с учебной и научной литературой;
   
3. 
   выработка аналитического мышления при изучении и решении поставленных вопросов и задач;
   
4. 
   выработка умения грамотно и сжато излагать суть вопроса, поставленного в теме курсовой работы;
   
5. 
   привитие навыков выполнения расчетов по тем или иным формулам, применения системы единиц измерения СИ;
   
6. 
   привитие умения делать анализ и вывод по полученным результатам;
   
7. 
   привитие навыков оформления курсовой работы согласно предъявляемым требованиям.
   

3. Анализ работы газовой скважины в прямоугольном секторе, ограниченном сбросами, при установившемся режиме фильтрации газа по закону Дарси

3.1 Метод источников и стоков

Месторождения нефти и газа разрабатываются с использованием различных типов скважин. Количество этих скважин определяется из условий темпа обеспечения заданного отбора из месторождения. При этом необходимо учитывать тот факт, что скважины взаимодействуют. К примеру, увлечении числа эксплуатационных скважин, прирост суммарного дебита замедляется.

Для решения данной курсовой работы рассмотрим наиболее простой случай: пласт считается плоским, а скважины точечными источниками или стоками.

Течение называется потенциальным, если существует такая скалярная функция Ф, что градиент от нее, взятый с обратным знаком, равен вектору скорости, то есть выполняется равенство:
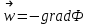(1)


При этом скалярная функция Ф называется потенциалом данного течения.

Если в законе Дарси принять k и μ константами, то получим:
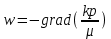(2)

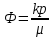(3)

На основании формулы (3) можно сделать вывод о том, что течение жидкостей с постоянной вязкостью в недеформируемых пластах потенциально.

Будем называть точечным стоком, точку, которая поглощает жидкость. По сути это добывающая скважина с бесконечно малым диаметром. На плоскости вокруг точечного стока, линии тока будут представлять собой прямые линии, направленные к скважине, а линиями равного потенциала будут окружности (Рис. 1.а). Источником будем называть нагнетательную скважину, из которой жидкость попадает в пласт. У источника линии тока представляют собой прямые линии, но направленные от скважины (Рис. 1.б).

---

Рис. 1



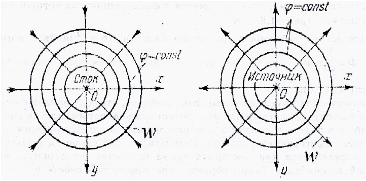
а- сток б-источник


Для нахождения потенциала добывающей скважины (стока) запишем уравнение (2) в цилиндрической системе координат:


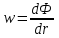
Введем понятие удельного дебита q, приходящегося на единицу мощности пласта:




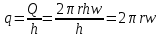
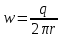
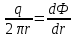(4)


После разделения переменных и интегрирования (4), получим:
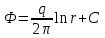(5)

Представим (5) в Декартовой системе координат:
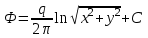(6)


Подставив выражение (6) в уравнение Лапласа, нетрудно убедиться в том, что оно удовлетворяется:


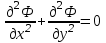
газовая скважина пористая среда

Поскольку уравнение Лапласа линейно и однородно, его решения обладают важным свойством: сумма частных решений уравнения и произведение частного решения на константу, также являются его решением. Это свойство позволяет использовать при решении задач метод суперпозиции. С точки зрения гидромеханики это означает, что если задан потенциал каждой i-ой скважины, когда в пласте работает одна единственная i-ая скважина, то при совместной работе в пласте N скважин решение находится алгебраическим суммированием потенциалов всех действующих скважин. Таким образом, при совместной работе в пласте N скважин результирующий потенциал в произвольной точке М находится как сумма потенциалов всех скважин:
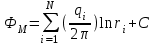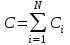, где (8)


где r_i – расстояние от точки М до i-ой скважины; С_i – постоянные интегрирования.

---

Вышеизложенные формулы применимы лишь для несжимаемой жидкости. При фильтрации газа можно использовать метод суперпозиции, но для потенциалов, определенных через функцию Лейбензона. Поэтому нужно ввести потенциал не для вектора скорости фильтрации, а для вектора массовой скорости фильтрации:


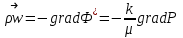
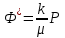(9)







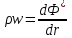
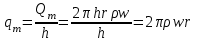
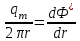
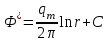(10)


Формула (9) определяет потенциал добывающей газовой скважины (стока). Полученное значение потенциала, как и функция Лейбензона удовлетворяет уравнению Лапласа, следовательно, по аналогии со сжимаемой жидкостью можно записать результирующий потенциал в произвольной точке М при совместной работе N скважин:
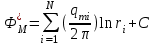, где (11)

3.2 Дебит газовой скважины расположенной в прямоугольном секторе пласта, ограниченном сбросами

Для нахождения дебита скважины, расположенной в прямоугольном секторе (Рис.2), необходимо реальную скважину отразить относительно непроницаемых границ, при этом дебиты отраженных скважин должны иметь тот же знак, что и дебит реальной скважины (Рис.3).

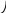
ρ

α


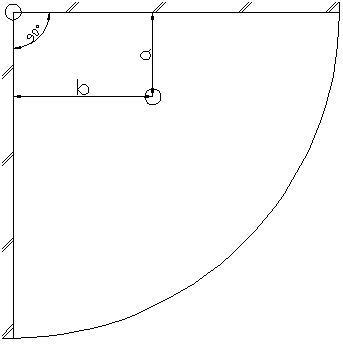
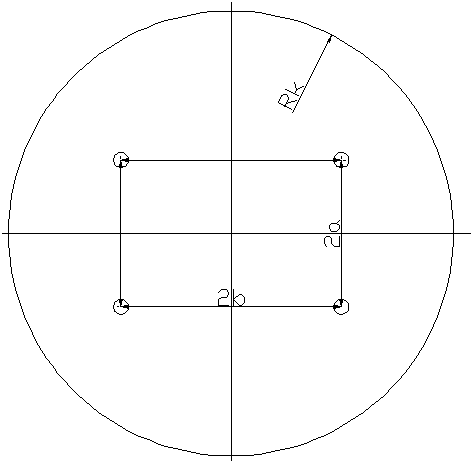
Рис.2 – скважина, расположенная Рис.3 - отражение реальной в прямоугольном секторе скважины относительно непроницаемых границ
Использую формулу (11), определим потенциал в точке М, последовательно располагая ее на забое реальной скважины и на контуре питания.

---

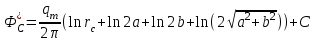(12)

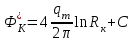, если R_к>>r_c, a, b (13)
Вычтем равенство (13) из (12) и выразим q_m:
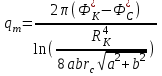(14)

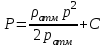(15)
Уравнение (15) выражает функцию Лейбензона для совершенного газа. Запишем выражение для определения массового дебита газовой скважины, расположенной в прямоугольном секторе, ограниченном сбросами на основании формул (9), (14) и (15):
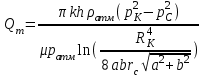(16)
Для удобства проведения расчетов уравнение (16) можно записать в цилиндрических координатах:
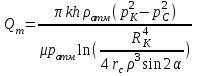(17)

В случае, если добывающая скважина расположена в круговом пласте на расстоянии ρ от его центра до, ее массовый дебит определяется по формуле:
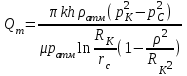(18)

3.3 Распределение давления в прямоугольном секторе

Для того чтобы найти распределение давления вдоль луча, проходящего через вершину сектора и центр скважины, необходимо реальную скважину отразить относительно непроницаемых границ, при этом дебиты отраженных скважин должны иметь тот же знак, что и дебит реальной скважины.

А'

А’’

А

О

М


Рис.4 – прямоугольный сектор пласта
Определим давление в точке М, расположенной на луче, соединяющем вершину сектора и центр скважины, между скважиной и контуром питания (Рис.4). Обозначим через ρ – расстояние от вершины сектора до центра скважины, R – расстояние от вершины сектора до точки М. Определим потенциал в точке М при помощи уравнения (18) и теоремы косинусов:

---