Файл: Исследование движения жидкости и газа в пористой среде.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 63
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2. Цель и задачи курсовой работы
3.2 Дебит газовой скважины расположенной в прямоугольном секторе пласта, ограниченном сбросами
3.3 Распределение давления в прямоугольном секторе
4.1 Исследование зависимости дебита газовой скважины от ее координат внутри сектора
4.2 Распределения давления вдоль луча, проходящего через вершину сектора и центр скважины
Рис.7 – распределение давления при ρ = 1000 и = 30
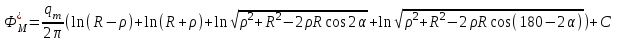
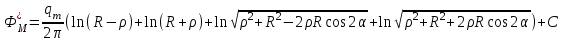
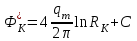
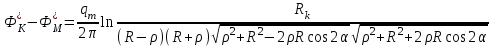
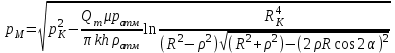
Рассмотрим случай, когда точа М расположена между вершиной сектора и центром скважины. Тогда значение потенциала в точке М будет равно:
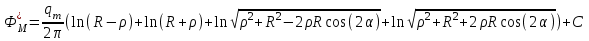
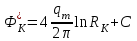
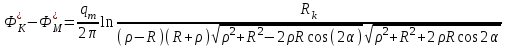
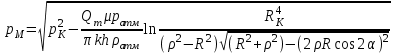
Таким образом, формула распределения давления вдоль луча, проходящего через вершину сектора и центр скважины имеет вид:
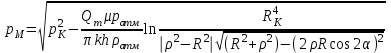 (19)
(19)Если добывающая скважина расположена ацентрично в круговом пласте, на удалении ρ от его центра, то распределение давления по пласту определяется с помощью принципа суперпозиции и задается формулой:
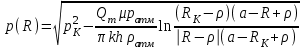 , где
, где 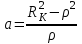 (20)
(20)4. Расчетная часть
4.1 Исследование зависимости дебита газовой скважины от ее координат внутри сектора
-
Исследование зависимости дебита газовой скважины от угла α между непроницаемой границей и направлением на скважину при фиксированном расстоянии от вершины сектора до центра скважины.
Это исследование проводится на основании формулы (17) путем последовательной смены значений углов α при фиксированном значении ρ =1000 метров.
| α, град | Qm, кг/с |
| 0 | 0 |
| 3 | 162,03 |
| 6 | 168,97 |
| 9 | 173,25 |
| 12 | 176,34 |
| 15 | 178,74 |
| 18 | 180,67 |
| 21 | 182,24 |
| 24 | 183,53 |
| 27 | 184,59 |
| 30 | 185,45 |
| 33 | 186,13 |
| 36 | 186,65 |
| 39 | 187,01 |
| 42 | 187,22 |
| 45 | 187,29 |
| 48 | 187,22 |
| 51 | 187,01 |
| 54 | 186,65 |
| 57 | 186,13 |
| 60 | 185,45 |
| 63 | 184,59 |
| 66 | 183,53 |
| 69 | 182,24 |
| 72 | 180,67 |
| 75 | 178,74 |
| 78 | 176,34 |
| 81 | 173,25 |
| 84 | 168,97 |
| 87 | 162,03 |
| 90 | 0 |
Далее на основании полученных данных строиться диаграмма, визуально отражающая зависимость дебита скважины от угла α.
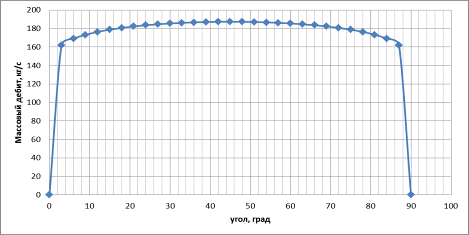
Рис.5 – зависимость дебита газовой скважины в прямоугольном секторе от угла между непроницаемой границей и направлением на скважину
-
Исследование зависимости дебита газовой скважины от расстояния между вершиной сектора и центром скважины при фиксированном значении угла α между непроницаемой границей и направлением на скважину.
Это исследование также проводится на основании формулы (17) при фиксированном значении α=300
| ρ, м | Qm, кг/с |
| 200 | 139,43 |
| 500 | 162,37 |
| 1000 | 185,45 |
| 2000 | 216,18 |
| 3000 | 239,39 |
На основании этих данных построим график зависимости дебита скважины в зависимости от расстояния между вершиной сектора и центром скважины при фиксированном значении угла α.
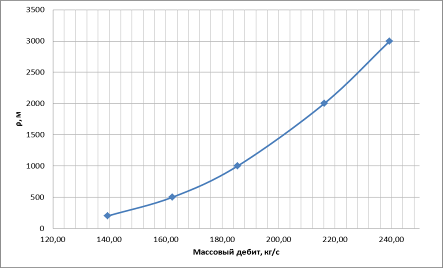
Рис.6 – зависимость дебита скважины в прямоугольном секторе от расстояния между центром скважины и вершиной сектора
4.2 Распределения давления вдоль луча, проходящего через вершину сектора и центр скважины
-
Сравним дебиты газовой скважины расположенной в круговом пласте и прямоугольном секторе на удалении ρ=1000 метров от вершины и α=300.
Подставляя исходные данные в формулы (17) и (18), получим:
Qm_круг=246,58 кг/м3
Qm_сектор=185,45 кг/м3
-
Найдем распределение давление вдоль луча, проходящего через вершину сектора и центр скважины, а также через центр кругового пласта и скважину.
Расчет давлений ведется по формулам (19) и (20).
| Распределение давления | ||||||
| в секторе | | в скважине | ||||
| R, м | Р, МПа | | R, м | Р, МПа | ||
| 1 | 13,04 | | 1 | 14,38 | ||
| 100 | 13,04 | | 100 | 14,34 | ||
| 200 | 13,03 | | 200 | 14,29 | ||
| 400 | 13,01 | | 400 | 14,18 | ||
| 400 | 13,01 | | 400 | 14,18 | ||
| 600 | 12,96 | | 600 | 14,02 | ||
| 700 | 12,91 | | 700 | 13,91 | ||
| 800 | 12,82 | | 800 | 13,74 | ||
| 900 | 12,64 | | 900 | 13,45 | ||
| 950 | 12,42 | | 950 | 13,16 | ||
| 970 | 12,26 | | 970 | 12,94 | ||
| 990 | 11,88 | | 990 | 12,44 | ||
| 995 | 11,63 | | 995 | 12,12 | ||
| 999 | 11,03 | | 999 | 11,34 | ||
| 999,9 | 10,09 | | 999,9 | 10,13 | ||
| 1000,1 | 10,09 | | 1000,1 | 10,13 | ||
| 1001 | 11,03 | | 1001 | 11,34 | ||
| 1005 | 11,64 | | 1005 | 12,12 | ||
| 1010 | 11,89 | | 1010 | 12,44 | ||
| 1030 | 12,29 | | 1030 | 12,94 | ||
| 1050 | 12,48 | | 1050 | 13,16 | ||
| 1100 | 12,74 | | 1100 | 13,46 | ||
| 1200 | 13,02 | | 1200 | 13,75 | ||
| 1300 | 13,20 | | 1300 | 13,92 | ||
| 1500 | 13,45 | | 1500 | 14,13 | ||
| 1700 | 13,64 | | 1700 | 14,26 | ||
| 2000 | 13,87 | | 2000 | 14,41 | ||
| 2300 | 14,05 | | 2300 | 14,52 | ||
| 2600 | 14,21 | | 2600 | 14,60 | ||
| 3000 | 14,39 | | 3000 | 14,70 | ||
| 4000 | 14,73 | | 4000 | 14,87 | ||
| 5000 | 15 | | 5000 | 15 | ||
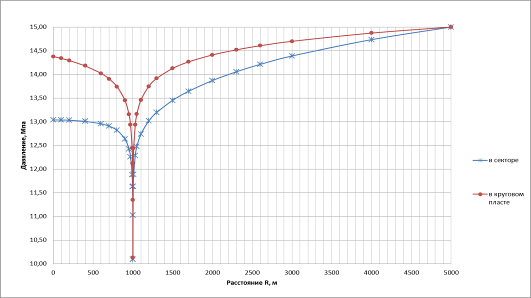
Рис.7 – распределение давления при ρ = 1000 и = 30
5. Практическое использование полученных результатов
Полученные результаты открывают возможность воздействия и контроля за дебитом скважины на основе определения угла между непроницаемой границей и направлением на скважину α, и расстоянии между центром скважины и вершиной сектора.
Заключение. Выводы и рекомендации
Исходя из поставленной задачи, была изучена методика расчета движения газа в пористой среде. На примере решения задачи, рассматривающей совместную работу газовой скважины, расположенной в прямоугольном секторе, ограниченном сбросами, были изучены особенности движения газа в скважинах, а также влияние координат скважины внутри сектора на продуктивность скважин. В результате были получены аналитические зависимости дебита от угла между непроницаемой границей и направлением на скважину α при движении жидкости (газа) в скважине.
Из графиков зависимости дебита газовой скважины, расположенной в прямоугольном пласте, от угла между непроницаемой границей и направлением на скважину α, и от расстояния между вершиной сектора и центром скважины ρ, следует, что дебит скважины будет максимальным при угле α равным 450 и расстоянии ρ стремящемся радиусу контура питания. При этом, темп изменения дебита скважины, приходящееся на один градус, не постоянен.
Из графика распределения давления в круговом пласте и прямоугольном секторе, ограниченном сбросами, видно, что для добывающей скважины в секторе линии равного потенциала не являются окружностями, следовательно и линии тока не будут представлять собой прямые линии. Таким образом, процессы фильтрации газа в круговом пласте и в секторе принципиально отличаются.
Список использованных источников
-
Закиров С.Н, Лапук Б.Б. Проектирование и разработка газовых месторождений. – М.:Недра,1974. – 373с. -
Пыхчаев Г.Б., Исаев Р.Г. Подземная гидравлика. – М.: Недра, 1973. – 360с. -
Кравченко М.Н., Разбегина Е.Г. Прикладные задачи теории фильтрации. – М.: РГУ нефти и газа им. И.М. Губкина, 2003. – 83с;