тәуелді. Бірақ Шредингер теңдеуінен электронның күйін анықтайтын меншікті функция мәндері үш кванттық сандармен анықталады: n- бас кванттық сан, l – орбитальдық кванттық сан және m – магниттік кванттық сан. Барлық кванттық сандар - функциясының қасиеттерінін анықталады.

Орбиталды (немесе азимуталды) кванттық сан электронның орбиталды импульс моментін анықтайды

. (12.2)

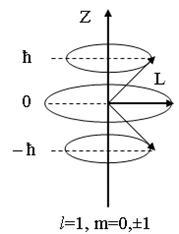
12.2 сурет

Бас кванттық санның берілген мәндерінде саны мәндерін қабылдай алады.

Кванттық механикада орбиталды импульс моментінің өзіне тән қасиеттерге ие: бірмезгілде импульс моментінің және оның проекцияларының бірі (мысалы, ) берілуі мүмкін, қалған екі проекциясы анықталмаған.

Магниттік кванттық сан орбиталдық импульс моментінің кеңістіктің таңдап алынған бағытындағы проекциясын анықтайды

. (12.3)

Орбиталды кванттық санның берілген мәндерінде ол мәндеріне ие болады.

Импульс моментінің проекциясының бүтін сандығын ( бірлікте) кеңістіктің таңдап алынған бағытындағы импульстік моменттің бағдарлануының квантталуымен түсіндіруге болады (12.2 суретті қараңыз). Сонымен Шредингер теориясы бойынша сутегі атомындағы электронның күйі үш кванттық сандармен анықталады. Әрбір меншікті мәнге, энергиядан басқа, орбиталды және магниттік кванттық сандары әртүрлі бірнеше меншікті функциялар сәйкес келеді. Яғни ол сутегі атомы бірнеше әртүрлі күйде энергияның бір мәніне ие бола алатынын білдіреді. 12.1 кестеде алғашқы екі энергетикалық деңгейлерге сәйкес келетін күйлер көрсетілген.

Энергиялары бірдей күйлер азғындалған күй, қандай да бір энергия мәнінде әртүрлі күйлердің саны, энергетикалық деңгейге сәйкес келетін азғындалу еселігі деп аталады. Кванттық және сандарының мүмкін мәндері үшін азғындалу еселігін есептеу қиын емес

. (12.4)

12.1 к е с т е

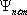
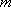
					Азғындалу еселігі
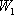
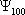
		1	0	0	1
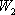
		2	0 1 1 1	0	4
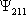
				+1
				0
				-1

12.3 Сутегі атомының оптикалық спектрі

Сутегі атомының оптикалық спектрі (электромагнитті сәуле шығару спектрі) қарапайым. Ол атомның энергетикалық спектріндегі энергетикалық деңгейлерге сәйкес келетін жағдайлармен байланысты жиілік шкаласы жағдайындағы бірнеше жеке спектрлі сызықтардан тұрады

,

мұндағы - қозған күй энергиясы;

- қозған немесе негізгі күй, және де .

Сутегі атомының спектрінің негізгі ерекшелігі, бұл спектр заңдылықпен топталған сызықтар сериясынан тұрады. Есептеулер нәтижелері эксперименттермен жақсы сәйкес келеді.

12.4 Электрон спині

Шредингер теориясында кванттық бөлшектердің кеңістіктегі орнын сипаттаудан өзгеше еркіндік дәрежелері ескерілмейді. Осы қосымша еркіндік дәрежелерге байланысты моментті бөлшектің спині деп аталады. Спин – классикалық физикада аналогы жоқ кванттық шама. Спин –масса немесе заряд сияқты кванттық бөлшектің ішкі қасиеті.

---

Спиннің болуы және оның барлық қасиеттері салыстырмалы теория талаптарын қанағаттандыратын кванттық механикадағы Дирактың теңдеуінен шығады. Спин сонымен қатар протон, нейтрон, фотон және басқа элементар бөлшектерде де болады( мезондардан басқа).

Электронның меншікті импульс моментінің модулі кванттық механиканың жалпы заңы 1/2-ге тең спиндік кванттық санмен анықталады.

. (12.5)

Спиннің орбиталды моменттен маңызды ерекшелігі спиннің абсолютті мәнінің сақталуы. Оның тек берілген бағыттағы проекциясы ғана өзгеруі мүмкін

, . (12.6)

Сонымен, сутегі атомындағы электрон күйі төрт кванттық сандармен n,l,m және m_s толық анықталады. Энергияның меншікті мәніне ( -ден басқа) орбиталды және магниттік кванттық сандары өзгеше бірнеше меншікті функциялар сәйкес келеді.

Электронның спині болғандықтан азғындалу дәрежесі (12.4) тағы екі есеге көбейеді.

13 Дәріс. Кванттық статистика және оны қолдану

Дәрістің мақсаты:

- Паули принципін меңгеру;

- Бозе-Эйнштейн және Ферми-Дирак үлестірулерімен танысу.

13.1 Ұқсас бөлшектердің ажыратылмаушылығы. Паули принципі

Ұқсас бөлшектерің үлкен санынан тұратын кванттық жүйенің классикалық жүйеден елеулі ерекшіліктері болады. Кванттық физикадағы бұл ерекшелік микробөлшектердің табиғатымен, яғни олардың толқындық қасиеттері болғандығымен түсіндіріледі.

Кванттық теорияға сәйкес барлық микробөлшектер екі кванттық статистикаға бағынатын, екі класқа бөлінеді.

- жартылай спинді бөлшектер, оларды фермиондар және олар Ферми-Дирак статистикасына бағынады;

- бүтін спинді бөлшектер - бозондар және олар Бозе-Эйнштейн статистикасына бағынады.

Екі кванттық статистика белгілі бір шарттарда жуықтап классикалық Больцман статистикасына өтеді.

Барлық үш статистикада да микрокүйлер тең ықтималды деп есептелінеді. Олардың айырмашылықтары микрокүйлерді және статистикалық салмақтарын анықтау әдістерінде. Классикалық статистикада жүйедегі жеке бөлшектердің қозғалыстарын, олар ұқсас бөлшектер болса да, әрқашан бақылауға болады. Кванттық физикада бөлшектер жүйесінің теориясында ұқсас бөлшектердің ерекше қасиеттері - ұқсас бөлшектердің ажыратылмаушылық принципі деп аталады. Ол былай тұжырымдалады: берілген квантық-механикалық жүйедегі барлық бірдей бөлшектер толығымен ұқсас болады. Екі кванттық статистикалардың физикалық табиғаттарының ерекшеліктері, яғни ұқсас бөлшектердің күйін сипаттайтын - толқындық функциясының симметриялы және антисимметриялы екі типі осы ажыратылмаушылық принципінен шығады.

Толқындық функцияның симметриялы және антисимметриялы болуы олардың өзара әсерлесуіне тәуелсіз, бөлшектің спинімен анықталады.

Фермиондардың ерекшелігі: олар Паули принципіне бағынады. Паули принципі: ұқсас фермиондардан тұратын кез келген кванттық-механикалық жүйеде бір күйде тек қана бір фермион бола алады.

---

Бозе-Эйнштейн статистикасында әрбір кванттық күйде бірнеше бөлшектер бола алады.

Статистикалардың айырмашылықтары 13.1 суретте көрсетілген.

Суретте Больцман статистикасында барлық микрокүй төртеу, олардың әрқайсысының ықтималдылығы 1/4 .Екі кванттық статистикада алғашқы екі күй ұқсас. Ферми-Дирак статистикасында соңғы екі күй мүмкін емес (Паули принципі бойынша). Тек бір ғана микрокүй қалады, табылу ықтималдылығы 1-ге тең.

13.1 сурет

13.2 Кванттық үлестірілулер

Кванттық статистиканың негізгі есебі – барлық бөлшектер жүйесінің ең ықтимал күйін сипаттайтын параметрлердің орташа мәнін анықтау және осы параметрлерге сәйкес таралу функцияларын табу.

Бөлшектердің энергия бойынша кванттық үлестірілуін қарастырамыз. Бұл үлестірілу энергиясы бір күйдегі бөлшектердің орташа санын анықтайтын, функция түрінде жазылады

Фермиондар үшін , (13.1)

Бозондар үшін , (13.2)

мұндағы – химиялық потенциал.

Бұл үлестірулердің ерекшеліктері:

– фермиондар үшін функциясының мәні бірден артық болмауы керек, ал бозондар үшін кез келген мән бола алады;

– бозондар үшін (13.2) өрнектегі мәні оң сан болуы мүмкін емес;

– егер болса, онда екі үлестірілудің де алымдарындағы бірлікті ескермеуге болады және формула Болцман үлестірілуіне өтеді

, (13.3)

мұндағы – нормалау коэффициенті.

Бұл жағдайда бөлшектердің түрі өзгермейді (бозон бозон болып, фермион фермион болып қалады), формула сәйкес келеді.

13.3 Металдардағы электрондар үшін Ферми-Дирак үлестірілуі

Классикалық электронды теорияда металдардың көптеген қасиеттері еркін электрондар моделімен түсіндіріледі. Кванттық физикада еркін электрондары жуықтап тік бұрышты потенциалды шұңқырдағы фермиондардан тұратын идеал газ ретінде қарастыруға болады. Электрондардың энергетикалық спектрі дискретті, бірақ энергетикалық деңгейлері тығыз орналасқандықтан оларды квазиүздіксіз деп алуға болады. Абсолют нөл температурадағы электронды газды қарастырамыз.

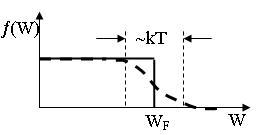
13.2 сурет

Бұл жағдайда

, егер ,

, егер .

Суретте (13.2 суретке қараңыз) тұтас сызықпен f функциясының сызбасы көрсетілген. Сызбада энергиясы барлық күйлер толтырылған, ал энергиясы күйлер бос. Қарастырылып отырған жағдайда шамасын Ферми энергиясы немесе Ферми деңгейі деп атайды. Ферми энергиясы - жағдайда металдардағы еркін электрондардың энергиясының максимал мәні

, (13.4)

мұндағы - электрон массасы; - металдағы электрондардың концентрациясы.

Металдар үшін: ≈ 5 эВ. Еркін электрондардың орташа энергиясы есептеулер бойынша

. (13.5)

Классикалық газдарда мұндай орташа энергияға ~ температура сәйкес келер еді. Бұл температура кез келген металдың балқу температурасынан бірнеше есе артып кетеді. Ферми деңгейіндегі электрондардың жылдамдығы шамасында.

Электронды газдың мұндай күйі (13.2 суреттегі сызбасының тұтас қисық) толығымен азғындалған газ деп аталады.

---

Ферми-Дирак үлестірілуі жағдайда еркін элетрондар мен атомдардың жылулық қозғалысының әсерлесу салдарынан Ферми деңгейінен (13.2 суреттегі сызбасының пунктирлі қисық) асып кетеді. Асып кету аймағы шамамен жылулық қозғалыстың kT энергиясымен шамалас. Сондықтан тек Ферми деңгейіне жанасып жатқан ең жоғарғы деңгейлердегі электрондар ғана өзінің энергияларын өзгерте алады.

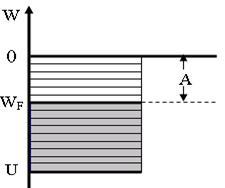
13.3 сурет

Электронды газ потенциалды шұңқырда орналасқан деп алып, электрондардың үлестірілуін қарастырамыз.

A

Мұндағы -потенциалды шұңқырдың тереңдігі. – Ферми деңгейі, бұл деңгейден төменгі аймақ еркін электрондармен толтырылған, ал электрондардың металдан шығу жұмысының жаймасы стрелкамен көрсетілген.

Суретте көрсетілгендей, электрондардың металдан шығу жұмысы классикалық физикадағыдай, потенциалды шұңқырдың түбінен бастап емес, электрондармен толтырылған ең жоғарғы энергетикалық деңгейден бастап есептелінеді екен.

Ферми энергиясы температураға тәуелді болғандықтан, шығу жұмысы да температураға тәуелді болады. Электрондардың кинетикалық энергиясы потенциалды шұңқырдың түбінен бастап есептелінеді.

Металлдардың электр өткізгіштігінің кванттық теориясы классикалық электронды теориядан алынған

.

Меншікті электр өткізгіштік өрнегі

. (13.6)

Бұл өрнек те классикалық теориядан алынған өрнекке ұқсағанымен одан едәуір айырмашылығы бар. Өрнектің алымындағы орташа жылулық жылдамдықтың орнында – электроны бар жоғарғы энергетикалық деңгейдегі электрон жылдамдығы тұр. Бұл жылдамдық металдың температурасына тәуелді емес. Толқынның кристалдық тор түйіндерінен шашыраусыз өтуінің орташа қашықтығы - . Ол жүздеген тор периодына тең болуы мүмкін. Температураның артуына байланысты электронды толқындардың тордың жылулық тербелістерінен шашырауы артуы мүмкін, сондықтан шамасы азаяды. Бөлме температурасында шамасы температураға кері пропорционал ~ , ол тәжірибе нәтижесімен сәйкес келеді.

Кванттық және классикалық статистикалардың айырмашылықтары төменгі температурада және электрондардың үлкен концентрациясында, яғни азғындалған күйде айқын байқалады. Металдағы электронды газ тығыздығы өте үлкен , тіпті кәдімгі температурада да бұл газ азғындалған күйде болады.

14 Дәріс. Қатты денелердің аймақтық теориясы

Дәрістің мақсаты:

- қатты денелердің аймақтық теориясын оқып үйрену;

- шалаөткізгіштердің өткізгіштік қасиетімен танысу.

14.1 Кристалдардағы электрондардың энергетикалық спектрінің аймақтық құрылымы

Металдардағы еркін (нөлдік жуықтау) электрондар металдардың электр өткізгіштігін және басқа қасиеттерін жақсы түсіндіреді, бірақ басқа қатты денелердің осы қасиеттерге неге ие бола алмайтынын түсіндіріп бере алмайды.

Кристалда электрондар тордың периодтық өрісінде қозғалады деп қарастырылады. Бұл жағдайда электрондардың энергияларының мүмкін мәндерінің спектрлері кезектесіп орналасқан рұқсат етілген және тыйым салынған аймақтарға топталады.

---

Энергетикалық аймақтардың пайда болуын атомдық дискретті деңгейлердің кристалл тордағы атомдардың әсерлесуінен жіктелетіндігімен түсіндіруге болады. Электрондар Паули принципіне бағынатындығы әсерлесуші атомдардың бірдей энергетикалық күйлерінің мүмкін болмайтындығына әкеліп соғады.

Әрбір рұқсат етілген аймақ бір-біріне жақын орналасқан деңгейлерден тұрады. Олардың саны кристалдағы атомдар санына тең. Рұқсат етілген энергетикалық аймақтар тыйым салынған аймақпен бөлінген. Тыйым салынған аймақта энергетикалық деңгейлер болмайды.

Кристалдағы атомдардың энергетикалық деңгейлерінің жіктелінуі 14.1 суретте көрсетілген. Паули принципі бойынша электрондар рұқсат етілген энергетикалық аймақтардың ең төменгі деңгейінен бастап, әртүрлі күйлеріне таралып орналасады.

Сонымен, кристалдарда электрондардың энергетикалық спектрі аймақтық құрылымға ие болады. Аймақтар ені кристалдың өлшеміне тәуелсіз. Кристалдағы атомдар саны неғүрлым көп болса, аймақтағы деңгейлер соғұрлым жиірек орналасады. Рұқсат етілген аймақ ені бірнеше электрон-вольтқа тең. Егер кристалдағы атомдар саны болса, аймақтағы деңгейлер ара қашықтығы шамамен болады. Әрбір энергетикалық деңгейде спиндері қарама-қарсы екі электрон бола алады.

14.1 сурет

14.2 Металлдардағы, диэлектриктердегі және шалаөткізгіштердегі энергетикалық аймақтар

Атомдардың белгілі бір қасиеттеріне байланысты рұқсат етілген аймақ арасында ені ΔW болатын тыйым салынған аймақ болады, немесе көршілес аймақтар қабаттасып кетеді (14.2 суретті қараңыз). Атомдардың валенттік электрондары рұқсат етілген аймақтардың бірінде толығымен немесе жартылай толып орналасуы мүмкін. Бұл аймақ валенттік аймақ деп аталады. Одан жоғары бос аймақтар орналасқан.

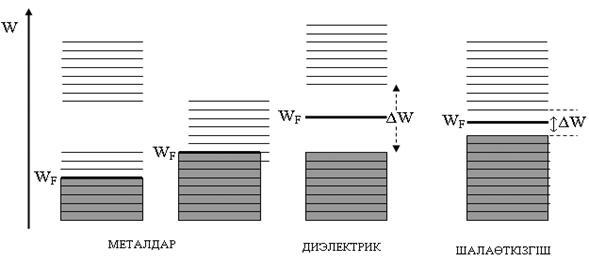
14.2 сурет

Кристалдардың өткізгіштігі ондағы электрондардың энергетикалық спектрінің аймақтық құрылымына және температурада осы спектрдің электрондармен толуына байланысты. Осы қасиеттер арқылы кристалдардың металл, диэлектрик немесе жартылай өткізгішіке жататынын анықтауға болады.

Толтырылған және жартылай толтырылған аймақтардағы электрондардың қасиеттері әртүрлі. Егер аймақ электрондармен жартылай толтырылған болса, әлсіз электр өрісінің өзі осы аймақ ішіндегі электрондарды бос күйлерге өткізе алады. Электрондар қозғалысының орташа жылдамдығы нөлден өзгеше болып, кристалда электр тоғы пайда болады. Сондықтан кез келген жартылай толтырылған аймақ өткізгіштік аймақ болып табылады.

Егер Т=0 К кезінде валенттік аймақ толық толтырылған болса, кристалл изолятор немесе шалаөткізгіш болып табылады. Мұндай кристалды қыздырғанда жылулық ауытқу әсерінен валенттік аймақтағы электрондардың қандай да бір бөлігі көршілес бос аймаққа өтіп кетеді. Нәтижесінде екі аймақ та өткізгіштік аймаққа айналады. Егер тыйым салынған аймақтың ені бірнеше электрон-вольт болса, онда мұндай электрондар саны өте аз болады. Сондықтан тыйым салынған аймақтың ені үлкен болатын кристаллдар диэлектриктер деп аталады. Егер кристалдағы тыйым салынған аймақтық ені эВ болса, онда ол температурада шалаөткізгіш болып табылады.

---

Смотрите также файлы

• Физика дәріс.docx

• Философия методичка рус.doc

• Философия.docx

• Электротехникалық материалтану зертаханалық жұмыс 3,4.docx

• Электростатика.doc