2.4 Механикалық жүйе. Сыртқы және ішкі күштер. Ньютон-ның үшінші заңы . Механикалық жүйенің масса центрі және оның қозғалыс заңы

Біртұтас ретінде қарастырылатын материялық нүктелер (денелер) жиынын механикалық жүйе дейді.

Қарастырылып отырған механикалық жүйеге кірмейтін денелерді сыртқы денелер дейді. Жүйеге сыртқы денелер тарапынан әсер ететін күштер сыртқы күштер деп аталады. Ал ішкі күштер дегеніміз қарастырылып отырған жүйеге кіретін бөлшектердің өзара әсерлесу күштері.

Механикалық жүйе сыртқы депнелермен өзара әсерлеспесе (немесе оған сыртқы күштер әсер етпесе) , онда ол тұйықталған немесе оқшауланған жүйе деп аталады.

Материялық нүктелердің (денелердің) бір –біріне әсері өзара әсерлесу сипатта болады. Ньютонның үшінші заңы:

Материялық нүктелердің бір-біріне әсер ету күштері модулі бойынша әрқашан тең, бағыты жағынан қарама-қарсы және осы нүктелерді қосатын түзу бойымен әсер етеді

Ғ_1,2 = - F_2,1. (2.4 )

Бұл күштер әр материялық нүктеге түсірілгені, әрқашан жұбымен әсерлеседі және табиғаты бір болып табылады. Ньютонның үшінші заңы жеке материялық нүктелер динамикасынан кезкелген материялық нүктелер жүйесі динамикасына өтуге мүмкіндік береді, үйткені кезкелген өзара әсерлесуді материялық нүктелердің жұпталып өзара әсерлесуі ретінде қарастыруға болады.

Механикада массаның жылдамдыққа тәуелді еместігіне байланысты жүйенің импульсын оның масса центрі импульсымен өрнектеуге болады. Материялық нүктелер жүйесінің масса центрі (немесе инерция центрі) дегеніміз орны осы жүйенің бүкіл массасы орналасқан ойша алынған С нүктесі болып табылады. Оның радиус-векторы (немесе координаттары):

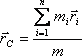(2.5 )

мұндағы m_і және r_і - сәйкес і-інші материялық нүктенің мас-сасы мен радиус-векторы;

n - жүйе ішіндегі материялық нүктелер-дің саны; m=∑m_{і -} жүйенің массасы. Бұл жағдайда жүйенің импульсы:

. (2.6 )

Масса центрінің қозғалыс заңы: жүйенің масса центрі жүйенің массасы түгелдей жинақталған материялық нүктенің қозғалысы сияқты, ал оған әсер ететін күш жүйеге әсер ететін барлық сыртқы күштердің геометриялық қосындсына тең болады.

. ( 2.7 )

3 дәріс. Қатты дененің айналмалы қозғалыс динамикасы

Дәрістің мақсаты:

- қатты дененің қозғалыс параметрлері ұғымын енгізу;

- қатты дененің айналмалы қозғалыс заңдары мен теңдеулерін оқып үйрену.

3.1 Күш моменті мен импульс моменті. Материялық нүкте үшін моменттер теңдеуі

Қозғалмайтын О нүктесіне қатысты Ғ күшінің моменті деп О нүктесінен күштің А түсу нүктесіне жүргізілген радиус-вектор мен Ғ күштің векторлық көбейтіндісімен анықталатын физикалық шама:

. ( 3.1 )

3.1 Сурет

Күш моменті күштің денені нүктеге қатысты айналдыру қабілетін сипаттайды. О нүктесіне бекітілген дене күштің әсерінен моменттің бағытымен сәйкес келетін осьті айналады (3.1 суретті қара).

---

Бөлшектің О нүктесіне қатысты импульс моменті деп О нүктесінен күштің А түсу нүктесіне жүргізілген радиус-вектор мен Р импульстың векторлық көбейтіндісіне

, (3.2)

тең шаманы айтады,

мұндағы – берілген уақыт мезетіндегі бөлшектің радиус-векторы;

– оның импульсі ( ).

Импульс моментінің векторы және векторлары жатқан жазықтыққа

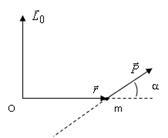
3.2Сурет

перпендикуляр болады (3.2 суретті қара).

3.2 Механикалық жүйе үшін моменттер теңдеуі

Бөлшектер жүйесінің импульс моменті жүйенің барлық бөлшектерінің импульс моменттерінің векторлық қосындысына тең

( ұқсас). (3.4)

(3.2) теңдеуінен уақыт бойынша туынды алып, күш моментінің бөлшектің импульс моментінің өзгеру жылдамдығы арқылы анықталатынын көруге болады

. (3.5)

(3.5) қатынасы моменттер теңдеуі деп аталады.

3.3 Қатты дененің қозғалмайтын осьті айналуы. Қатты дененің осьті айнала айналмалы қозғалысы динамикасының негізгі теңдеуі. Инерция моменті. Штейнер теоремасы

Бекітілген Oz осін қатты дене айналып қозғалады делік. Денеге күш түсірілген. Oz осіне қатысты күш моменті деп О нүктесіне қатысты күш моментінің М_z проекциясын айтады. Ол берілген күштің берілген осьті айналдыру қабілетін сипаттайды және

, (3.6)

тең болады,

мұндағы l – R sin-ға тең күшінің иіні;

– оське перпендикуляр жазықтықта осьтен күш түсірілген нүктеге дейін жүргізілген радиус-вектор;

– күштің осы жазықтыққа жүргізілген проекциясы.

Дененің оське қатысты импульс моментін анықтау үшін осы дененің барлық бөлшектерінің О нүктесіне қатысты қорытқы импульс моментінің осы оське проекциясын алу қажет (3.3 суретті қара)

. (3.7)

(3.7 ) өрнегін мына түрге оңай түрлендіруге болады:

, (3.8) (3.9)

шамасын оське қатысты дененің инерция моменті деп атайды. Инерция моменті дене массасының осьті айнала орналасуына тәуелді және айналмалы қозғалыс кезіндегі дененің инерттілік қасиетін сипаттайды. Осылайша,

, немесе . (3.10)

(3.10) –ды ескере отырып, (3.4) және (3.5) –тен

, (3.11)

3.3 Сурет

мұндағы – Z осіне қатысты денеге түсірілген барлық күштің моменті;

– берілген оське қатысты дененің инерция моменті;

– айналып қозғалған дененің бұрыштық үдеуі.

(3.1 1) өрнегі қозғалмайтын оське қатысты айналып қозғалған қатты дененің айналмалы қозғалысының динамикасының негізгі заңын береді.

4 дәріс. Энергия және жұмыс

Дәрістің мақсаттары:

- энергия, жұмыс, қуат ұғымдарын меңгеру;

- энергияның әр түрін есептеу әдісін меңгеру.

4.1 Энергия - қозғалыс пен өзара әсерлесудің барлық түрлерінің универсал өлшеуіші

Материяның қозғалыс формалары өте көп. Оның ішіндегі ең қарапайымы – механикалық қозғалыс. Оны сандық түрде сипаттау үшін біз импульс ұғымын енгіздік. Жылулық қозғалыстың сандық сипаттамасы – температура болса, электр өрісінің сипаттамасы - кернеулік және т.б. Бұл шамалардың барлығы материяның әртүрлі қозғалыс формаларының сапалық ерекшеліктерін көрсетеді. Сондықтан материяның барлық қозғалыс формаларына қатысты және олардың өзара түрленуін көрсететін физикалық шаманы енгізу қажет. Физикадағы ортақ ұғымдардың бірі - энергия - осындай физикалық шама болып табылады.

---

Энергия - материяның әртүрлі қозғалыс формаларының ортақ өлшеуіші.

Қозғалыс материяның ажырамас бөлігі болғандықтан, кез келген жүйе энергияға ие болады. Жүйенің энергиясы жүйеде мүмкін болатын өзгерістерді (сандық және сапалық) сандық түрде сипаттайды. Энергия –күй функциясы.

Табиғатта механикалық қозғалыс арқылы энергиясы бір денеден басқа денеге берілетін процестер үздіксіз жүріп тұрады. Дененің механикалық қозғалысының өзгерісін оған басқа денелер тарапынан әсер етуші күштер тудырады. Өзара әсерлесуші денелер арасындағы энергия алмасу процесін сандық түрде сипаттау үшін берілген денеге түсірілген күштің жұмысын қарастырады. Жұмыс–энергияның күштік өзара әсерлесу процестерінде өзгеру шамасы.

4.2 Күштің жұмысы. Қуат

Массасы m қандай да бір бөлшекті қарастырайық. Оған күшпен әсер етейік. Осы бөлшек үшін Ньютонның екінші заңының теңдеуі

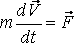. (4.1)

(4.1) теңдеуін бөлшектің шексіз аз орын ауыстыру векторына көбейтсек ( = екенін ескереміз)

. (4.2)

4.1 суреттен скаляр көбейтіндісі

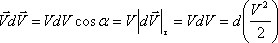
тең болады.

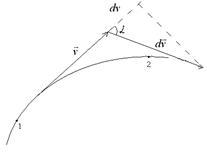
4.1 Сурет

Онда,

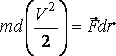. (4.3)

(4.3) –тің оң жағындағы шама күштің dA жұмысы деп аталады.

, (4.4)

мұндағы α – күш пен орын ауыстырудың арасындағы бұрыш.

(4.4) формуласы күштің элементар жұмысын сипаттайды. Дене шекті қашықтыққа орын ауыстырғанда атқарылатын толық жұмыс қозғалыс траекториясы бойымен алынған қисық сызықты интеграл бойынша анықталады.

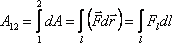. (4.5)

Күш жұмысы – алгебралық шама, ол оң да, теріс те, нөлге де тең болуы мүмкін. Жұмыстың графиктік түрде анықталуы 4.2 суретте көрсетілген.

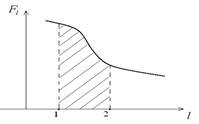
4.2 Сурет

Бірлік уақыт ішінде істелінген жұмысқа тең физикалық шама қуат деп аталады

. (4.6)

4.3 Бөлшектің және бөлшектер жүйесінің кинетикалық энергиясы

(4.3) теңдеуінің сол жағын қарастырайық. Ол қандай да бір функцияның толық дифференциалын береді.

. (4.7)

W_k шамасы бөлшектің кинетикалық энергиясы деп аталады. Кинетикалық энергия – толық энергияның бөлшектің қозғалысымен байланысты бөлігі. Тыныштықта тұрған дененің (V=0) кинетикалық энергиясы болмайтынын ескерсек, (4.7 )-дан

(4.8)

тең екені шығады.

4.4 Қатты денелер айналғандағы кинетикалық энергия және жұмыс

Қозғалмайтын осьті айналып қозғалған қатты дененің айналмалы қозғалысы кезіндегі кинетикалық энергиясы

. (4.9 )

(4.8 ) және (4.9 ) өрнектері релятивистік емес (v<<c) бөлшектер үшін дұрыс болады. (4.8 ) өрнегі бөлшекке бірнеше күш әсер еткен жағдайда да дұрыс болып табылады. Онда А₁₂ - барлық күштердің жұмыстарының қосындысы. Олай болса, бөлшектің кинетикалық энергиясының өзгерісі осы бөлшекке әсер етуші барлық күштердің жұмысына тең болады.

А₁₂=W_k2-W_k1 . (4.10)

Дене Ғ күштің әсерімен dφ аз бұрышқа бұрылғанда күштің түсу нүктесі ds= r dφ жол жүреді де істелген жұмыс

dA = F sin φ r dφ = M_z dφ . (4.11)

4.5 Консервативті және консервативті емес күштер. Бөлшектің потенциалдық энергиясы және оның өріс күшімен байланысы

Барлық күштерді физикалық табиғатына тәуелсіз консервативті және консервативті емес күштер деп екі топқа бөледі. Егер күштің жұмысы бөлшектің бастапқы нүктеден соңғы нүктеге қандай траекториямен орын ауыстырғанына байланысты болмаса, ондай күштер консервативті күштер деп аталады

---

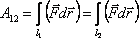. (4.12)

Егер орын ауыстыру тұйықталған жолмен өтсе, консервативті күштің жұмысы нөлге тең болады

. (4.13 )

Орталық (гравитациялық, кулондық) күштер, ауырлық күші, серпімділік күші консервативті күштерге жатады.

Консервативті емес күштің жұмысы орын ауыстыру өтетін жолға тәуелді болады. Консервативті емес күштерге үйкеліс күштері, ортаның кедергі күші жатады. Үйкеліс күшінің жұмысы әрқашан теріс болады. Мұндай күштер диссипативті деп аталады.

Кеңістіктің әрбір нүктесінде бөлшекке бір нүктеден екінші нүктеге заңдылығымен өзгеретін күш әсер ететін кеңістіктің аймағын күш өрісі деп атайды. Күш өрістері векторлық болып табылады. Күш өрісі біртекті (ауырлық күшінің өрісі) және орталық (гравитациялық өріс) болып бөлінеді. Консервативті күштер өрісі ерекше қасиеттерге ие, олар потенциалды өрістер класын құрайды. Әр нүктедегі өрісті кеңістіктегі нүктенің орнына және күштің сипатына тәуелді болатын қандай да бір W_p( ) функциясымен сипаттауға болады. Олай болса, бөлшек 1 нүктеден 2 нүктеге орын ауыстырғанда консервативті күштің жұмысы W_p функциясының кемуіне тең болады

A₁₂ =W_p1 –W_p2 =-∆W_p . (4.14)

W_p функциясы сыртқы консервативті өрістегі бөлшектің потенциалдық энергиясы деп аталады. Мұндай өрісте жұмыс потенциалдық энергия есебінен жасалатынын (4.14) теңдеуінен көруге болады.

Бөлшектің потенциалдық энергиясы W_p( ) өрісті тудыратын объектілермен өзара әсерлесу энергиясы болып табылады. (4.14) формуласы әрбір нақты жағдайда W_p үшін (кез-келген тұрақтыға дейінгі дәлдікпен) өрнегін алуға мүмкіндік береді.

Потенциалды өрісте орналасқан бөлшектің энергиясы мен күштің арасындағы байланысты анықтайық. Ол үшін элементар жұмыстың формуласын жазамыз

. (4.15)

күштің кез келген l бағытқа проекциясы

. (4.16)

Орын ауыстыру бағыты ретінде x, y, z координат осьтері бойындағы бағыттарды аламыз

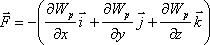, (4.17)

немесе

. (4.18)

(4.18) формуласы потенциалды өрістегі энергия мен күштің арасындағы байланысты өрнектейді.

5 дәріс. Сақталу заңдары

Дәрістің мақсаттары:

 механикадада орын алатын сақталу заңдарының мағынасын түсіндіру;

 олардың тұжырымдалуы мен қолдану шектерін меңгеру

 сақталу заңдарына ортақ және айырмашылықта болатын жағдайлар.

5.1& Денелердің тұйықталған жүйесі. Импульстің сақталу заңы

Импульстің, импульс моментінің және энергияның сақталу заңдары басқа заңдардан өздерінің жалпыға бірдейлігімен ерекшеленеді.

Табиғаттың осы негізгі заңдары тек классикалық механикада ғана емес, релятивтік физика мен кванттық механикада да орындалады.

Барлық сақталу заңдары алғашында бірнеше эксперименттік фактілерді жалпылау ретінде тәжірибелік жолмен ашылған. Кейін, олардың сақталу заңдарының өзара байланысы түсіндірілді және қандай шарттар орындалғанда олар өзінің формасын өзгерте алатынын көрсетуге болатыны анықталды.

---

Импульстің сақталу заңы - кеңістіктің біртектілігін көрсететін табиғаттың жалпы заңы. Кеңістіктің біртектілігі дегеніміз кеңістіктің барлық нүктелерінде оның қасиеттерінің бірдей болуы.

Импульстің сақталу заңы тұйықталған жүйелерде орындалады. Егер жүйе сыртқы күш өрісінде болса, онда ол үшін кеңістіктің әртүрлі аймақтары эквивалентті болмайды.

Сыртқы күштер әсер етпейтін жүйе (өзара әсерлесуші денелердің жиынтығы) оқшауланған немесе тұйықталған жүйе деп аталады..

Материялық нүктелердің (денелердің) тұйықталған жүйесінің толық импульсі уақыт бойынша өзгермейді

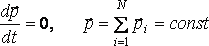. (5.1)

5.2 Импульс моментінің сақталу заңы

Айналмалы қозғалыс динамикасының негізгі заңын қорытқан кезде, біз қатты денені материялық нүктелер жиынтығы деп қарастырып, мынадай қорытындыға келдік

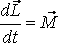, (5.2)

мұндағы –жүйенің импульс моменті;

– жүйеге әсер ететін сыртқы күштердің қорытқы моменті.

Ішкі күштердің моменттерінің қосындысы кез келген жүйе үшін нөлге тең.

Егер сыртқы күштер болмаса (тұйықталған жүйеде), онда , сондықтан, .

(5.3)

Тұйықталған жүйенің материялық нүктелерінің (денелер) толық импульс моменті тұрақты болып қалады.

Егер дене қозғалмайтын осьті айналып қозғалса, , онда . екенін ескерсек ,

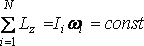. (5.4)

Импульс моментінің сақталу заңы да импульстің сақталу заңы сияқты табиғаттың негізгі заңы болып табылады. Оның негізінде кеңістіктің изотроптылығы қасиеті жатыр, яғни тұйық жүйенің бұрылуы оның механикалық қасиеттеріне әсер етпейді.

5.3 Механикадағы энергияның сақталу заңы. Энергияның сақталуының және түрленуінің жалпы физикалық заңы

Энергияның сақталу және айналу заңы табиғаттың негізгі заңдарының бірі болып табылады. Энергияның сақталу заңы уақыттың біртектілігін көрсетеді, яғни уақыттың барлық кезеңдері үшін бірдей. Уақыттың әр кезеңдерінің эквивалентті болу себебі кез келген физикалық процесс оның қашан басталғанына тәуелсіз бірдей жүріп отырады. Энергияның сақталу және айналу заңының терең мағынасы бар. Ол қозғалыстың материяның ажырамас қасиеті екенін, оның пайда болмайтынын және жоғалмайтынын, бір түрден екінші түрге айналатынын көрсетеді.

Бөлшек пен бөлшектер жүйесінің толық механикалық энергиясын қарастырайық. (4.7) формуласына оралайық. Бөлшекке консервативті және консервативті емес күштер әсер етеді делік. Онда

W_k2–W_k1=A₁₂^*+A₁₂

A₁₂^*=W_p1–W_p2 екенін ескерсек,

(W_k2+W_p2)–(W_k1+W_p1)=A₁₂ (5.5)

Бөлшектің толық механикалық энергиясы W кинетикалық және потенциалдық энергияларының қосындысына тең. Консервативті күш өрісіндегі бөлшектің толық механикалық энергиясының өзгерісі бөлшекке әсер ететін консервативті емес күштердің жұмысына тең

W₂–W₁=A₁₂ . (5.6)

N өзара әсерлеспейтін бөлшектер жүйесінің энергиясы осы жүйені құрайтын бөлшектердің барлық энергияларының қосындысымен анықталады

. (5.7)

Егер бөлшектер бір-бірімен өзара әсерлесетін болса, аддитивті болып табылмайтын олардың өзара әсерлесу энергиясын ескеру қажет.

---

Смотрите также файлы

• Физика дәріс.docx

• Философия методичка рус.doc

• Философия.docx

• Электротехникалық материалтану зертаханалық жұмыс 3,4.docx

• Электростатика.doc