Добавлен: 02.02.2019
Просмотров: 13136
Скачиваний: 101
10.2 Гейзенбергтің анықталмағандық қатынасы
Классикалық механикада кез келген бөлшек белгілі бір траекториямен қозғалатын болса, онда кез келген уақыт мезетінде оның координатасы мен импульсін анықтауға болады. Классикалық бөлшектен айырмашылығы микробөлшектердің толқындық қасиеттері бар екенінде. Негізгі айырмашылығы микробөлшектердің траекториясы хаостық, ал оның координатасы мен импульсінің дәл мәнін анықтау мүмкін емес.
Бұл корпускулалық-толқындық дуализмнен шығады. Мысалы, бір нүктедегі толқын ұзындығы деп айтуға болмайды, оның физикалық мағынасы жоқ, ал импульс толқын ұзындығына тәуелді шама, осыдан, микробөлшектің импульсі белгілі болса, координатасы белгісіз және керісінше, микробөлшектерінің координатасының дәл мәні белгілі болса, онда оның импульсі белгісіз болады.
Мысалы,
электрон үшін координата
мен
импульс компонентінің
дәл
мәнін анықтау мүмкін емес.
пен
анықталмағандықтары
төмендегі қатынасты қанағаттандырады
.
(10.3)
Аналогиялық
түрде (10.3) қатынасын
пен
,
пен
үшін
де және энергия мен уақыт үшін де жазуға
болады
.
(10.4)
(10.3) и (10.4) қатынастары анықталмағандық қатынастары деп аталады. Анықталмағандақ қатынастарын бірінші рет 1927 ж. В.Гейзенберг орнатты.
Бұл қатынастардың физикалық мағынасы төмендегідей: микроәлем объектісі координаталары мен импульс проекцияларының дәл мәні анықталатын күйде бола алмайды.
(10.4)
формулаға сәкес энергияны
дәлдікпен
өлшеу үшін
уақыт
қажет. Мысал ретінде сутегітектес
атомдардың энергетикалық деңгейлерінің
(негізгі деңгейден басқа деңгейлер) дәл
мәнінің болмауын келтіруге болады. Бұл
спектрлік сызықтардың кеңеюіне әкеліп
соғады және оны барлық қозған күйдегі
өмір сүру
с
уақытымен түсіндіруге болады. Сонымен
бірге, егер жүйе тұрақты болмаса
(радиоактивті ядро), онда өмір сүру
уақытының шекті болуына байланысты
оның энергиясы
-дан
аз емес статистикалық дәлдікпен
анықталады
,
(10.5)
мұндағы
–
жүйенің өмір сүру уақыты.
Мұндай сипаттама классикалық механикадағы бөлшек қозғалысының сипатттамаларынан өзгеше болады, себебі классикалық механикада бөлшек белгілі траекториямен қозғалады және әрбір нүктедегі координатасы мен импульсі белгілі. Екі түйіндес айнымалының анықталмағандық мәндерінің көбейтіндісі Планк ħ тұрақтысынан аз болмайды деген тұжырым Гейзенбергтің анықталмағандық принципі деп аталады.
Гейзенбергтің анықталмағандық принципі кванттық механикадағы фундаменталды қағидаларының бірі болып табылады және корпускулалық-толқындық дуализммен байланысты.
10.3 Де Бройль толқындарының статистикалық түсіндірмесі
Электрондардың дифракциясы бойынша жасалған тәжірибелердің нәтижелерін корпускулалық түсініктер тұрғысынан түсіндіріп көрейік. Дифракциялық құрылғыдан өтетін бөлшектердің саны аз болса, электрондар түсетін фотопластинкадағы нүктелер ешқандай заңдылықпен таралмайды. Біраз уақыттан соң ғана жекелеген нүктелер бір-біріне жалғасып дифракциялық көрініс байқала бастайды. Тәжірибені қайталайтын болсақ, дәл осындай нәтиже аламыз. Бірақ тәжірибе жасағанда келесі бөлшектің қай нүктеге түсетінін дәл айту мүмкін емес, өйткені қозғалыстың классикалық траекториясы жоқ. Бірақ тәжірибенің статисткалық нәтижесін болжай аламыз. Осыдан тәжірибелер санын арттырып, микробөлшектердің қозғалыс заңдылығының статистикалық сипаттамасын алуға болады. Ал жекелеген бөлшекке келетін болсақ, оның фотопластинканың белгілі нүктесіне түсу ықтималдылығы туралы ғана сөз қозғай аламыз.
Статистикалық түсінік бойынша, кеңістіктің белгілі бір нүктесіндегі де Бройль толқынының интенсивтілігі бөлшектің осы нүктеден табылу ықтималдылығына тура пропорционал. Мұндай түсінік микробөлшектің құрылымын қарастырмайды. Дәл классикалық физикадағы сияқты, бөлшек дискретті болып табылады.
11 Дәріс. Шредингер теңдеуі және оның шешімдері
Дәрістің мақсаты:
- Шредингер теңдеуінің шешімін табу;
- туннельдік эффект құбылысымен танысу.
11.1 Кванттық механикадағы бөлшектердің күйі. Толқындық функция
Кез келген фундаменталды физикалық теорияның құрылымында күй түсінігі және күй динамикасын түсіндіретін теңдеулер маңызды элементтер болып табылады.
Классикалық
механикада бөлшектер күйі берілген
уақыт мезетінде x,
y, z
координаттармен
,
,
импульстермен
беріледі, ал динамиканың негізгі теңдеу
- Ньютонның екінші заңы. Микродүние
физикасында бөлшектер күйінің мұндай
анықтамасы және күй функциясы болып
табылатын күштер түсінігі мүлдем
мағынасын жоғалтады.
Бөлшектердің толқындық қасиеттерінің болуы микробөлшектердің күйін, толқындық қасиеті бар қандай да бір функция көмегімен түсіндіруге болатынын айқындайды.
Кванттық
механикада микробөлшектердің күйі
кеңістіктік координаттар және уақыт
функциясы болып табылатын
толқындық
функциямен беріледі. Релятивистік емес
жағдайда бұл күйдің уақыт бойынша
өзгеруі, яғни микробөлшектердің динмикасы
кванттық теориялардың негізгі теңдеуі
- Шредингер теңдеуімен сипатталады.
Толқындық
функция математикалық мағынада өріс
(ол комплексті болғандықтан
функциясымен
сипатталатын толқындар байқалмайды)
болып табылады. Толқындық функцияның
физикалық мағынасының түсініктемесін
алғаш рет М. Борн берді, ол төменде
келтірілген.
комплексті
функциясының
модулының
квадраты координаттары x,y,z болатын
нүкте айналасындағы
көлемде
бөлшектердің болу ықтималдығының
тығыздығын береді. Микробөлшектерді t
уақыт мезетінде осы көлем ішінде болу
ықтималдығы келесі өрнекпен беріледі
.
(11.1)
функциясы
өзінің мағынасы бойынша қандай да бір
шарттарды қанағаттандыруы қажет.
Толқындық функция барлық жерде үздіксіз
және бірмәнді
болуы керек. Сонымен қатар (11.1) өрнегімен
анықталатын ықтималдық толқындық
функцияның нормалдау шартына сәйкес
бірге тең болуы тиіс.
.
(11.2)
Келтірілген шарттардың кванттық механикада үлкен мәні бар. Шредингер теңдеуінің шешімдері осы талаптарды тек белгілі бір шарттарында ғана, мысалы энергияның белгілі бір дискретті мәндерінде ғана қанағаттандырады.
11.2 Шредингер теңдеуі
Толқындық функция микробөлшектер күйінің негізгі сипаттамасы. Кванттық механикада толқындық функция арқылы осы күйдегі берілген объекті сипаттайтын физикалық шаманының орташа мәнін есептеуге болады.
Күйдің уақыт бойынша өзгеруі, яғни микробөлшектер динамикасы,
релятивистік емес жағдайда, кванттық теориялардың негізі болып табылатын Шредингердің стационар емес теңдеуімен сипатталады
,
(11.3)
мұндағы
-
жорамал бірлік;
-
бөлшек массасы;
-
Лаплас операторы;
-
микробөлшектің
потенциалдық энергиясы.
Бұл теңдеуді қандай да бір классикалық физиканың заңдарынан қорытылып шығарылмайды. Классикалық физикада Ньютонның екінші заңы қандай рөл атқарса, релятивистік емес кванттың механикада Шредингер теңдеуі дәл сондай рөл атқарады.
Кванттық механикада микробөлшек стационар күш өрісінде орналасқан және оның потенциалдық энергиясы уақытқа тәуелді емес болатын, стационар есептер көптеп кездеседі. Бұл жағдайда Шредингердің стационар теңдеуі қолданылады
.
(11.4)
Бұл
теңдеудегі
параметрінің
мағынасы бөлшектің толық энергиясы, ал
бұл теңдеудің
шешімі
кеңістіктік координатар функциясы
болып табылады. Шредингер теңдеуі дербес
туындылы теңдеу және оның шешімі үшін
бастапқы және шекаралық шарттар берілуі
қажет.
Берілген
жағдайда,
(11.4) теңдеуін қанағаттандыратын
функциясы
меншікті
функция,
ал теңдеудің шешімінен шығатын
энергия
мәндері меншікті
мәндер
деп аталады.
11.3 Шредингер теңдеуін шешу мысалдары
11.3.1 Бірөлшемді шексіз терең потенциалдық шұңқырдағы микробөлшектің күйі.
Массасы
m
бөлшек Ох
осі бойымен ғана қозғалсын. Бөлшектің
қозғалысы шұңқырдың қабырғаларымен
шектеулі, қабырғалардың координаталары
x=0
және x=L.
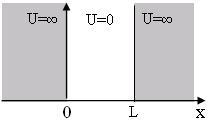
Мұндай өрістегі бөлшектің потенциалдық
энергиясы 11.1 -
суретте көрсетілген. Бөлшектің
функциясы
х
координатасына ғана тәуелді болғандықтан,
Шредингердің (11.4) стационарлық теңдеуі
мына түрде жазылады
(11.5)
Бөлшек
шұңқырдан шыға алмайды, сондықтан
және
аймақтарда
.
Пси-функцияның үздіксіздік шартынан
шығатыны, шұңқырдың шекараларында ол
нөлге тең болуы қажет
11.1 сурет
.
(11.6)
Шекаралық
шарт -
(11.6) теңдеуі (11.5) теңдеуіне қосымша.
Шұңқырдың шектерінде (бұл аймақта
)
(11.5) өрнегі мына түрде жазылады
.
(11.7)
Бұл
теңдудің шешімін табу дегеніміз,
бөлшектің
(знергетикалық
спектр) толық энергиясының мүмкін
мәндерін және осы мәндерге сәйкес
келетін
толқындық
функциясын табу.
Жоғарыдағы (11.7) теңдеуі – тербелістер теориясындағы белгілі теңдеу. Ол (11.6) шартты энергияның мына мәндерінде қанағаттандырады
,
(11.8)
мұндағы
-
бүтін сандар.
Бұл
нәтиже микробөлшектің потенциалдық
шұңқырдағы энергетикалық спектрі
дискретті және бөлшек энергиясы
квантталатынын көрсетеді. Ал
энергияның
кванттық мәндері -
энергия
деңгейлері,
n-бас
кванттық сан
деп аталады.
Бөлшектің меншікті функциясы (11.8) өрнегіне сәйкес,
,
.
(11.9)
Нормалау
(11.2)
шартынан
коэффициенті
табылады,
11.2 сурет
және (11.9) өрнегі мына түрде жазылады
.
(11.10)
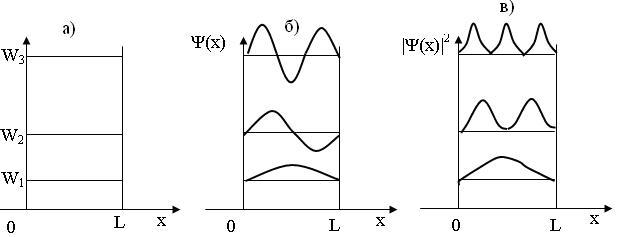
Бөлшектің
потенциалдық шұңқырдағы энергетикалық
деңгейлері 11.2 –суретте (а), сонымен
қатар
функциясының
сызбасы (б) және координатасы х
нүкте айналасында бөлшектің болуының
(в)-
ықтималдық тығыздығының сызбалары
келтірілген.
Кванттық
және классикалық бөлшектердің
айырмашылықтары 11,2- суретте сипатталған.
Классикалық бөлшек шұңқырда кез-келген
энергияға ие бола алады және шұңқыр
түбіндегі тыныштықтағы бөлшек үшін
.
Ал кванттық бөлшек спектрі дискретті,
оның ең аз энергиясы n=1
мәніне сәйкес келеді және ол нөлге тең
болмайды. Кванттық бөлшек тыныштықта
боуы мүмкін емес. Классикалық бөлшек
шұңқырдың кез келген нүктесінде болу
ықтималдығы бірдей. Кванттық бөлшектің,
мысалы ең төменгі n=1
энергетикалық деңгейде шұңқырдың
ортаңғы бөлігінде болу ықтималдығы ең
жоғары болады, ал шұңқырдың шет жағында
кез-келген деңгейде бөлшектің табылу
ықтималдығының тығыздығы нөлге тең.
11.3.2 Туннельдік эффект.
Туннельдік
эффект – классикалық физиканың заңдарына
қайшы келетін, кеңістіктің аймақтарынан
микробөлшектердің өтіп кетуі. Бөлшектің
(бірөлшемді)
х
осі бойымен тікбұрышты қарапайым
потенциалдық тосқауылдан өтуін
қарастырамыз (11.3 суретті қара). Егер
бөлшектердің
толық
энергиясы потенциалдық тосқауылдың
биіктігінен
аз болса, онда
нүктесінде
ол шағылады. Шредингер теңдеуінен
шығатыны
аймақта
бөлшектің бөгеттен өту ықтималдығы
нөлден
өзгеше.
Бөгеттің сол жағында түскен және шағылған
толқын, ал оң жағында тек өткен толқын
болады. Бөгет ішінде
-функциясы
толқындық сипатта болмайды, ықтималдылық
экпоненциалды кемиді.
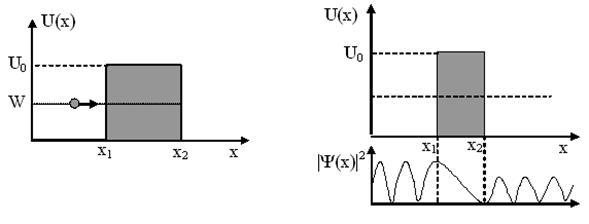
11.3 сурет
Туннельдік эффект арқылы металдардағы электрондардың суық эмиссиясын, альфа ыдырауын, ядролардың спонтанды бөлінуін және т.б. түсіндіруге болады.
11.3.3 Гармоникалық осциллятор.
Сызықты гармоникалық осцилятор - квазисерпімді күштің әсерінен бір өлшемді қозғалыс жасайтын жүйе. Ол классикалық және кванттық теория есептерінде қолданылады. Кванттық гармоникалық осцилятордың потенциалдық энергиясы
.
(11.11)
Мұндағы
-
бөлшек массасы;
-
тербеліс жиілігі және қозғалыс х
осі
бойымен болады.
К
ванттық
осциллятор үшін Шредингер теңдеуін
шешу күрделі математикалық есеп.
Кванттық гармоникалық осцилятордың тек энергетикалық спектрін ғана қарастырамыз
(11.12)
мұндағы
–
кез келген теріс емес бүтін
11.4 сурет сан.
Осцилятордың
энергетикалық спектрі (11.12) өрнегінен
дискретті екені шығады және энергияның
ең төменгі мәні
.
Бұл кванттық осциллятордың негізгі
деңгейі. Көршілес екі деңгейлер аралығы
-кванттық
санға тәуелсіз, яғни бірдей ( 11.4 суретке
қараңыз ).
Сонымен
негізгі деңгей
болса,
онда кванттық осцилляторды тоқтату
мүмкін емес. Мысалы
абсалютті нөл температурада да кристалл
тордағы атомдардың тербелісі тоқтамайды.
Кванттық тербелістің ең аз энергиясы
нөлдік энергия деп аталады
11.4 Бордың сәйкестік қағидасы
Кванттық сандар үлкен болғанда кванттық механика нәтижелері классикалық нәтижелермен сәйкес келу керек.
Мысалы, потенциалдық шұңқырдырдағы көршілес екі энергетикалық деңгейлер интервалын бағалаймыз. Көршілес екі деңгейлер энергияларының айырмасы
.
(11.13)
Интервалдың
шамасы
кванттық
санның артуына байланысты сызықты
артады.
Жоғарыда
келтірілген (11.8) және (11.13) өрнектерінен
қатынасын
табамыз.
,
n1
жағдайда
.
(11.14)
Алынған
нәтижелерден
кванттық
санның артуына байланысты көршілес
энергия деңгейлердің
ара
қашықтығы бөлшектің энергиясымен
салыстырғанда азаятынын шығады. Бұл
жағдайда энергетикалың спектрдің
дискреттілігін ескермеуге болады, яғни
кванттық сипаттаулар классикалыққа
жақындайды (11.2, в суретке қараңыз).
Ықтималдылық тығыздығының амплитудалық
мәні
-ге
тең, барлық
үшін
бірдей. Кванттық санның артуына байланысты
функциясының
түйіндері артады,
-нің
үлкен
мәндерінде
қисықтың максимум және минимумдары бір
- біріне өте жақын орналасады, бөлшектердің
координаталарын дәл емес өлшеу кезінде
суреттер тұтасып кетеді және біз
классикалық нәтижеге өтеміз.
12 Дәріс. Сутегі атомы үшін Шредингер теңдеуінің шешімі
Дәрістің мақсаты:
- сутегі атомы үшін Шредингер теңдеуінің шешімін табу;
- спин ұғымымен танысу.
Кванттық физиканың маңызды жетістіктерінің бірі қарапайым атомдардың спектрін, сонымен қатар химиялық элементтер қасиеттеріндегі периодтылықты толық жете түсіндіруі болды.
Сутегі атомы бір протоннан және бір электроннан тұрады. Электрон кулондық күштің электростатикалық өрісінде орналасқан және оның потенциалды энергиясы әсерлесуші бөлшектердің e зарядымен және олардың r арақашықтығымен анықталады
.
(12.1)
Осы жағдай үшін Шредингер теңдеуінің негізгі шешімдерін қарастырамыз.
12.1 Сутегі атомының энергетикалық спектрі
Шредингер теңдеудің шешімі келесі жағдайларда ғана үздіксіз, бірмәнді және шекті болады:
-
.
Бұл аймақта кез келген энергия күйі -
энергетикалық спектрі тұтас, толқындық
функциясының күйі еркін бөлшектің
күйіне жақын болады.;
-
.
Нәтиже классикалықтан өзгеше
болады-электрон энергиясы квантталады.
Энергетикалық спектр оң бүтін
бас
кванттық сандарға сәйкес келетін
дискретті
энергетикалық деңгейлерден тұрады.
Кванттық сан артқан сайын деңгейлер
арасы жиіленеді,
шекті
мәніне
энергия
сәйкес келеді (12.1 суретте
потенциалды
шұңқырдағы электронның энергетикалық
деңгейлері көрсетілген).
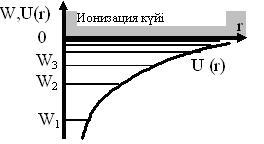
12.1 сурет
Электронның
энергиясы
ең
аз мәнге ие болатын күйі негізгі күй
деп аталады және ол стационар болып
табылады. Ал
күйлердің
барлығы қозған күй деп аталады. Қозған
күйге өту күйі – еріксіз процесс. Атом
қозған күйде белгілі бір
уақытта ғана бола алады, содан кейін ол
негізгі күйге (немесе энергиясы аз басқа
күйге) өздігінен (спонтанды) өтеді. Ол
атомның энергия жұтуы арқылы жүреді.
Атом осы кезде өзінен квант түрінде
электромагнитті сәуле шығарады.
12.2 Орбиталды және магнитті кванттық сандар
Сутегі
атомындағы электрон энергиясы тек
бас
кванттық санға ғана