Бұл кезде дене мен сәуле шығарудың энергия таралуы әрбір толқын ұзындығы үшін өзгеріссіз қалады, ал дене мен қабырға арасындағы кеңістіктегі сәуле шығару тығыздығы берілген температураға сәйкес белгілі бір мәнге жетеді.

Қыздырылған денемен статикалық тепе-теңдікте болатын қуыстағы сәуле шығару тепе-теңдіктегі жылулық сәуле шығару деп аталады. Кез келген басқа сәуле шығару статистикалық тепе-теңдікте болмайды. Себебі олар атомдардың хаостық жылулық қозғалысына тәуелді емес. Жылулық емес сәуле шығару тепе-тең емес.

Жылулық сәуле шығарудың спектрі кейбір жиіліктегі интенсивтілігі максимум болатын тұтас спектр.

Кез келген дененің жылулық сәуле шығаруы төмендегі шамалармен сипатталады. Энергиялық жарқырау – сәуле шығаратын дененің бірлік бетінен барлық бағытта ( бұрыш шамасына) шығарылатын толық энергия ағынына тең шама:

. (8.1)

Дененің бірлік беті арқылы жиілік интервалында шығарылатын энергия ағынының бөлігі дененің сәуле шығару қабілеті деп аталады

. (8.2)

Сәуле шығару қабілеті сәуле шығарудың энергиясының жиілікке тәуелді таралу функциясы болып табылады. Энергетикалық жарқырау мен сәуле шығару қабілеті бір-бірімен байланысты:

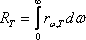. (8.3)

Енді дене бетінің ауданына сәуле ағыны түссін. Осы ағынның бір бөлігін дене жұтады, екінші бөлігі шағылады. Шағылған энергияны өлшемсіз шағылдыру қабілеті деп аталатын шамамен сипаттайды. Ал жұтылған энергияны дененің жұтқыштың қабілеті шамасымен сипаттайды:

, . (8.4)

Онда

. (8.5)

Егер дене түскен сәулелік энергияны толығымен жұтатын болса, мұндай дене абсолют қара дене деп аталады. Барлық жиілікте абсолют қара дене үшін: , . Абсолюттік қара дененің мысалы – кішкене тесігі бар үлкен қуыс дене. Осындай қуыс ішіне енген сәуле оның қабырғасының ішкі бетінен сан рет шағылып, сәуле ең соңында толығымен жұтылады.

Мөлдір емес дененің сәуле шығарғыштың және жұтқыштың қабілеттері арасында мынадай байланыс бар

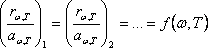. (8.6)

Бұл заңды 1859 жылы Г.Кирхгоф тағайындады. Сондықтан Кирхгоф заңы деп аталады.

Денелердің энергетикалық жарқырауының спектрлік тығыздығының оның жұтқыштық қабілетіне тәуелділігі дене материалына тәуелсіз және барлық денелер үшін бірдей, ол температура мен жиіліктің функциясы болып табылды.

функциясы Кирхгоф функциясы деп аталады. (6) формуладан көріп тұрғанымыздай, бірдей температурада кез келген дененің сәуле шығарғыштық қабілеті абсолют қара дененің сәуле шығарғыштық қабілетінен үлкен болмайды.

8.2 Абсолют қара дененің сәуле шығару заңдары

Абсолют қара дененің жылулық сәуле шығаруын эксперимент жүзінде зерттегенде тәуелділігінің температураға тәуелді екені анықталды (8.1 суретті қара).

Суреттен көрініп тұрғандай, абсолют дененің сәуле шығарғыштық қабілеті температура жоғарылаған сайын күшейе түседі. Температура өскенде сәуле шығару қабілетінің максимумы жоғары жиіліктер аймағына қарай ығысады: ω_{m 1}< ω_{m 2}< ω_{m 3.}

---

Эксперименттен төмендегідей заңдылықтар ашылды:

, (8.7)

, (8.8)

8.1 сурет

мұндағы – Стефан-Больцман тұрақтысы ;

–Вин тұрақтысы .

(8.7) қатынасы Стефан-Больцман заңы деп аталады, ал (8.8) қатынасы Виннің ығысу заңы деп аталады.

8.3 Рэлей-Джинс формуласы. Ультракүлгін апаты

Жылулық сәуле шығару заңдылықтарын Рэлей мен Джинс теориялық түрде түсіндірмек болды. Олар энергияның еркіндік дәреже бойынша таралу туралы классикалық статистика теоремасын қолданды. Тұйық қуыстағы тепе-тең жылулық сәуле шығару қарастырылды. Релей-Джинс заңы

. (8.9)

Рэлей-Джинс теориясындағы абсолют қара дененің энергетикалық жарқырауы болады; мұның физикалық мәні жоқ.

Классикалық физика жылулық сәуле шығаруды жоғары жиіліктер аймағында түсіндіре алмайды. Сәуле шығару теориясындағы бұл жағдай физика тарихында «ультракүлгін апаты» деген атпен белгілі. Осының салдарынан физиканың негізгі теорияларын қайта қарастыруға тура келді.

8.4 Планк формуласы және кванттық гипотеза

Неміс физигі М.Планк бірінші рет Кирхгоф функциясын дұрыс өрнектеді және абсолют қара дененің сәуле шығаруының спектрлік заңдылығының теориясын жасады.

Ол үшін Планк ω жиілікпен тербелетін гармоникалық осцилятордың энергиясын дискретті мән ғана қабылдайды деген гипотеза ұсынды. Энергияның бұл дискретті мәні энергияның элементар порциялары, яғни энергия кванттарының бүтін санына тең:

, (8.10)

мұндағы – универсал тұрақты деп аталады;

– Планк тұрақтысы;

бүтін сандар.

Планктың гипотезасын негізге ала отырып, абсолют қара дененің сәуле шығарғыштық қабілеті үшін төмендегі өрнекті жазуға болады:

. (8.11)

Планк формуласы жиілік интервалдағы барлық эксперименттік нәтижелерді қанағаттандырады. Планк формуласы негізінде Стефан-Болцман және Вин заңдарындағы тұрақтылар есептеліп шығарылды. Планк формуласынан аз жиіліктер аймағында Рэлей-Джинс формуласын алуға болады.

Сонымен, электрмагниттік сәуле шығару корпускулалық сипаты туралы Планк гипотезасы дұрыс деген қорытындыға келдік. Планктың дәл осы идеясы кванттық физиканың дамуына түрткі болды.

9 Дәріс. Электрмагниттік сәуле шығарудың корпускулалық қасиеттері

Дәрістің мақсаты:

- фотонның энергиясын, импульсін есептеп үйрену;

- фотоэффект заңдылықтарын меңгеру;

- Комптон эффектісімен танысу.

Кванттық гипотеза электромагниттік сәулеленудің затпен әсерін зерттегенде, яғни фотоэлектрлік құбылыстарды, Комптон эффектісін, электрон-позитрон жұптарынының туу құбылыстарын зерттегенде жалғасын тапты және эксперимент жүзінде расталды.

9.1 Фотондар

М.Планктың идеясын дамыта отырып, А.Эйнштейн жарық кванттық түрде шығарылады, жұтылады және таралады деп тұжырымдады; яғни жарық дискретті, ол бөлшектерден тұрады. Жарық кванттары фотон деп аталады. Эйнштейн гипотезасына сәйкес фотон энергиясы

, (9.1)

мұндағы – жарық толқынының циклдік жиілігі.

---

Фотон с = 3∙10⁸ м/с жылдамдықпен қозғалады. Фотонның импульсі

, (9.2)

мұндағы – толқындық вектор модулі , ол жарық толқындарының таралу жылдамдығы векторының бойымен бағытталған. Бұл формуланы векторлық түрде жазуға болады

. (9.3)

Фотон энергиясы мен импульсы арасындағы байланыс

. (9.4)

Фотонның массасы

, (9.5)

бірақ басқа бөлшектерден айырмашылығы, фотонда тыныштық масса болмайды .

Сонымен, фотон – электромагниттік сәуле шығару кванты. Басқа бөлшектер сияқты оның энергиясы, импульсы, массасы бар. Фотонның осы корпускулалық сипаттамалары толқындық сипаттамаларымен – жиілікпен және толқындық вектормен байланысқан.

9.2 Фотоэффект

Фотоэффект дегеніміз – электромагниттік сәуле шығару әсерінен электрондардың заттан вакуумге ұшып шығу құбылысы (сыртқы фотоэффект) немесе заттың ішіндегі байланысқан күйдегі электрондардың еркін электрондарға айналу құбылысы (ішкі фотоэффект).

С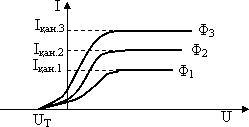 ыртқы фотоэффектіні бірінші рет Г.Герц ашты. Бұл құбылысты А.Столетов 1888 – 1889 жылдар аралығында эксперимент жүзінде жан-жақты зерттеген. Эксперименттен алынған нәтижелер 9.1-суретте көрсетілген, бұл суретте фотоэлементтің вольт-амперлік сипаттамалары келтірілген (бірдей жиілікте ω = const, әртүрлі жарық ағыны үшін фототоктың катод пен анод арасына түсірілген кернеуге тәуелділігі). Графиктен байқайтынымыз:

- болған кезде катодтан шыққан электрондардың бір бөлігі анодқа жетеді. Егер теріс таңбалы тежеуіш кернеу беретін болсақ

9.1 сурет , фототок нольге айналады. Тежеуіш кернеу

жарық ағынына тәуелсіз, ол жарық жиілігімен ғана анықталады;

- кернеудің болатын бір мәнінде фототок қанығу мәніне жетеді I_қан.

Қанығу тогы неғұрлым үлкен болса, жарық ағыны Ф соғұрлым үлкен болады (яғни уақыт бірлігінде көбірек электрондар ұшып шығады);

- катодқа жиілігі әртүрлі жарық түсірейік. Егер жарық жиілігі катодтың материалына тән жиіліктен аз болса, жарық ағынының кез келген мәнінде фотоэффект байқалмайды. жиілік пен оған сәйкес келетін толқын ұзындығы, – фотоэффектінің қызыл шекарасы деп аталады. Заттан электрондардың ұшып шығуы жарықтың толқындық табиғатына қайшы келмейді, бірақ ол фотоэффект заңдылықтарын түсіндіре алмайды.

Фотоэффект заңдарын алғаш рет 1905 ж. А.Эйнштейн түсіндірді. Фотон металл бетіне түскенде өзінің барлық энергиясын электронға береді. Егер бұл энергия үлкен болса, электрон металлдың ішінде ұстап тұрған күшті жеңіп, металдан сыртқа ұшып шыға алады. Бұл процессте энергияның сақталу заңы орындалады:

, (9.6)

мұндағы – – металл бетінен ұшып шыққан электронның максималды жылдамдығы; – электронның металдан шығу жұмысы; –электронның массасы.

(9.6) өрнегі фотоэффект үшін Эйнштейн заңы деп аталады. Бұл формула фотоэффектінің барлық заңдылықтарын түсіндіреді:

- егер сәулелену интенсивтілігі өте жоғары болмаса, онда әрбір фотоэлектрон бір фотонның энергиясын қабылдайды. Бұл кезде электронның максималды жылдамдығы фотонның энергиясына ғана тәуелді;

---

- Фотондардың ағыны тығыздығы фотондардың электрондармен соқтығысу санына байланысты өзгереді. Сондықтан қанығу тогы сәулелену интенсивтілігіне тура пропорционал;

9.3 Комптон эффекті

1922 жылы А.Комптон эксперимент жүзінде рентген сәулелерін еркін электрондар арқылы шашыратқанда олардың жиіліктері екі бөлшектің (фотон мен электронның) серпімді соқтығысу заңына сәйкес өзгеретінін көрсетті.

Комптон тәжірибе жасаған құрылғының схемасы 9.2-суретте көрсетілген.

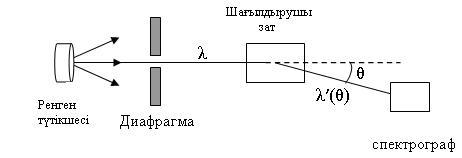
9.2 сурет

Комптон эффектісінің негізгі ерекшелігі: толқын ұзындығы өзгерісі түскен сәуленің толқын ұзындығына да, шашырататын затқа да тәуелді емес, шашырау бұрышымен ғана анықталады.

, (9.7)

мұндағы – тұрақты сан, электронның комптондық толқын ұзындығы деп аталады, .

Комптон эффектісін түсіндіру үшін рентген фотоны мен тыныштықтағы еркін электронның серпімді соқтығысуын қарастырамыз. Атомдағы электронның байланыс энергиясы фотонның электронға беретін энергиясынан (әлдеқайда) біршама кіші.

Энергиямен импульстың сақталу заңдарын жазсақ

, (9.8)

, (9.9)

мұндағы и – рентген фотонының соқтығысуға дейінгі және одан кейінгі энергиялары;

– электронның соқтығысуға дейінгі энергиясы;

- электронның соқтығысудан кейінгі энргиясы;

– соқтығысудан кейінгі электрон импульсі;

и - соқтығысудан кейінгі және одан кейінгі фотон импульсі.

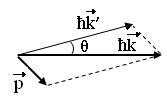
(9.9) теңдеу 9.3-суретте векторлық диаграмма түрінде көрсетілген.

Осы диаграмманы қолданып, (9.9) теңдеуді скалярлық түрде жазамыз

,

9.3 сурет мұндағы

. (9.10)

(9.10) формула Комптон тәжірибелерінің нәтижелерімен сәйкес келеді. Бұл электрмагниттік сәуле шығарудың корпускулалық қасиеті туралы түсініктің дұрыс екенін көрсетеді.

9.4 Электрмагниттік сәуле шығарудың корпускулалық-толқындық дуализмі

Эксперименттен алынған барлық мәліметтер жиынтығынан мынадай қорытынды жасаймыз. Жарық нақты физикалық объект болып табылады. Жарықты кейбір жағдайларда бөлшек түрінде қарастыруға болады, ал басқа жағдайларда толқын түрінде қарастыруға болады.

Физикалық объект бір мезгілде корпускулалық және толқындық қасиеттерге ие болса, онда мұны корпускулалық-толқындық дуализмі деп атайды.

Корпускулалық-толқындық дуализмді классикалық ұғымдармен түсіндіре алмаймыз, себебі фотонды әрбір уақыт мезетінде кеңістікте белгілі бір орын алатын нүктелік объект деп қарастыруға болмайды. Жеке фотонды электр өрісінің кернеулігімен сипаттауға болмайды.

Фотон дегеніміз – электромагниттік сәуле шығарумен байланыста болатын физикалық объект, ол энергиямен және импульспен сипатталады.

10 Дәріс. Зат қасиеттерінің корпускулалық-толқындық дуализмі

Дәрістің мақсаты:

- зат қасиеттерінің корпускулалық-толқындық дуализмін оқып үйрену;

- Де Бройль гипотезасымен танысу.

Классикалық физикада бөлшек пен толқынның табиғатын әртүрлі деп қарастырады. Бөлшек дискретті, кеңістікте өте аз көлем алады, ал толқын болса кеңістікте өте үлкен орын алады.

---

Толқын бір ортадан екінші ортаға өткенде жартылай сынып, екінші ортада таралады, ал жартысы шағылып, интерференциаланады. Бөлшек болса біртұтас, ол интерференциаланбайды.

Бірақ ХІХ ғ. 20-жылдарында физикада табиғаттың фундаментальды заңы ашылды, ол заттың корпускулалық-толқындық дуализмі деп аталады, мұнда бөлшек пен толқын туралы түсініктер біріктірілді.

10.1 Де Бройль гипотезасы

Бөлшек пен толқын дуализмін бірінші рет француз ғалымы Луи де Бройль 1924 жылы тұжырымдады.

Де Бройль идеясы бойынша, дуализм тек оптикалық құбылыстарға ғана тән емес, оның универсалды мәні бар, яғни корпускулалық-толқындық қасиеттер тек қана фотонмен бірге, барлық бөлшектерде болады; мысалы, электронда да болады.

Сонымен Де Бройль теориясы бойынша кез келген микрообъектінің бір жағынан корпускулалық сипаттамалары болады: энергия , импульс , екінші жағынан толқындық сипаттамалары болады: жиілік , толқын ұзындығы . Кез келген бөлшектің корпускулалық-толқындық сипаттамалары дәл фотонның сипаттамалары сияқты байланысқан:

, . (10.1)

Еркін қозғалатын бөлшек ретінде қарастырылатын толқын де Бройль толқыны деп аталады.

Кез келген бөлшектің W энергиясы оның импульсіне р тәуелді . Бұл тәуелділік әр бөлшек үшін әр түрлі, (себебі әр бөлшектің табиғаты әр түрлі, мысалы релятивистік емес бөлшек үшін ).

Кез келген толқынның жиілігі оның толқындық векторына тәуелді; Бұл тәуелділік дисперсия заңы деп аталады. Бұл заң әрбір толқын үшін әртүрлі жазылады.

Сонымен, энергиясы өте жоғары емес қозғалыстағы электронға немесе кез-келген бөлшекке толқын ұзындығы

(10.2)

болатын толқындық процесс сәйкес келеді. Мұндағы және – бөлшектің массасы мен жылдамдығы.

Механикадағы макроскопиялық денелердің толқындық қасиеттері байқалмайды. Мысалы, массасы 1 г дене 10 м/с жылдамдықпен қозғалса, оған сәйкес де Бройльдық толқын ұзындығы . Қазіргі уақытта элементар бөлшектер физикасында м-ге дейінгі арақашықтықта эксперимент жасауға болады, одан аз қашықтықты бақылай алмаймыз. Сондықтан макроскопиялық дененің толқындық қасиетін ескермейміз. Микроскопиялық бөлшектер үшін, мысалы, энергиясы 10 эВ-тан эВ-қа дейінгі электрон үшін Бройль толқынының ұзындығы ≈ м, бұл рентген сәулелерінің толқын ұзындығының диапозоны болып табылады. Сондықтан мұндай электрондардың толқындық қасиеттері рентген сәулелерінің дифракциясы байқалатын кристалдармен шашыратқанда көрінеді.

Де Бройль гипотезасын америка ғалымдары К.Девиссон мен Л.Джемер эксперимент жүзінде электрондар ағынының интерференциясын зерттегенде дәлелдеді. П.С. Тартаковский және Г.П. Томсон бір-біріне тәуелсіз электрондардың металл фольгадан өткен кездегі дифракциясын бақылады. Л.М. Биберман, Н.Г. Сушкин и В.А. Фабрикант (1949 ж.) тәжірибелерінде толқындық қасиеттер микробөлшектер ағынына емес, жекелеген микробөлшектерге тән екенін дәлелденді.

---

Смотрите также файлы

• Физика дәріс.docx

• Философия методичка рус.doc

• Философия.docx

• Электротехникалық материалтану зертаханалық жұмыс 3,4.docx

• Электростатика.doc