. ( 5.8)

Егер жүйе бөлшектерінің арасында сыртқы күштер болмай (A₁₂ =0), тек қана консервативті күштер әсер етсе (мұндай жүйені консервативті деп атайды), (5.7) формуладан көретініміздей, оның толық механикалық энергиясы сақталып қалады. Бұл тұжырым толық механикалық энергияның сақталу заңы болып табылады. Толық механикалық энергия тек денелердің тұйықталған консервативті жүйесінде ғана сақталады.

Импульстің, импульс моментінің және энергияның сақталу заңдары - қуатты және тиімді зерттеу аспабы. Сақталу заңдарының осы қасиеті мынадай себептерге байланысты:

- сақталу заңдары бөлшектердің траекториясына, әсер етуші күштердің сипатына тәуелсіз. Сондықтан, қозғалыс теңдеулерін қарастырмай-ақ, әртүрлі механикалық процестердің қасиеттері жөнінде жалпы және маңызды қорытындылар жасауға мүмкіндік береді;

- бұл дәлел әсер етуші күштер белгісіз болған жағдайда (денелердің, молекулалардың соқтығысуы) да сақталу заңдарын қолдануға болатынын көрсетеді.

6 дәріс. Салыстырмалылықтың арнаулы теориясы элементтері

Дәрістің мақсаты:

- салыстырмалылықтың механикалық принципі мен салыстырмалылық -тың арнайы теориясының негізгі принциптерін, олардың салдарларының маңыздылығын түсіндіру;

- салыстырмалылықтың арнаулы теориясының (САТ) постулаттарының мағынасын ашып көрсету;

-Лоренц түрлендірулерінің инварианттарын оқып үйрену

6.1 Салыстырмалылықтың механикалық принципі және Галилей түрлендірулері

Галилейдің салыстырмалылық принципі (салыстырмалылықтың механикалық принципі) табиғаттың негізгі қасиеттерін бейнелейді: инерциялық санақ жүйесінің бірқалыпты түзу сызықты қозғалатынын немесе тыныштықта болатынын осы санақ жүйесінде жүргізілетін механикалық тәжірибелер арқылы көрсету мүмкін емес.

Галилейдің салыстырмалылық принципіне Галилейдің түрлендіру координаттары сәйкес келеді. Егер екі инерциалдық санақ жүйелері осьтері бір-біріне параллель және салыстырмалы қозғалыс олардың біреуінде (мысалы, х осінің бойында) (6.1 суретті қара) өтетін болса, Галилей түрлендірулері (тура және кері) мына түрде болады

6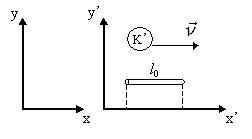 .1 Сурет

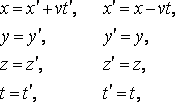( 6.1)

мұндағы – К` жүйесінің шартты түрде қозғалмайтын К жүйесіне қатысты жылдамдығы.

Галилей түрлендіруі кезінде өзгеріссіз қалатын физикалық шамалар Галилей түрлендіруінің инварианттары деп аталады.

Сондай шамалардың бірі - үдеу

(6.2)

,

ү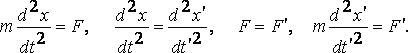 деу Ньютонның екінші заңының да инвариантты екенін көрсетеді

Классикалық механиканың негізгі инварианттарының арасында кеңістіктік интервал (екі кеңістіктік нүктелердің ара қашықтығы)

, (6.3)

және уақыт интервалы орын алады

(6.4)

Классикалық механикада инвариантты емес шамаға жылдамдық жатады. Жылдамдықтарды қосудың классикалық заңы бойынша

. (6.5)

Салыстырмалылық принципі мен Галилей түрлендірулері классикалық механика негізін құрайтын абсолют кеңістік пен абсолют уақыт жайында көріністі бейнелейді.

---

6.2 Салыстырмалылықтың арнайы теориясы постулаттары

Салыстырмалылықтың арнайы теориясы - кеңістіктің біртекті және изотроптылығын, уақыттың біртектілігін бейнелейтін кеңістік пен уақыт жөнінде физикалық теория.

Эйнштейн құрған салыстырмалылықтың арнайы теориясы негізін екі постулат құрайды: салыстырмалылықтың жалпылама принципі және вакуумдегі жарық жылдамдығының тұрақтылық принципі:

-барлық физикалық құбылыстар инерциалдық санақ жүйелерінде бірдей өтеді;

- вакуумдегі жарық жылдамдығы барлық инерциалдық санақ жүйелерінде бірдей және ол жарық көздері мен қабылдағыштардың жылдамдықтарына тәуелсіз, яғни универсал тұрақты болады. Оның шамасы

м/с.

Эйнштейннің негізгі постулаттарының салдарлары:

- уақыт әртүрлі санақ жүйелерінде әртүрлі өтеді. Оқиғаның қай санақ жүйесіне қатысты екені көрсетілгенде ғана екі оқиғаның арасындағы белгілі уақыт аралығы болады деп айтуға болады. Қандай да бір санақ жүйесінде бір мезгілде өтетін оқиғалар басқа санақ жүйелерінде басқаша өтеді.;

- К және К` санақ жүйелеріндегі бір оқиғаның уақыт аралықтарының салыстырмалылығы

(6.6)

Объектімен бірге қозғалған сағат бойынша есептелген уақыт осы объектінің меншікті уақыты деп аталады

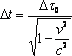
. (6.7)

Қозғалыстағы сағат қозғалмайтын сағатқа қарағанда баяу жүреді. Сағаты тоқтап тұрған жүйеде уақыт жүрісі баяулайды, сағат қозғалысының әсері оның жұмыс істеуіне байланысты емес, ол тек уақыттың салыстырмалылығын көрсетеді. Сонымен, бірегей әлемдік уақыт болмайды. Уақыт, оның жүрісі, бірмезгілділік ұғымдары салыстырмалы.

Кеңістік интервалдарының салыстырмалылығы

(6.8)

Стержень қозғалмайтын жүйедегі санақ жүйесінде өлшенген стерженьнің ұзындығы меншікті ұзындық деп аталады. (6.8)-ден көретініміздей меншікті ұзындықтың шамасы ең үлкен, яғни барлық санақ жүйесінде денелердің ұзындығы меншікті ұзындықпен салыстырғанда қысқарады. Осы құбылыс қозғалыс бағытында дене өлшемдерінің лоренцтік қысқаруы деп аталады. Денелердің геометриялық өлшемдерінің лоренцтік қысқаруы дене өлшемдеріне қозғалыстың физикалық әсеріне байланысты емес. Ол кеңістік аралықтарының абсолют еместігін, оның санақ жүйесіне байланысты екендігін көрсетеді.

6.3 Лоренц түрлендірулері

Салыстырмалылықтың арнайы теориясында кеңістік пен уақыттың қасиеттерін бейнелеуші координата мен уақытты релятивистік түрлендіру Лоренц түрлендірулері деп аталады. Осы түрлендіруге сәйкес, К` жүйеден К жүйеге өту (6.9) формуласы арқылы, ал К жүйеден К` жүйеге өту (6.10) формуласы арқылы жүзеге асады.

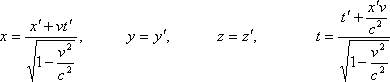, (6.9)

( 6.10)

Координата мен уақыт түрлендірулері негізінде салыстырмалылық принципінің тағы бір тұжырымын беруге болады: физикалық заңдар Лоренц түрлендірулеріне қатысты инвариантты болады.

Лоренц түрлендірулерінің кейбір салдарларын қарастырайық. Бірін-шіден, Лоренц түрлендірулері біздің әлемдегі кеңістік пен уақыттың қасиеттерінің бір-бірінен ажырамас байланысы бар екендігін ашып көрсетеді. Сондықтан, кеңістікті немесе уақытты бөлек қарастыруға болмайды, біздің әлем өмір сүретін кеңістік-уақыт жөнінде айтқан дұрыс болады. Басқаша айтсақ, біздің әлем төрт өлшемді.

---

Екіншіден, Лоренц түрлендірулері негізінде бірмезгілділіктің салыстырмалылығын сипаттауға болады.

Үшіншіден, (6.5) формуласымен берілген жылдамдықтарды қосудың классикалық заңын жарық жылдамдығына жуық жылдамдықпен қозғалған денелер үшін қолдануға болмайды. Х осі бойымен қозғалған бөлшек үшін жылдамдықтарды қосудың релятивтік заңы

( 6.11 )

6.4 Салыстырмалылықтың арнайы теориясының инварианттары

Лоренц түрлендіруі бойынша жарық жылдамдығы барлық санақ жүйелерінде тұрақты. Сондай-ақ, Лоренц түрлендіруі бойынша жарық жылдамдығы максимал жылдамдық болып табылады.

Релятивтік механикада Лоренц түрлендіруіне қатысты кеңістік пен уақыт аралықтарының интервалдарының инварианттығы жөнінде ештеңе айтуға болмайды. Олай болса, салыстырмалылықтың арнайы теориясында екі оқиғаның арасында кеңістік пен уақыт аралықтарымен байланысты Лоренц түрлендіруіне қатысты инвариантты болатын шаманы көрсетуге болмас па еді? Бұл сұрақтың оңай шешімі бар. Салыстырмалылықтың арнайы теориясында төмендегі қатынаспен анықталатын инвариантты шамасы бар.

. (6.12)

Осы шама оқиғалар арасындағы кеңістіктік-уақыттық интервал (немесе жай интервал) деп аталады.

7 дәріс. Релятивтік динамика элементтері

Дәрістің мақсаты:

- релятивтік механика заңдылықтарын оқып үйрену;

- материялық нүктенің негізгі теңдеуін оқып үйрену;

- энергия мен импульс және масса арасындағы байланыстарды талдап оқу.

7.1 Релятивтік импульс. Материялық нүктенің релятивтік динамикасының негізгі теңдеуі

Қозғалыстағы релятивтік бөлшектің ( дененің) m релятивтік массасы оның жылдамдығына байланысты

. (7.1)

мұндағы , m₀ - бөлшектің тыныштық массасы, яғни бөлшек тыныштық күйде болатын инерциалды санақ жүйесінде өлшенген масса.

Релятивистік импульс мына формуламен өрнектеледі

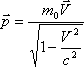. (7.2)

Жүйенің релятивтік импульсы сақталады. Релятивтік импульстың сақталу заңы - кеңістіктің біртектілігінің салдары.

Релятивтік динамиканың негізгі заңы

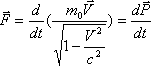. (7.3 )

қатынасымен өрнектелетін динамиканың негізгі заңы (2.2) өрнегін ескерсек, релятивтік қозғалыстар үшін де дұрыс болады.

Жалпы жағдайда, динамиканың релятивтік заңы бойынша және векторларының бағыттары сәйкес келмейді, үдеу мен күш шамалары арасындағы пропорционалдық бұзылады.

7.1 Масса мен энергияның өзара байланыс заңдылығы

Массасы m дененің толық энергиясы деп аталатын =mc² шамасының жанжақты сипаты бар, ол энергиялардың барлық түрлеріне қолданылады, яғни энергиямен, ол қандай түрде болса да, масса байланыста болады ( m=W/c² ) және керісінше кез келген энергия массамен байланыста болады деп тұжырымдауға болады

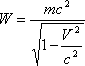. (7.4)

Дененің толық энергиясы оң шама және тыныштық күйде ол нөлге тең емес. кездегі дененің толық энергиясы тыныштық энергиясы деп аталады

. (7.5)

Бұл (7.5) формуласы дененің тыныштық энергиясы мен оның массасы арасындағы өзара байланысты орнықтырады. Кез келген денеде масса мен энергияның бір-біріне пропорционал болатындығын көрсетеді. Дененің тыныштық энергиясының әрбір өзгерісі оның массасының пропорционалдық өзгерісін тудырады.

---

Тұйықталған жүйенің толық энергиясы сақталады. Энергияның сақталу заңы - уақыттың біртектілігінің салдары.

Қозғалыс энергиясы, яғни кинетикалық энергия да - толық энергияның бір бөлігі. Сондықтан дененің кинетикалық энергиясы толық энергия мен тыныштық энергиясының айырмасы ретінде анықталады

. (7.6)

Энергия мен импульс бір-бірінен бөліп қарастырғанда салыстырмалы, яғни әртүрлі санақ жүйелерінде мәндері әртүрлі болады. Бірақ біріккен түрінде олар Лоренц түрлендіруіне қатысты инвариантты болатын бөлшек күйінің абсолютті сипатамасын береді. Осы шаманың инвариантты болуына байланысты импульс пен энергияның релятивтік өзара байланысы шығады: бір инерциалдық санақ жүйесінен екінші инерциалдық санақ жүйесіне көшкенде бөлшектің импульсы мен энергиясы біріккен түрі сақталып қалатындай болып өзгереді.

Салыстырмалық теориясының негізгі қорытындысы - кеңістік пен уақыт өзара органикалық байланыста болады да материяның өмір сүруінің бірден бір түрі - кеңістік пен уақытты құрады.

8 дәріс. Статистикалық бөлінулер

Дәрістің мақсаты:

 статистикалық және термодинамикалық зерттеу әдістерінің маңыздылығын анықтау;

 классикалық статистикалық физиканың негізгі заңдарын оқып үйрену.

8.1 Зерттеудің статистикалық және термодинамикалық тәсілдері. Ықтималдылық

Молекулалық физика және термодинамика - молекулалар мен атомдардың орасан зор жиынынан тұратын денелердегі макроскопиялық процестерді зерттейтін физиканың бөлімі.

Молекулалық физикада зерттелетін жүйелер орасан көп бөлшектерден тұратыны ескерілетін болғандықтан, оларға механикада қолданылатын зерттеу әдістері жарамайды. Механикада әрбір дененің қозғалысын сипаттау үшін әрқайсысына қозғалыс теңдеуін жазып, кез келген уақыт кезеңіне сай бөлшектің координатын табамыз. Координаттың уақыт бойынша өзгеруін біле отырып, дененің жылдамдығын, үдеуін, импульсін және т.б. физикалық шамаларын анықтауға болады. Мысалы, газдың бір моліндегі молекулалардың қозғалысын сипаттау үшін теңдеу жазылып, шығарылуы қажет. Ол мүмкін емес. Тіпті біз осындай сан теңдеулерді шығардық делік, бірақ одан тұтас жүйені (затты) сипаттайтын қасиеттер жайында мағлұматтар ала алмаймыз. Молекулалық физика зерттейтін құбылыстар орасан көп молекулалардан құралған жүйелерде (денелерде, заттарда) болып өтетіндіктен, мұндай жүйелердің ерекшелігі мұнда дара молекулаға тән емес, тек жүйені ғана тұтас сипаттайтын қасиеттер пайда болады. Мұндай қасиеттерге, мысалы, қысым және температура жатады. Қысым мен температура тек бір ғана молекулаға қатысты деп айтуға болмайды. Осындай орасан көп бөлшектерден тұратын жүйелерді зерттеу әдістері де ерекше. Олар: молекула-кинетикалық немесе статистикалық және термодинамикалық әдістер деп аталады.

Денелердің әртүрлі қасиеттерін және зат күйінің өзгерістерін зерттеумен термодинамика шұғылданады. Алайда термодинамиканың молекула-кинетикалық теориядан айырмашылығы, ол - денелер мен табиғат құбылыстарының макраскопиялық суреттемесін ескермей, тек олардың макроскопиялық қасиеттерін ғана зерттейді. Термодинамиканың негізінде көптеген тәжірибелік деректердің жинағын жалпылау арқылы тағайындалған бірнеше негізгі заңдар жатыр (оларды термодинамиканың бастамалары деп атайды). Осы себептен термодинамиканың қорытындылары өте жалпы сипатта болады.

---

Статистикалық физика макроденелердің құрылымы жөніндегі атом-молекулалық көрініс моделі (мысалы, идеал газ моделі) және математикалық статистикаға негізделген. Макрожүйелердің қасиеті жүйені құрайтын бөлшектердің қасиеті бойынша, олардың қозғалысының ерекшеліктері және осы бөлшектердің динамикалық сипаттамаларының (энергия, жылдамдық және т.б.) орташа мәндері бойынша анықталады. Статистикалық физика орташа шамаларды есептеу әдістерін және олардың көмегімен жүйенің макропараметрлерін анықтауға үлкен мүмкіндік береді. Молекула-кинетикалық теорияның негізгі теңдеуі осындай жолмен алынған

, (8.1)

мұндағы p – газдың қысымы;

n – бірлік көлемдегі газ молекулаларының саны (молекула концентрациясы);

– молекулалардың ілгерілемелі қозғалысының орташа кинетикалық энергиясы.

Бұл теңдеу бойынша қысым бірлік көлемдегі молекулалардың ілгерлемелі қозғалысының кинетикалық энергиясының үштен екісіне тең болады.

Зат күйінің өзгерістерін әр түрлі көзқарас тұрғысында қарастыра отырып, термодинамика мен молекула-кинетикалық теория бір-бірін толықтырып, негізінен біртұтас ілім құрайды.

8.2 Максвелл бөлінуі

Газ молекулалары ретсіз, хаосты қозғалады. Қозғалыс бағытының ықтималдылығы бірдей, олардың қайсысының да басқаларынан ешбір артықшылығы жоқ. Сондықтан, молекулалардың бағыттары бойынша таралуы бір қалыпты болады.

Молекулалардың жылдамдықтарының шамалары әртүрлі бола алады. Нөлден шексіздікке дейінгі аралықтағы жылдамдықтың мүмкін мәндерін бірдей ықтималды дей алмаймыз. Молекулалардың жылдамдығының соқтығысу кезінде өзгеруі кездейсоқ өтеді. Қайсыбір жеке молекула бірқатар жүйелі соқтығысқан сайын өз сыңарларынан энергия алып отыруы мүмкін, соның нәтижесінде оның энергиясы ε орташа мәнінен артып кетеді. Алайда газдың барлық молекулалары өз энергияларын жалғыз молекулаға беріп, өздері тоқталып қалады деп ойлағанның өзінде бұл молекуланың энергиясы, демек, оның жылдамдығы, шектеулі шамада болады. Сөйтіп, газ молекулаларының жылдамдығы қандай да бір -нан басталып ∞-пен бітетін мәндер қабылдай алмайды. Барлық молекулалардың қорытқы энергиясының едәуір үлесін бір молекулаға беретін процестер ықтималдылығы өте аз болады деп есептей отырып, мәні жылдамдықтың орташа мәнінен әлдеқайда артық жылдамдықтар да өте сирек кездеседі деген тұжырымға келеміз. Дәл осы тәрізді, соқтығысулар кезінде молекуланың жылдамдығы нөлге айналады деп те айтуға болмайды. Демек, жылдамдықтың орташа мәнімен салыстырғанда өте аз және өте үлкен жылдамдықтардың пайда болуының да ықтималдылығы өте аз болады, сонымен қатар -нің осы мәнінің ықтималдылығы →0 кезінде де, →∞ кезінде де нөлге ұмтылады. Осы айтылғандардан, молекулалардың жылдамдықтары жылдамдықтың аса ықтимал мәнінің төңірегінде топтасатындығы шығады.

---

Смотрите также файлы

• Физика дәріс.docx

• Философия методичка рус.doc

• Философия.docx

• Электротехникалық материалтану зертаханалық жұмыс 3,4.docx

• Электростатика.doc