ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 24
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вопрос 17. Статистика основных фондов
Основные фонды (основные средства, основной капитал) – это произведенные активы, подлежащие использованию неоднократно или постоянно в течение длительного периода времени (не менее одного года) для производства товаров или оказания рыночных и нерыночных услуг.
Для изучения состава основных фондов используются группировки по следующим признакам: 1) по отраслям экономики; 2) по формам собственности; 3) по степени участия в производственном процессе; 4) по принадлежности; 5) по территориальному размещению – основные фонды районов, республик, областей, городов.
В настоящее время в статистике РФ действует следующая типовая классификация основных фондов: 1) здания (кроме жилья); 2) сооружения; 3) жилые здания; 4) машины и оборудование; 5) транспортные средства; 6) производственный и хозяйственный инвентарь; 7) рабочий скот; 8) продуктивный скот; 9) многолетние насаждения; 10) прочие виды основных фондов.
Нематериальные основные фонды (нематериальные произведенные активы) классифицируются следующим образом:
1) расходы на разведку полезных ископаемых;
2) компьютерное программное обеспечение и базы данных;
3) оригинальные произведения развлекательного жанра, литературы и искусства;
4) наукоемкие промышленные технологии.
Основные фонды могут быть учтены в натуральных и стоимостных единицах измерения.
Натуральные единицы измерения стоимости основных фондов используются для измерения объема определенного вида основных фондов.
Существуют следующие виды стоимостной оценки основных фондов:
1) полная первоначальная стоимость – это стоимость объекта на момент ввода его в эксплуатацию.
2) остаточная первоначальная стоимость – это полная первоначальная стоимость за вычетом суммы износа основных фондов за время их эксплуатации.
3) полная восстановительная стоимость – это стоимость воспроизводства основных фондов в современных условиях, т. е. стоимость приобретения, транспортировки, установки или сооружения аналогичных новых, неизношенных объектов на момент переоценки.
4) остаточная восстановительная стоимость – это полная восстановительная стоимость основных фондов за вычетом суммы износа.
5) балансовая стоимость – это стоимость объектов с учетом переоценки, по которой они числятся на балансе предприятия.
Основные средства в процессе эксплуатации подвергаются физическому и моральному износу. Физический износ — это утрата основными фондами своих физических свойств (в результате чего они не могут выполнять свои функции и приходят в негодность). Моральный износ проявляется в том, что действующие объекты основных фондов по своей производительности, расходам на обслуживание, качеству выпускаемой продукции начинают уступать новым образцам основных фондов, т.е. становятся экономически невыгодными.
Вследствие физического и морального износа периодически возникает необходимость замены основных фондов. Для этого в течение срока полезного использования объектов основных фондов затраты предприятия, связанные с их приобретением или созданием, должны быть возмещены и накоплены денежные средства, достаточные для осуществления замены. Возмещение затрат и накопление денежных средств достигается путем включения в себестоимость продукции части стоимости действующих основных фондов в виде амортизационных отчислений.
Вопрос 22. Методы изучения дифференциации доходов населения, уровня и границ бедности
К числу важнейших методов изучения дифференциации доходов населения относится построение вариационных рядов, и на их основе, - статистических рядов распределения населения по уровню среднедушевых денежных доходов, представляющих собой ранжированные и сгруппированные в определенных интервалах по величине дохода результаты наблюдения.
Для характеристики дифференциации доходов населения и уровня бедности рассчитываются следующие показатели:
1. Модальный доход – уровень дохода наиболее часто встречающихся среди населения;
2. Медианный доход – показатель дохода, находящегося в середине ранжированного ряда распределения. Половина населения имеет доход ниже медианного, а вторая половина – выше;
3. Средний доход – общий средний уровень дохода всего населения;
При статическом изучении уровня и границ бедности, прежде всего, устанавливается граница дохода, обеспечивающая потребление на минимально допустимом уровне, т.е. определяется стоимостная величина прожиточного минимума, с которой сравниваются фактические доходы отдельных слоев населения.
Прожиточный (физиологический) минимум – суммарная стоимость товаров и услуг, которую можно рассматривать как нижний предел, позволяющий поддержать физическое состояние, но лишь в течение определенного времени. Жизненно необходимый уровень потребления включает только расходы на питание, самые необходимые предметы санитарии и гигиены, лекарства, коммуникальные услуги и другие обязательные платежи.
Бедность является одной из важнейших характеристик неравенства в распределении доходов. Уровень бедности – удельный вес населения с доходами ниже прожиточного минимума в общей численности населения выступает информативным показателем социально-экономического положения страны. Обычно бедность определяется как состояние, когда экономических ресурсов не хватает для обеспечения прожиточного минимума.
На основе данных о доходах бедного населения рассчитываются относительно новые для социальной статистики показатели:
1. Дефицит дохода оценивается как суммарный доход малоимущего недостающий до величины прожиточного минимума.
2. Коэффициент глубины бедности характеризует дефицит дохода обследуемых домохозяйств в виде среднего простого отклонения их доходов от прожиточного минимума в расчете на одно домохозяйство.
3. Коэффициент остроты бедности также отражает дефицит дохода обследуемых домохозяйств, но рассчитывается по средневзвешенному отклонению их доходов от прожиточного минимума (т.е. придается больший вес домохозяйствам с более высоким дефицитом дохода).
Вопрос 27. Статистические методы оценки структуры бюджета
Статистические методы и приемы позволяют проводить исследования структуры бюджетов в условиях определенного места и времени, поэтому большое практическое значение имеет исследование структуры бюджетов любых уровней в динамике, оценка структурных сдвигов, выявление и характеристика основных тенденций бюджетной политики.
Для характеристики изменения структуры или структурных сдвигов применяют две группы показателей:
- показатели, которые базируются на разнице между удельными весами одноименных частей совокупности,
- показатели, которые базируются на динамическом усреднении удельных весов частей совокупности.
Для анализа изменения структуры за определенный временной
интервал используют различные обобщающие показатели структурных сдвигов.
Линейный коэффициент абсолютных структурных сдвигов:
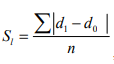 , где
, гдеи – удельные веса, в % отдельных структурных элементов в рассматриваемом и предыдущем периодах, n – число выделяемых структурных элементов. Этот показатель отражает среднее изменение удельного веса (в процентных пунктах) за рассматриваемый временной интервал в целом по всем структурным частям.
Линейный коэффициент абсолютных структурных сдвигов является средним арифметическим абсолютных приростов удельного веса всех частей явления. Он показывает, на сколько процентных пунктов в среднем отклоняется одна от другой удельный вес всех частей изучаемого явления за исследуемый период.
Чтобы избежать взаимопогашения разных по знаку изменений долей, вместо модулей применяют квадраты отклонений и получают квадратический коэффициент абсолютных структурных сдвигов:
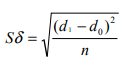
Использование квадратического коэффициента предпочтительнее, так как он более чутко реагирует на колебания структуры.
При отсутствии сдвигов в структуре эти показатели равны нулю. Верхней границы изменения коэффициенты не имеют: чем больше изменения структуры, тем выше значения коэффициентов. В отличие от них индекс различий имеет не только нижнюю, но и верхнюю границу изменения.
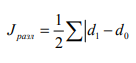 , где
, гдеd1 и d0 – показатели удельного веса, выраженные в долях.
0 ‹ J разл‹ 1
Чем ближе значения индекса различий к 1, тем более значительны изменения структуры.
Линейный и квадратичный коэффициенты позволяют получить сводную оценку скорости изменения удельных весов отдельных частей совокупности и сравнить общую динамику структурных сдвигов. Квадратический коэффициент абсолютных структурных сдвигов, как и линейный коэффициент абсолютных структурных сдвигов показывает, на сколько процентных пунктов в среднем отклоняется одна от другой удельный вес всех частей изучаемого явления за исследуемый период.
Обобщающим показателем интенсивности структурных сдвигов, который дает возможность количественно оценить размеры структурных изменений, является интегральный коэффициент структурных сдвигов:
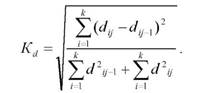
Интегральный коэффициент структурных сдвигов изменяется от 0 до 1,00 или от 0 до 100%. Чем меньше разница между сравниваемыми структурами, тем коэффициент будет ближе к 0,01 или 1,00 и наоборот, чем более крупные структурные сдвиги, тем он будет ближе к 1,00 или 100%.
Вопрос 32. Оценка параметров регрессионного уравнения. Метод наименьших квадратов, его оценка. Метод постановки. Оценка наименьших квадратов. Условие идентифируемости модели наблюдений. Матричная модель парной регрессии. Решение системы нормальных уравнений в матричной форме.
Для оценки параметров регрессионного уравнения наиболее часто используют метод наименьших квадратов.
Метод наименьших квадратов (МНК) дает оценки, имеющие наименьшую дисперсию в классе всех линейных оценок, если выполняются предпосылки нормальной линейной регрессионной модели. МНК минимизирует сумму квадратов отклонения наблюдаемых значений yi от модельных значений j>,.
Оценки a, Р находят путем минимизации суммы квадратов
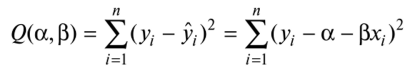
по всем возможным значениям а и (3 при заданных (наблюдаемых) значениях х,, хп, у{, уп. Задача сводится к математической задаче поиска точки минимума функции двух переменных. Точка минимума находится путем приравнивания к нулю частных производных функции z = Q(ос, Р) по переменным а и р. Это приводит к системе нормальных уравнений
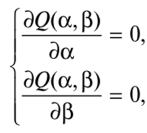
решением которой и является пара а, р.
Согласно правилам вычисления производных имеем
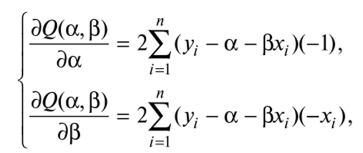
так что искомые значения d, Р удовлетворяют соотношениям
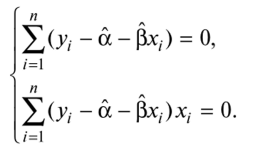
Эту систему двух уравнений можно записать также
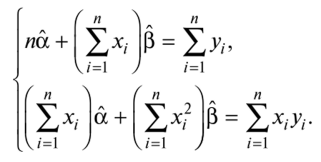
Она является системой двух линейных уравнений с двумя неизвестными и может быть легко решена, например, методом подстановки. В результате получаем так называемые оценки наименьших квадратов: