ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 25
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
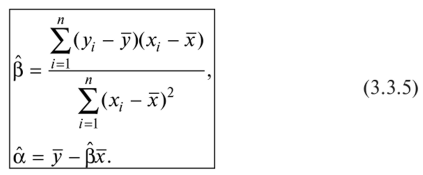
Такое решение может существовать только при выполнении условия
что равносильно отличию от нуля определителя системы нормальных уравнений. Действительно, этот определитель равен
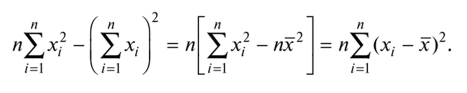
Условие (3.3.6) называется условием идентифицируемости модели наблюдений yt = (а + (Ц) + е;., i = 1, п, и означает, что не все значения х{, ...,хп совпадают между собой. При нарушении этого условия все точки (х., у{), i = 1, п, лежат на одной вертикальной прямой х = х.
Обратим внимание на полученное выражение для параметра (3 [см. формулу (3.3.5)]. Сюда входят выражения, участвовавшие ранее в определении выборочной дисперсии
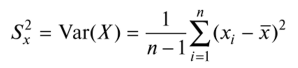
и выборочной ковариации,
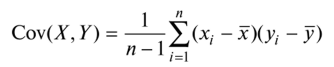
так что в этих терминах параметр р можно получить следующим образом:
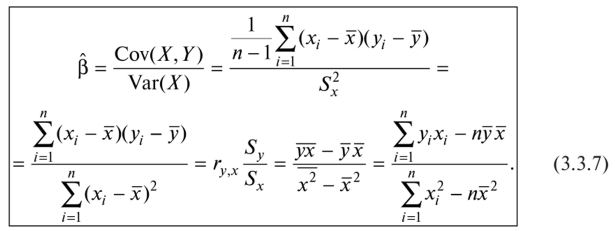
В матричной форме модель парной регрессии имеет вид
где Y — вектор-столбец размерности п х 1 наблюдаемых значений зависимой переменной; X — матрица размерности пх2 наблюдаемых значений факторных признаков (дополнительный фактор х0, состоящий из одних единиц, вводится для вычисления свободного члена); а — вектор-столбец размерности 2 х 1 неизвестных, подлежащих оценке коэффициентов регрессии; ? — вектор-столбец размерности п х 1 ошибок наблюдений.
Таким образом,
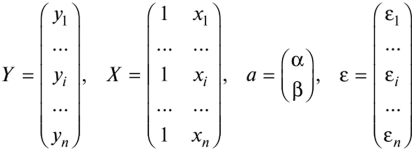
Решение системы нормальных уравнений в матричной форме имеет вид
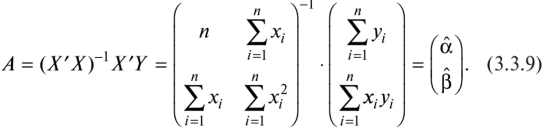
Вопрос 37. Оценка значимости уравнений регрессии с помощью критерия Фишера. Оценка коэффициента уравнения регрессии с мощью критерия Стьюдента. Признание значимым уравнения регрессии. Составление краткосрочных прогнозов.
Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. Согласно F-критерию Фишера, выдвигается «нулевая» гипотеза H0 о статистической незначимости уравнения регрессии и показателя тесноты связи.
Непосредственному расчету F-критерия предшествует анализ дисперсии.
Наблюдаемые значения результативного признака yi можно представить в виде суммы двух составляющих ŷi и εi:
yi = ŷi+ εi
Из данного уравнения следует следующее соотношение между дисперсиями наблюдаемых значений переменной D(y), ее расчетных значений D(ŷ) и остатков D(е) (остаточной дисперсией Dост = D(ε)):
D(y) = D(ŷ) + D(ε)
| полная (общая) сумма квадратов отклонений | = | сумма квадратов отклонений, объясненная регрессией | + | (остаточная) сумма квадратов отклонений, не объясненная регрессией |
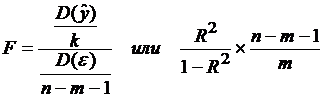
где m – число независимых переменных в уравнении регрессии (для парной регрессии m = 1);
n– число единиц совокупности.
Если нулевая гипотезаН0 справедлива, то факторная и остаточная дисперсии не отличаются друг от друга (т. е. отличие величины F от нуля статистически незначимо).
Если нулевая гипотеза Н0не справедлива, то факторная дисперсия превышает остаточную в несколько раз.
Уровнем значимости (обозначается α) в статистических гипотезах называется вероятность отвергнуть верную гипотезу (это, так называемая, ошибка первого рода). Уровень значимости α обычно принимает значения 0,05 и 0,01, что соответствует вероятности совершения ошибки первого рода 5 % и 1 %.
Число степеней свободы связано с числом единиц совокупности n и с числом определяемых по ней констант. В таблице значений F-критерия Фишера число степеней свободы k1 = m, k2 = n -m-1.
Табличное значение F-критерия – это максимальная величина отношения дисперсий, которая может иметь место при случайном расхождении их для данного уровня вероятности наличия нулевой гипотезы.
Если Fфакт >Fтабл, то Н0 о случайной природе связи отклоняется и признается статистическая значимость и надежность уравнения.
Если Fфакт
Для оценки статистической значимости коэффициентов регрессии применяется t-критерий Стьюдента, согласно которому выдвигается «нулевая» гипотеза H0 о статистической незначимости коэффициента уравнения регрессии (т. е. о статистически незначимом отличии величины а или b от нуля):
Н0: а=0, b=0
Эта гипотеза отвергается при выполнении условия t > tтабл, где tтабл определяется по таблицам t-критерия Стьюдента по числу степеней свободы k1 = n-m-1 (m - число независимых переменных в уравнении регрессии) и заданному уровню значимости α.
t-критерий Стьюдента используется и для оценки статистической значимости выборочного коэффициента корреляции rxy:
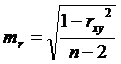
Оценка значимости параметров уравнения и коэффициента корреляции проводится путем сопоставления их значений с величиной случайной ошибки:
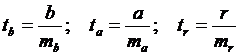
Если tфакт >tтабл, то Н0 отклоняется, т.е. a, b, r не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х.
Если tфакт
Прогнозируемое значение переменной У получается при подстановке в уравнение регрессии ожидаемой величины фактора Х:
Следует соблюдать одно ограничение: нельзя подставлять значения факторного признака, значительно отличающиеся от входящих в базисную информацию, по которой вычислено уравнение регрессии.
Прогноз, полученный подстановкой в уравнение регрессии ожидаемого значения фактора, называют точечным прогнозом. Вероятность точной реализации такого прогноза крайне мала. Необходимо сопроводить его расчетом значения средней ошибки прогноза или доверительного интервала прогноза с достаточно большой вероятностью (надежностью).
Доверительные интервалы зависят от следующих параметров:
– стандартная ошибка
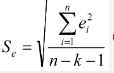
– отклонение хпрогн от своего среднего значения
– количество наблюдений n;
– уровень значимости прогноза α.
В частности для прогноза будущие значения упрогн с вероятностью
(1 – α) попадут в доверительный интервал:
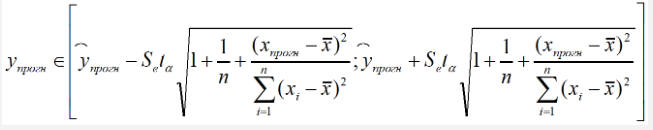
Расположение границ доверительного интервала показывает, что прогноз значений зависимой переменной по уравнению регрессии хорош только в случае, если значение фактора Х не выходит за пределы выборки. Иными словами, экстраполяция по уравнению регрессии может привести к значительным погрешностям.