Файл: Контрольная работа за 2 семестр По дисциплине Математика Вариант 2 Фамилия Имя.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 28
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ им. проф. М.А. Бонч-Бруевича
ФАКУЛЬТЕТ ВЕЧЕРНЕГО И ЗАОЧНОГО ОБУЧЕНИЯ
Контрольная работа за _2_ семестр
По дисциплине _Математика_
Вариант _2_
Фамилия:__ __
Имя:___ ____
Отчество:_ _
Курс:____________
Студ. билет № :___ ___
Группа №:___ ___
Дата сдачи работы:______________
Санкт-Петербург
2022_
_Дисциплина_Математика , Назаров_, _ПБ-12з_
| Рецензия 1 | Дата получения работы:_____________ | Рецензия 2 | Дата получения работы:_____________ | ||
| №_________________________________________ ___________________________________________ | №_________________________________________ ___________________________________________ | ||||
| №_________________________________________ ___________________________________________ | №_________________________________________ ___________________________________________ | ||||
| №_________________________________________ ___________________________________________ | №_________________________________________ ___________________________________________ | ||||
| №_________________________________________ ___________________________________________ | №_________________________________________ ___________________________________________ | ||||
| №_________________________________________ ___________________________________________ | №_________________________________________ ___________________________________________ | ||||
| №_________________________________________ ___________________________________________ | №_________________________________________ ___________________________________________ | ||||
| №_________________________________________ ___________________________________________ | №_________________________________________ ___________________________________________ | ||||
| №_________________________________________ ___________________________________________ | №_________________________________________ ___________________________________________ | ||||
| №_________________________________________ ___________________________________________ | №_________________________________________ ___________________________________________ | ||||
| Оценка:_____________ | Баллы:_____________ | Оценка:_____________ | Баллы:_____________ | ||
| Дата: __________________ | Подпись преподавателя: _______________________ | Дата: ________________ | Подпись преподавателя: _______________________ | ||
| | | ||||
| Рецензия 3 | Дата получения работы:_____________ | Рецензия 4 | Дата получения работы:_____________ | ||
| №_________________________________________ ___________________________________________ | №_________________________________________ ___________________________________________ | ||||
| №_________________________________________ ___________________________________________ | №_________________________________________ ___________________________________________ | ||||
| №_________________________________________ ___________________________________________ | №_________________________________________ ___________________________________________ | ||||
| №_________________________________________ ___________________________________________ | №_________________________________________ ___________________________________________ | ||||
| Оценка:_____________ | Баллы:_____________ | Оценка:_____________ | Баллы:_____________ | ||
| Дата: __________________ | Подпись преподавателя: _______________________ | Дата: ________________ | Подпись преподавателя: _______________________ | ||
Задача 2. Проверить потенциальность плоского поля и вычислить работу силы при перемещении материальной точки единичной массы из точки
в точку 
.
, 
, 
.Решение.
Если
- потенциальное плоское векторное поле, где 
и 
имеют непрерывные первые частные производные в некоторой области 
, то в 
справедливо тожество 
. Так как
и 
. Вычислим частные производные 
и 
. Частная производная функции 
по переменной 
, тогда 
, получим 
. Частная производная функции 
по переменной 
, тогда 
, получим 
.Тогда имеем
, следовательно, поле
потенциальное.Работа силы
при перемещении из точки 
в точку 
равна:
,так как подынтегральное выражение есть полный дифференциал функции двух переменных, то криволинейный интеграл не зависит от линии интегрирования, соединяющей точки
и . Вычислим работу по прямолинейному отрезку 
. Уравнение прямой : 
, 
, 
, где 
тогда 
.Тогда работа силы равна
.Ответ:
- потенциально и 
.Задача 12. Вычислить криволинейный интеграл:
1) по замкнутому контуру в положительном направлении (против часовой стрелки);
2
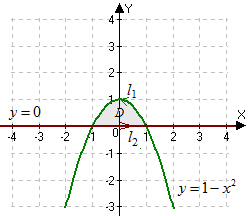) используя формулу Грина.
, 
: 
,
.Решение.
Построим контур, образованный данными линиями.
1) Введем следующую параметризацию на кривой
. На кривой 
: 
, на отрезке 
: 
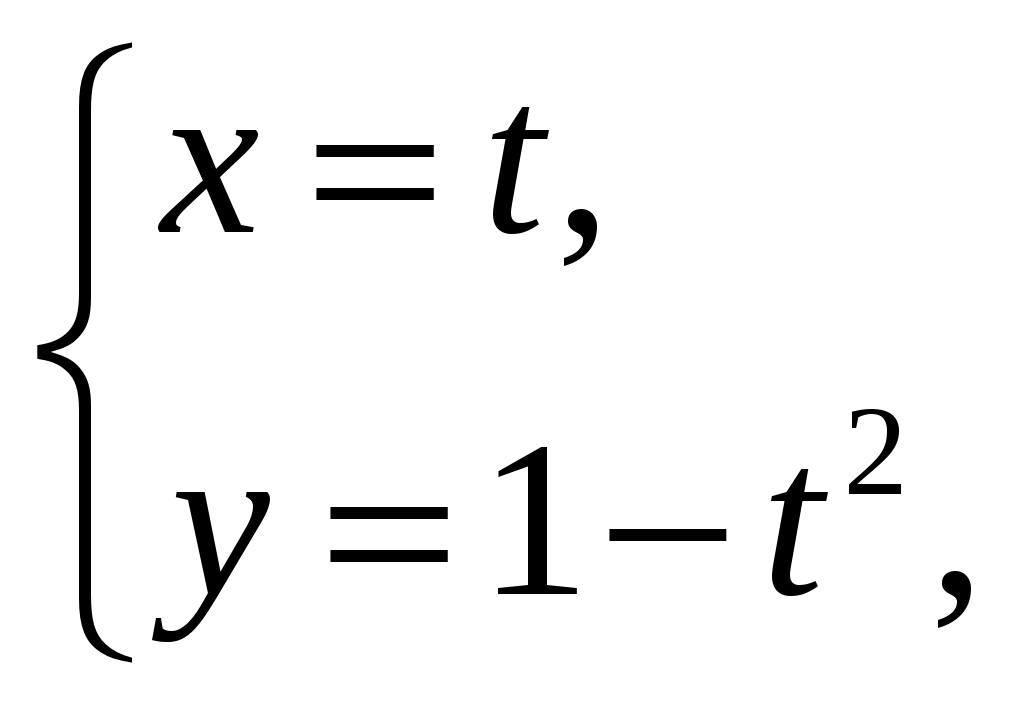
.Тогда криволинейный интеграл по контуру
можно представить в виде суммы двух интегралов, т.е. 
.Вычислим сначала каждый из интегралов:
а)
.Для кривой
: имеем 
и 
. Криволинейный интеграл равен: 
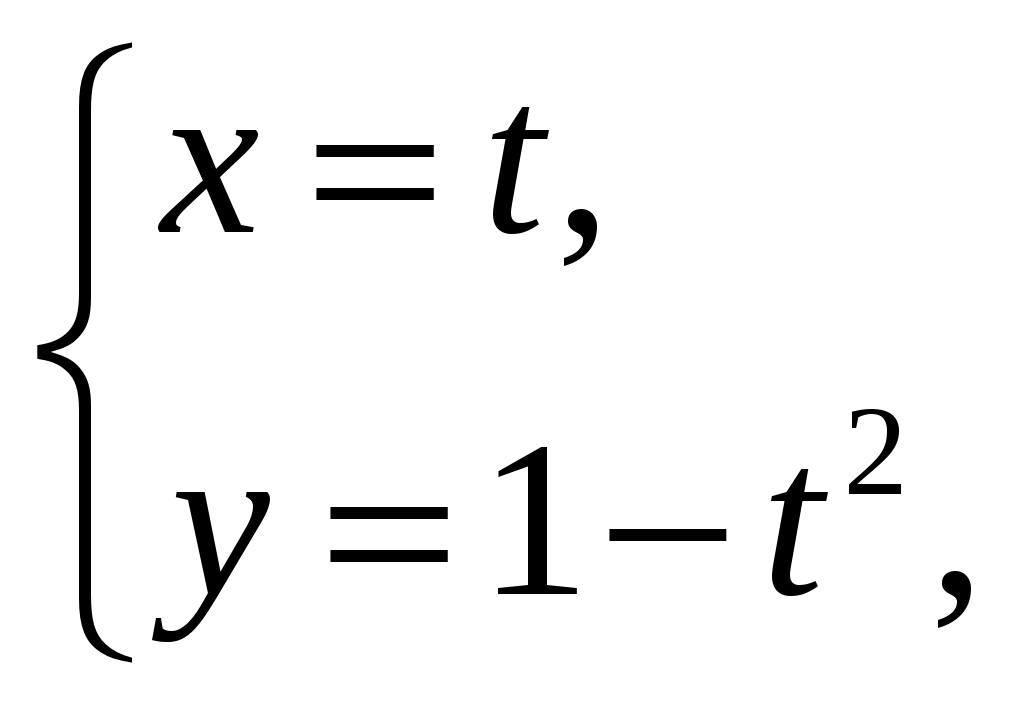
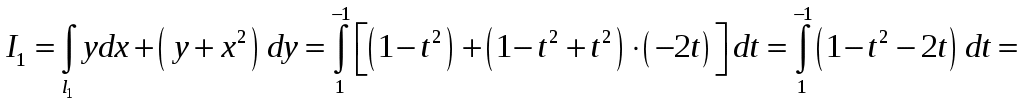
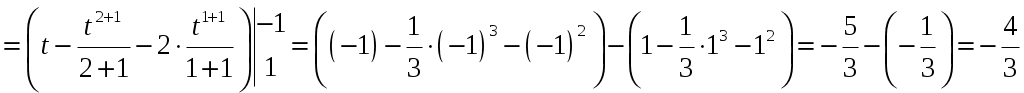.б)
.Для кривой
: имеем и 
. Криволинейный интеграл равен:
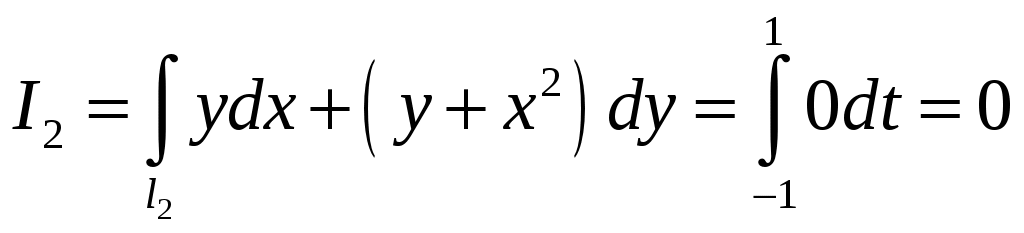.Тогда исходный интеграл равен:
.2) Для вычисления криволинейного интеграла по замкнутому контуру
используем формулу Грина 
.Так как
и 
. Вычислим частные производные 
и 
, получим: 
и 
.Тогда криволинейный интеграл равен:
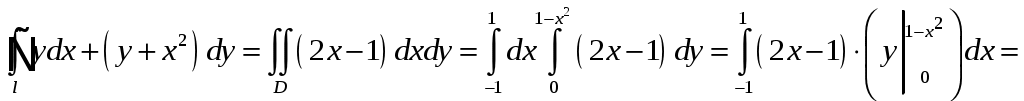
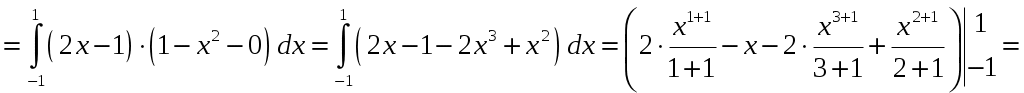
.Ответ:
.Задача 22. Найти общее решение для ДУ с разделяющимися переменными.
.Решение.
Разделим переменные
, 
. Интегрируем левую и правую части 
, получим общее решение 
.Ответ:
.Задача 32. Решить задачу Коши для линейного уравнения.
, 