Файл: Контрольная работа за 2 семестр По дисциплине Математика Вариант 2 Фамилия Имя.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 29
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Продифференцируем по обе части равенства
обе части равенства 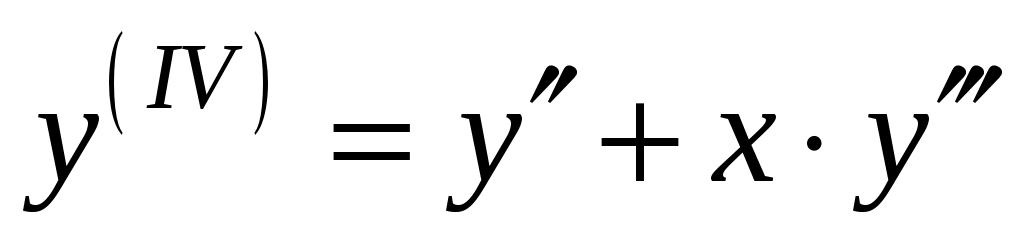 , получим:
, получим: 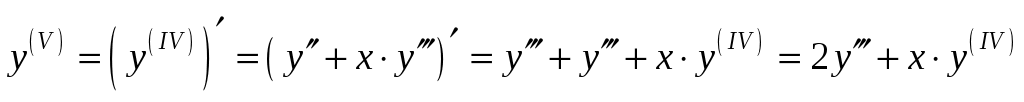 . Подставляя в него
. Подставляя в него  , получаем
, получаем 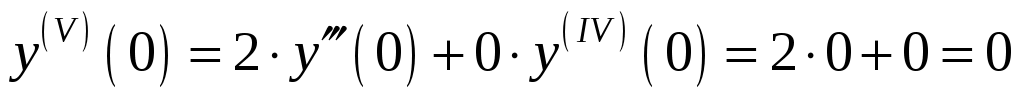 .
.
Продифференцируем по обе части равенства
обе части равенства 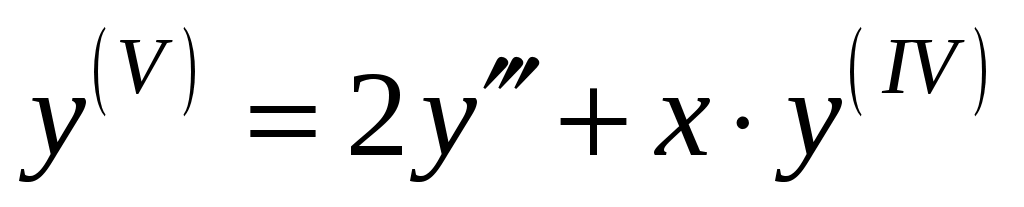 , получим:
, получим: 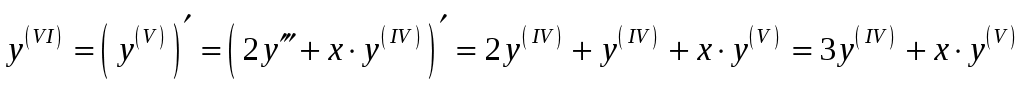 . Подставляя в него
. Подставляя в него  , получаем
, получаем 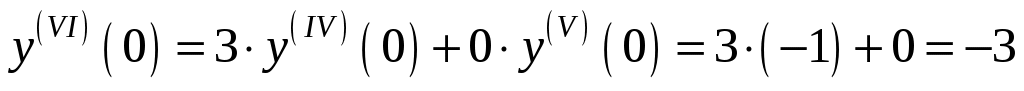 .
.
Отсюда получим ряд:
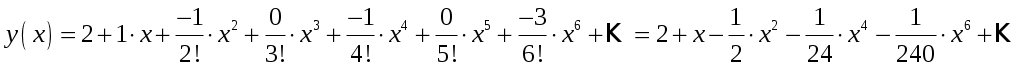
Ответ: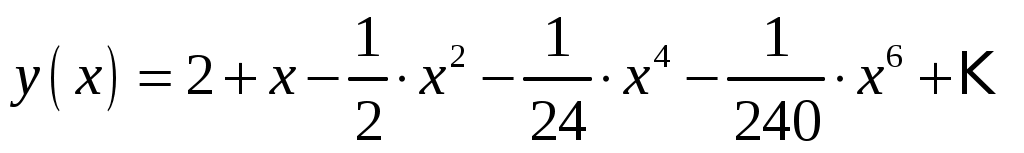 .
.
Задача 82. 1) разложить функцию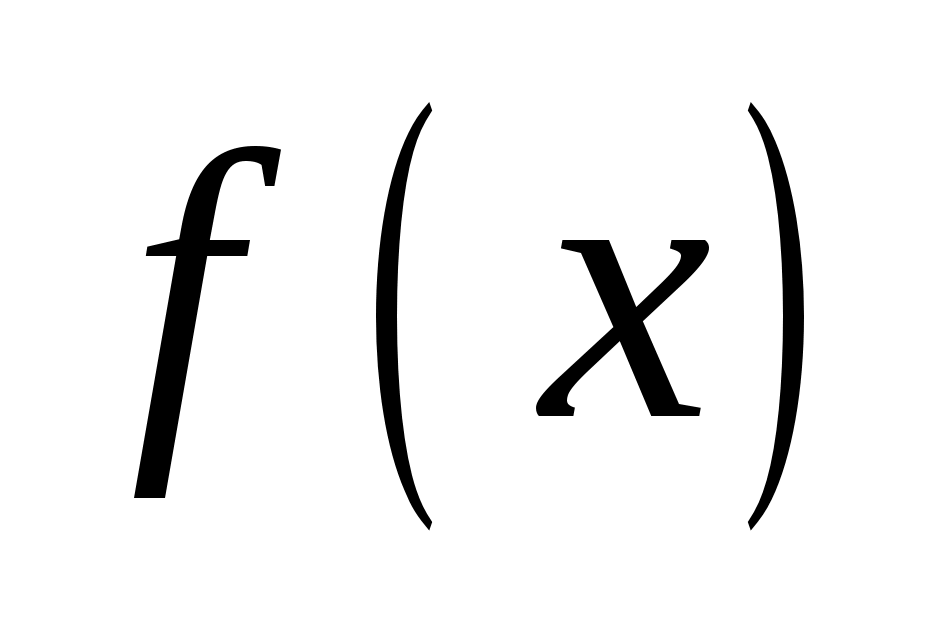 в ряд Фурье с периодом, равным длине интервала задания функции. 2) изобразить график суммы ряда
в ряд Фурье с периодом, равным длине интервала задания функции. 2) изобразить график суммы ряда 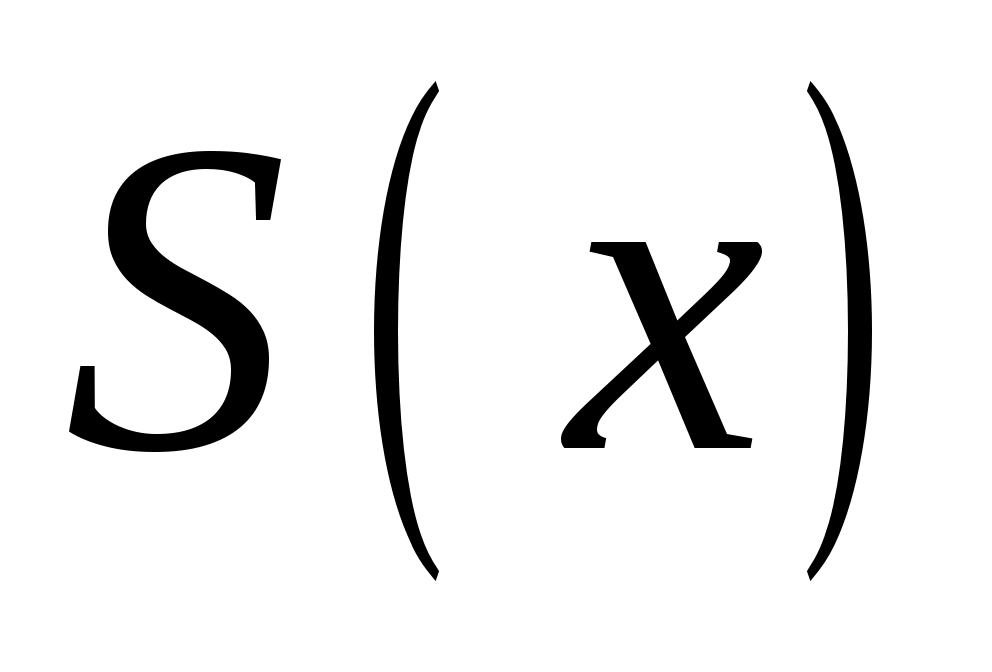 . 3) спектр амплитуд при помощи диаграмм:
. 3) спектр амплитуд при помощи диаграмм:
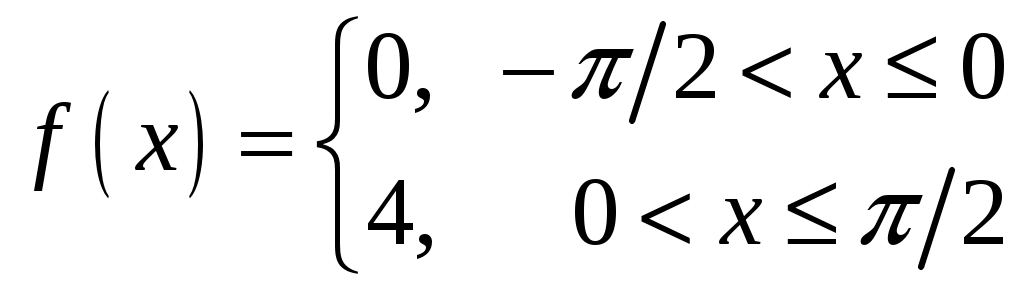
Решение.
1) Рядом Фурье функции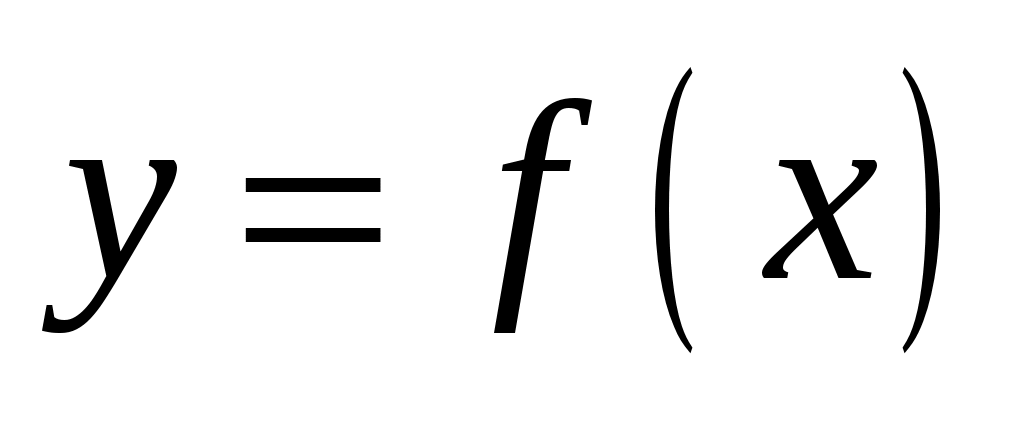 на промежутке
на промежутке 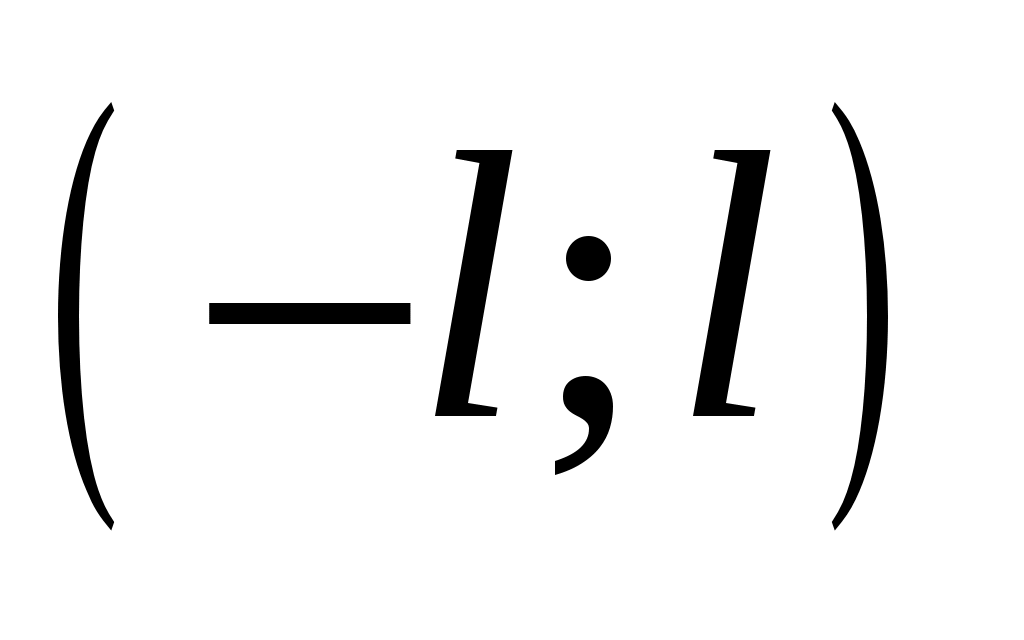 называется тригонометрический ряд
называется тригонометрический ряд 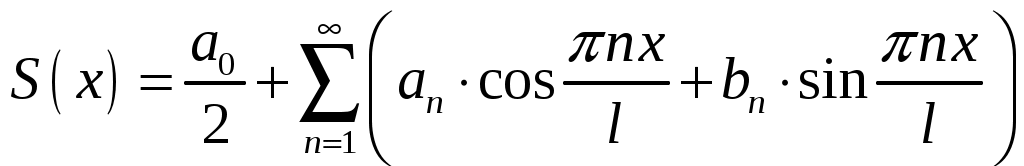 , коэффициенты которого определяются по функции
, коэффициенты которого определяются по функции 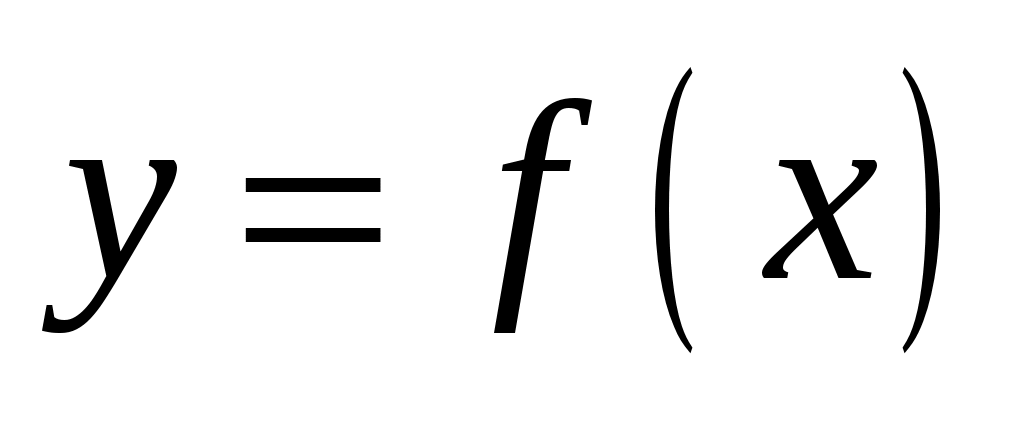 при помощи формул Фурье:
при помощи формул Фурье: 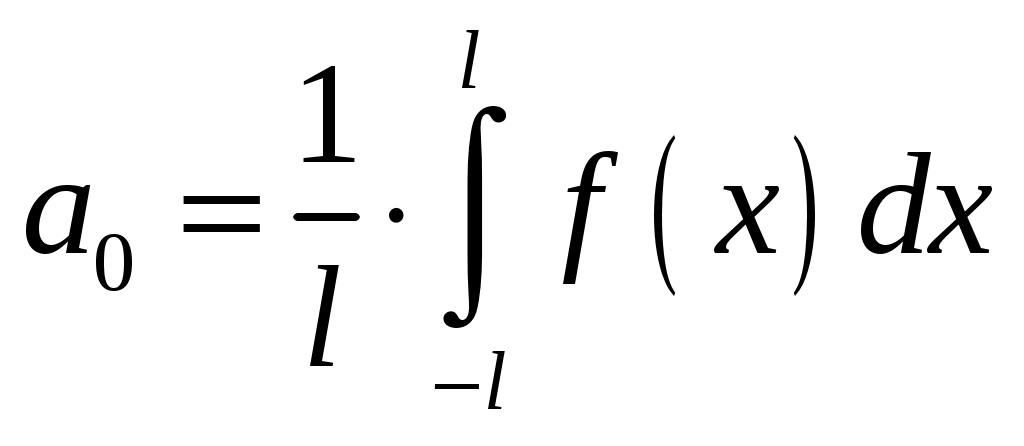 ,
, 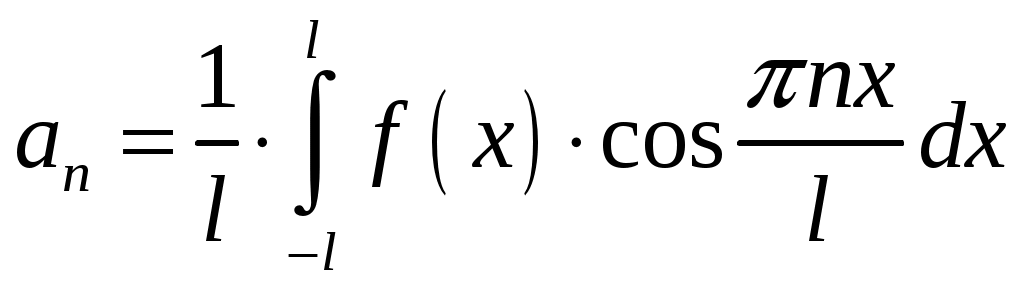 и
и 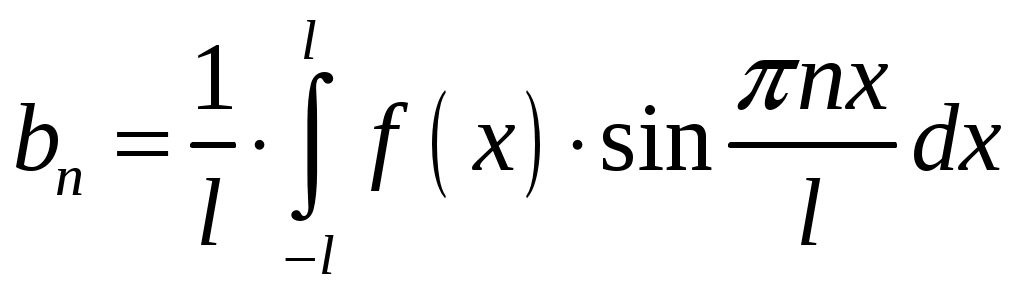 .
.
Найдем коэффициенты ряда Фурье:
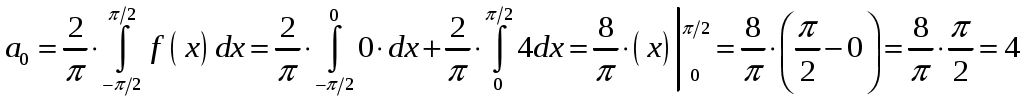 ;
;
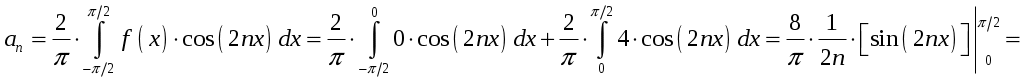
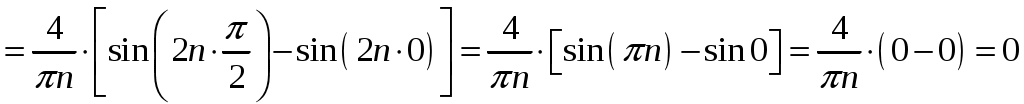 ;
;
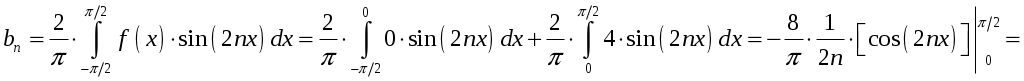
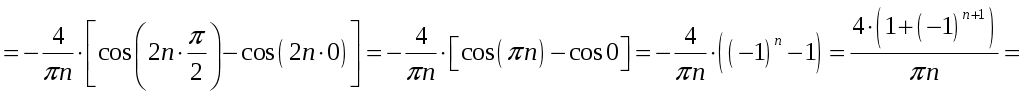
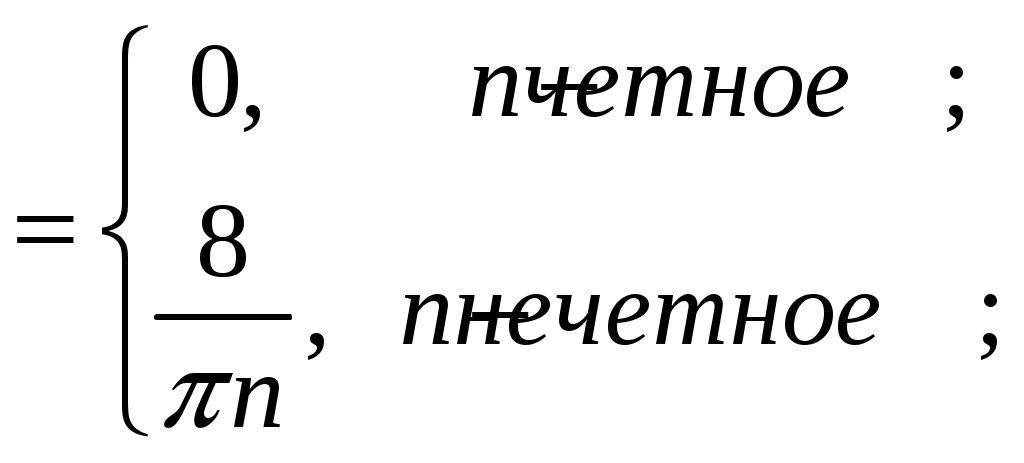 .
.
Таким образом, для функции ряд Фурье равен:
ряд Фурье равен:
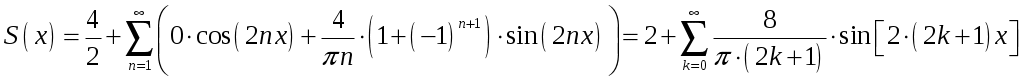 .
.
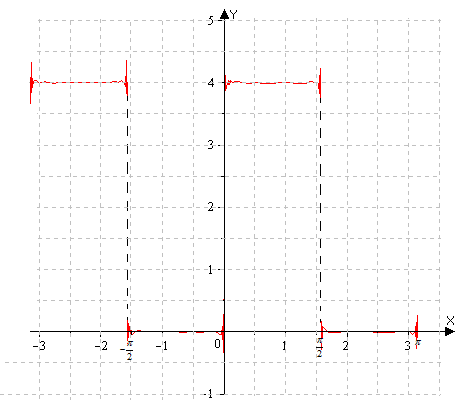
2) В соответствии с теоремой Дирихле, график суммы ряда Фурье функции имеет вид:
имеет вид:
3) Амплитуду ряда определяется по формуле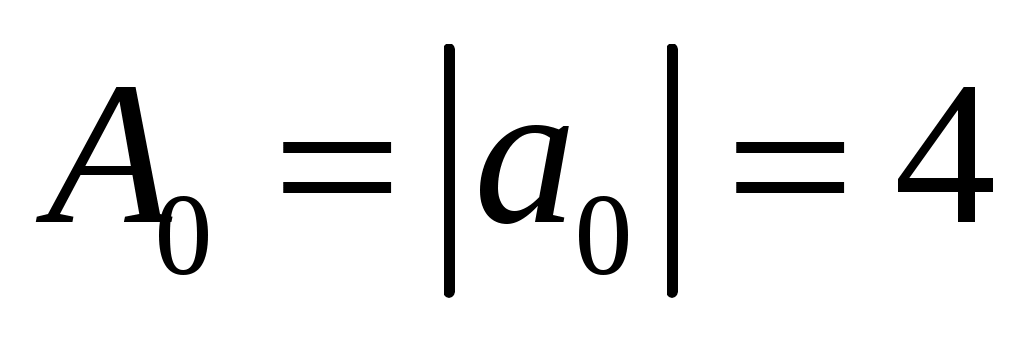 и
и 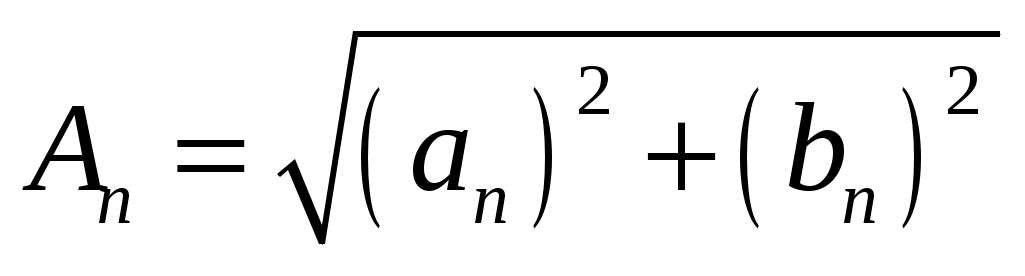 , тогда для исходного ряда амплитуда равна:
, тогда для исходного ряда амплитуда равна:
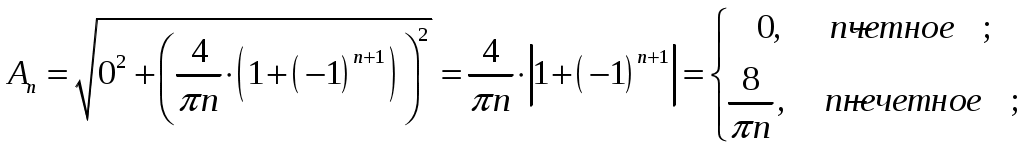 .
.
Вычислим значения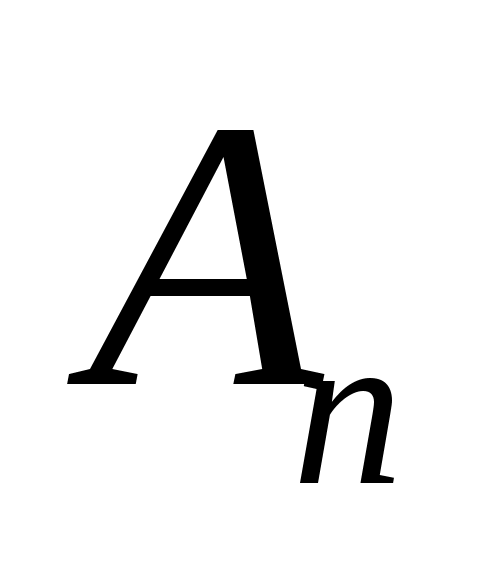 при
при  , получим:
, получим:
при , имеем
, имеем 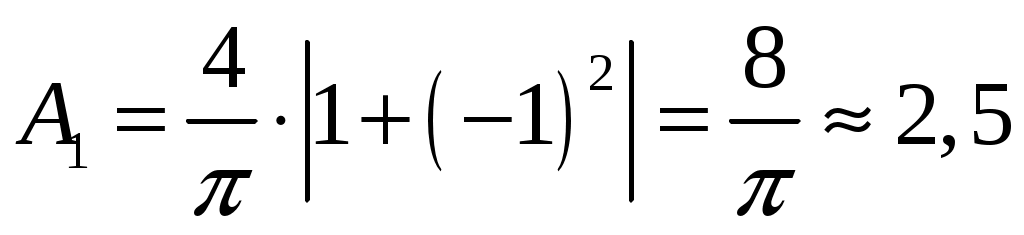 ;
;
при , имеем
, имеем 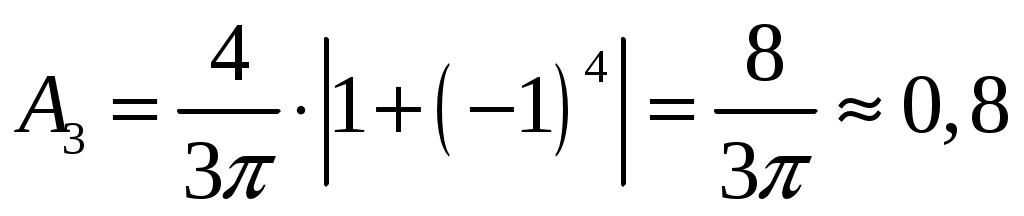 ;
;
при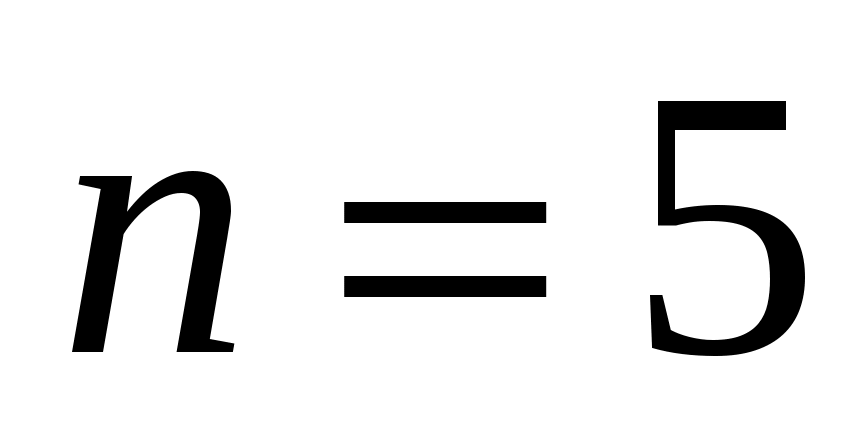 , имеем
, имеем 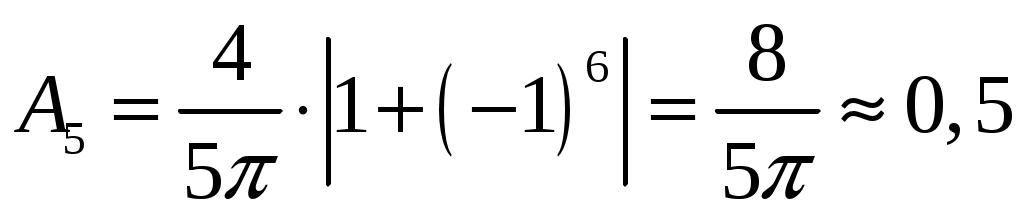 ;
;
при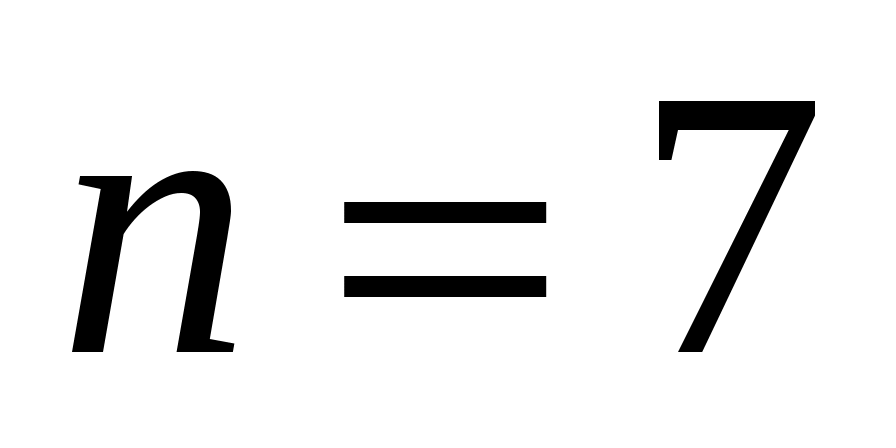 , имеем
, имеем 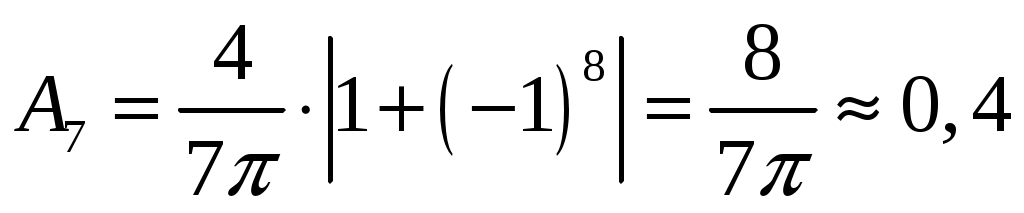 ;
;
при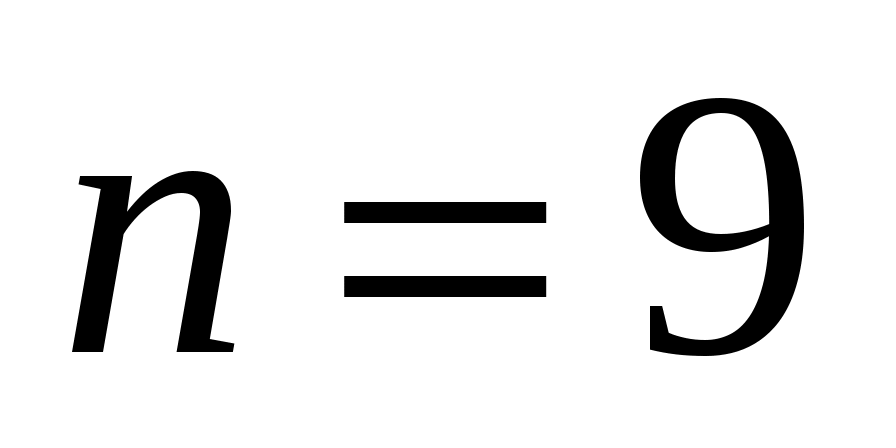 , имеем
, имеем 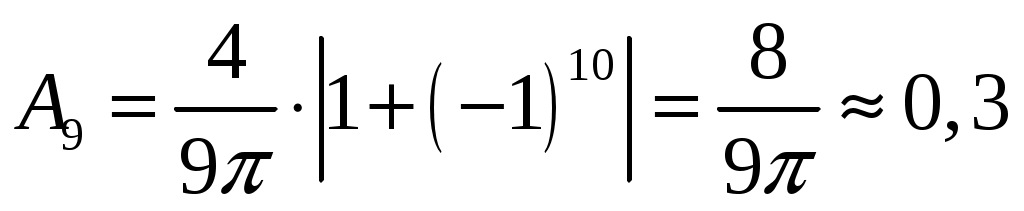
.
Изображая амплитуды на диаграмме, получаем следующую картинку:
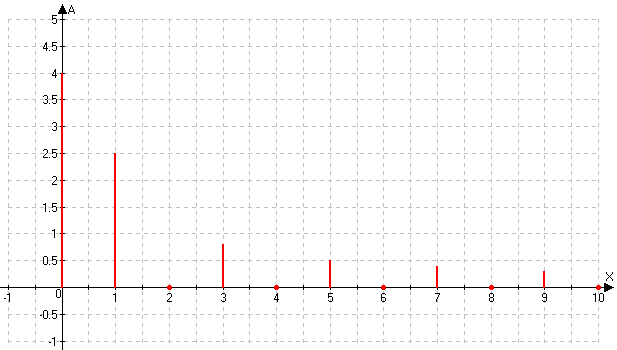
Продифференцируем по
Продифференцируем по
Отсюда получим ряд:
Ответ:
Задача 82. 1) разложить функцию
Решение.
1) Рядом Фурье функции
Найдем коэффициенты ряда Фурье:
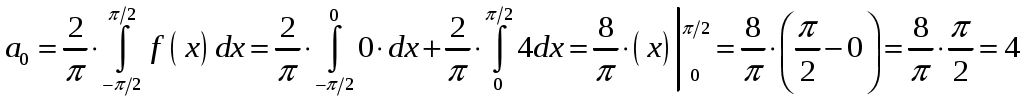 ;
;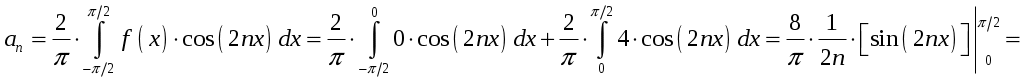
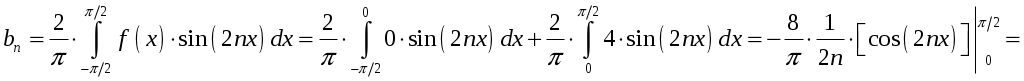
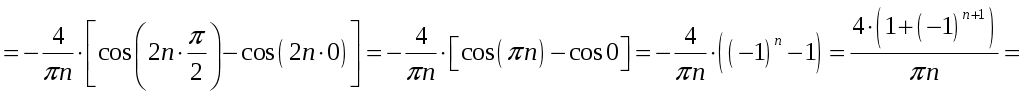
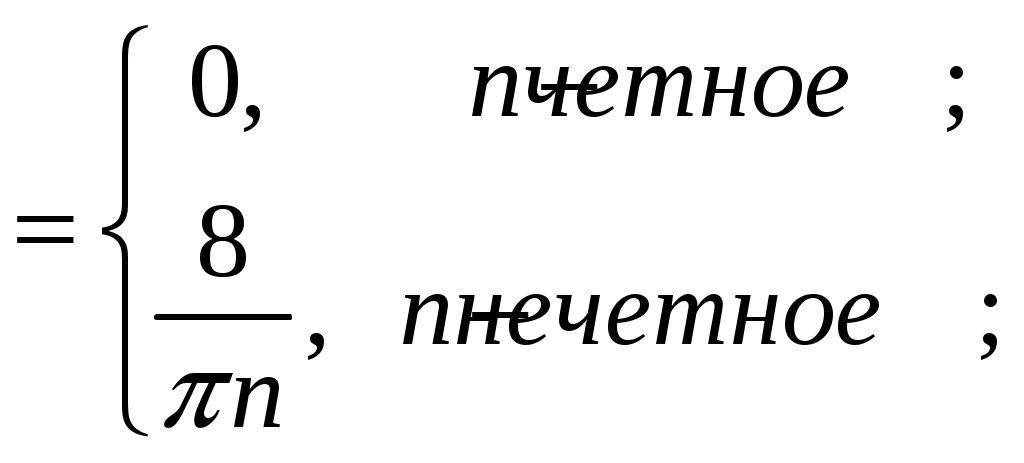 .
.Таким образом, для функции
2) В соответствии с теоремой Дирихле, график суммы ряда Фурье функции

3) Амплитуду ряда определяется по формуле
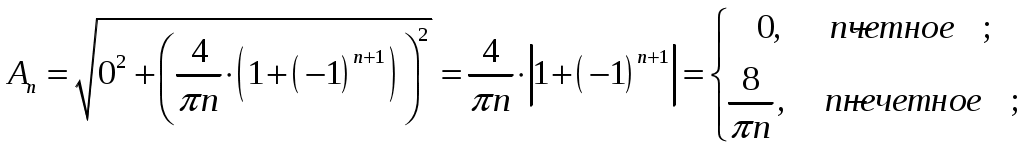 .
.Вычислим значения
при
при
при
при
при
.
Изображая амплитуды на диаграмме, получаем следующую картинку:
